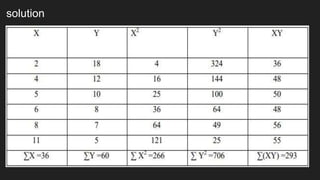
Karl Pearson’s coefficient measures the strength of a linear association between two variables, denoted as r, which ranges from -1 to +1. It indicates the direction and magnitude of the correlation, with +1 indicating a perfect positive correlation, -1 indicating a perfect negative correlation, and 0 indicating no relationship. The calculation of this coefficient requires certain assumptions, such as linearity between the variables and minimal outliers.

1. CORRELATION
KARL PEARSON’S COEFFICIENT CORRELATION

2. Intro
● Also called as “The Karl Pearson‘s product-moment correlation coefficient”.
● It is a measure of the strength of a linear association between two variables.
● denoted by r or rxy.
■ x and y being the two variables involved.
● It attempts to draw a line of best fit through the data of two variables.
● value of the Pearson correlation coefficient, r, indicates how far away all
these data points are to this line of best fit.
● r lies between -1 and +1, or –1 ≤ r ≤ 1, or the numerical value of r cannot
exceed one (unity).

3. Interpretation of r.
● The value of the coefficient of correlation will always lie between -1 and +1.,
i.e., –1 ≤ r ≤ 1.
○ If r = +1, it means, there is perfect positive correlation.
○ If r = -1, there is perfect negative correlation.
○ If r = 0, there is no relationship between the two variables.
● It describes not only the magnitude of correlation but also its direction.
■ The degree of correlation depends upon the value.
● + 0.1 shows Lower degree of +ve correlation
● +0.8 shows Higher degree of +ve correlation.
● -0.1 shows Lower degree of -ve correlation.
● -0.8 shows Higher degree of -ve correlation.

4. Assumptions
While calculating Karl Pearson Correlation
● There is a linear relationship (or any linear component of the relationship) between
the two variables.
● We keep Outliers either to a minimum or remove them entirely.
Properties of the Pearson’s Correlation Coefficient
1. r lies between -1 and +1, or –1 ≤ r ≤ 1, or the numerical value of r cannot exceed one.
2. The correlation coefficient is independent of the change of origin and scale.
3. Two independent variables are uncorrelated but the converse is not true.

5. Limitations
● It is not able to tell the difference between dependent variables and
independent variables.
● It will not give you any information about the slope of the line.
● It only tells you whether there is a relationship.

6. Formula

7. Example 1: calculate correlation coefficient for the following data:
Solution
● Calculate the sum total of x.
● Calculate the sum total of y.
● Find x2 and its sum total.
● Find y2 and its sum total.
● Calculate (x * y) and its sumtotal.
● Calculate n∑xy
● Then apply to the formula.
n= number of pairs
of scores/ number of
variables.
Here n = 6

8. solution

9. As r = -0.920, there is high degree of negative correlation.

10. ASSIGNMENT
1. CALCULATE THE CORRELATION OF GIVEN DATA.
THANK YOU