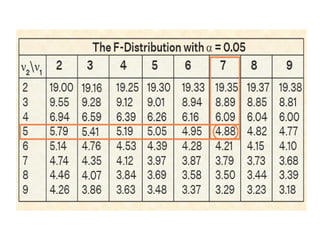
The document discusses the F test, which is used to compare the variances of two populations or samples to determine if they are equal. It defines the F test as the ratio of two independent chi-square variances divided by their respective degrees of freedom. The document provides the formula for the F test and describes the steps for conducting it, including stating the null and alternative hypotheses, calculating the F value, finding the critical value, and deciding whether to reject or fail to reject the null hypothesis. An example comparing the variances of drug test results before and after treatment is shown. Merits of the F test include its flexibility, while a limitation is that it works best with larger sample sizes.

1. Synopsis
Introduction
defination
Formula and methods
examples
Merit and demerit of F test
Conclusion
References

2. Introduction
F test is a statistical test that
is used in hypothesis testing
to check whether the
variances of two populations
or two samples are equal or
not. In an f test, the data
follows an f distribution. This
test uses the f statistic to
compare two variances by
dividing them

3. Defination
“F test is the ratio
of two
independent chi-
square variance
divided by their
respective degree
of freedom”

4. Formula

5. Methods
• State the null hypothesis
with the alternate
hypothesis.
• Calculate the F-value, using
the formula.
• Find the F Statistic which is
the critical value for this
test. ...
• Finally, support or reject the
Null Hypothesis.

6. Examples of F-test
• Example 1: A research team wants
to study the effects of a new drug
on insomnia. 8 tests were
conducted with a variance of 600
initially. After 7 months 6 tests
were conducted with a variance of
400. At a significance level of 0.05
was there any improvement in the
results after 7 months?

7. Solution
• : As the variance needs to be compared, the f test needs
to be used.
H0 : s21=s22
H1 : s21>s22
n1 = 8, n2 = 6
df1 = 8 - 1 = 7
df2 = 6 - 1 = 5
s21 = 600, s22 = 400
The f test formula is given as follows:
F = s21s22 = 600 / 400
F = 1.5
Now from the F table the critical value F(0.05, 7, 5) = 4.88

9. Answer
• As 1.5 < 4.88, thus, the null hypothesis
cannot be rejected and there is not enough
evidence to conclude that there was an
improvement in insomnia after using the new
drug.
Answer: Fail to reject the null hypothesis

10. Merits of F test
• F-tests are surprisingly flexible
because you can include
different variances in the ratio
to test a wide variety of
properties. F-tests can
compare the fits of different
models, test the overall
significance in regression
models, test specific terms in
linear models, and determine
whether a set of means are all
equal.

11. Demerits of F test
• A limitation of the t
test was that the
amount of data that
was provided was slim
and therefore Samples
of larger amount of
values would more
accurately represent
the population.

12. Conclusion & References
• The F-test of overall
significance is the
hypothesis test for this
relationship. If the overall
F-test is significant, you
can conclude that R-
squared does not equal
zero, and the correlation
between the model and
dependent variable is
statistically significant.