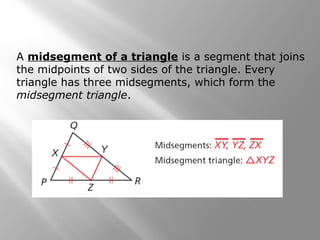
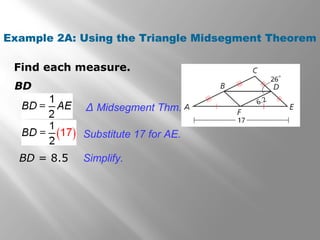
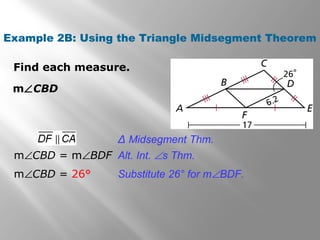
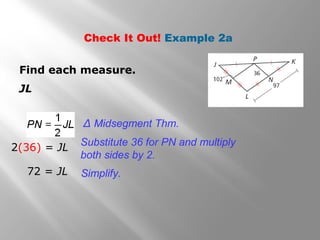
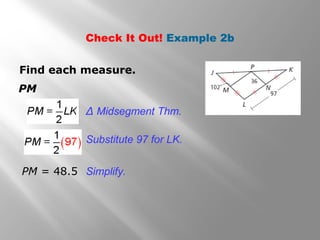
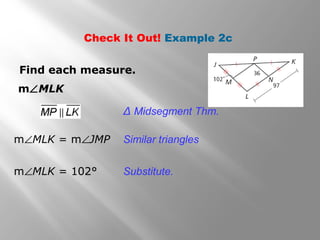
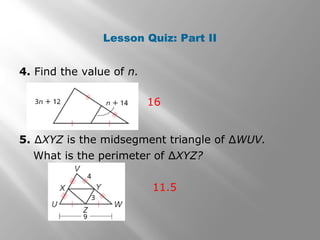
This document discusses properties of midsegments in triangles. It begins with examples calculating midpoints and midsegments. It then states that the three midsegments of any triangle form a new triangle called the midsegment triangle. Several examples demonstrate using the triangle midsegment theorem, which states that the length of a midsegment is equal to half the product of the lengths of the two sides divided by the midsegment. The document provides practice problems applying the theorem to find lengths and angle measures. It concludes with a lesson quiz involving additional midsegment problems.

1. UUNNIITT 55..11 MMIIDD--SSEEGGMMEENNTTSS OOFF
Holt Geometry
TTRRIIAANNGGLLEESS

2. Warm Up
Use the points A(2, 2), B(12, 2) and C(4, 8) for
Exercises 1–5.
1. Find X and Y, the midpoints of AC and CB.
2. Find XY.
3. Find AB.
4. Find the slope of AB.
5. Find the slope of XY.
6. What is the slope of a line parallel to
3x + 2y = 12?
(3, 5), (8, 5)
5
10
0
0

3. Objective
Prove and use properties of triangle
midsegments.

4. Vocabulary
midsegment of a triangle

5. A midsegment of a triangle is a segment that joins
the midpoints of two sides of the triangle. Every
triangle has three midsegments, which form the
midsegment triangle.

6. Example 1: Examining Midsegments in the
Coordinate Plane
The vertices of ΔXYZ are X(–1, 8), Y(9, 2), and
Z(3, –4). M and N are the midpoints of XZ and
YZ. Show that and .
Step 1 Find the coordinates of M and N.

7. Example 1 Continued
Step 2 Compare the slopes of MN and XY.
Since the slopes are the same,

8. Example 1 Continued
Step 3 Compare the heights of MN and XY.

9. Check It Out! Example 1
The vertices of ΔRST are R(–7, 0), S(–3, 6),
and T(9, 2). M is the midpoint of RT, and N is
the midpoint of ST. Show that and
Step 1 Find the coordinates of M and N.

10. Check It Out! Example 1 Continued
Step 2 Compare the slopes of MN and RS.
Since the slopes are equal .

11. Check It Out! Example 1 Continued
Step 3 Compare the heights of MN and RS.
The length of MN is half the length of RS.

12. The relationship shown in Example 1 is true for
the three midsegments of every triangle.

13. Example 2A: Using the Triangle Midsegment Theorem
Find each measure.
BD = 8.5
Δ Midsegment Thm.
Substitute 17 for AE.
Simplify.
BD

14. Example 2B: Using the Triangle Midsegment Theorem
Find each measure.
mÐCBD
Δ Midsegment Thm.
Alt. Int. Ðs Thm.
Substitute 26° for mÐBDF.
mÐCBD = mÐBDF
mÐCBD = 26°

15. Check It Out! Example 2a
Find each measure.
JL
Δ Midsegment Thm.
Substitute 36 for PN and multiply
both sides by 2.
Simplify.
2(36) = JL
72 = JL

16. Check It Out! Example 2b
Find each measure.
PM
Δ Midsegment Thm.
Substitute 97 for LK.
PM = 48.5 Simplify.

17. Check It Out! Example 2c
Find each measure.
mÐMLK
Δ Midsegment Thm.
Similar triangles
Substitute.
mÐMLK = mÐJMP
mÐMLK = 102°

18. Example 3: Indirect Measurement Application
In an A-frame support, the distance
PQ is 46 inches. What is the length
of the support ST if S and T are at
the midpoints of the sides?
Δ Midsegment Thm.
Substitute 46 for PQ.
ST = 23 Simplify.
The length of the support ST is 23 inches.

19. Check It Out! Example 3
What if…? Suppose Anna’s result in Example 3
(p. 323) is correct. To check it, she measures a
second triangle. How many meters will she
measure between H and F?
Δ Midsegment Thm.
Substitute 1550 for AE.
HF = 775 m Simplify.

20. Lesson Quiz: Part I
Use the diagram for Items 1–3. Find each
measure.
1. ED
10
2. AB
14
3. mÐBFE
44°

21. Lesson Quiz: Part II
4. Find the value of n.
16
5. ΔXYZ is the midsegment triangle of ΔWUV.
What is the perimeter of ΔXYZ?
11.5

22. All rights belong to their
respective owners.
Copyright Disclaimer Under
Section 107 of the
Copyright Act 1976,
allowance is made for "fair
use" for purposes such as
criticism, comment, news
reporting, TEACHING,
scholarship, and research.
Fair use is a use permitted
by copyright statute that
might otherwise be
infringing.
Non-profit, EDUCATIONAL
or personal use tips the
balance in favor of fair use.