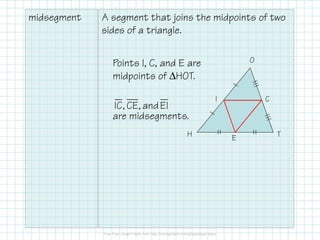
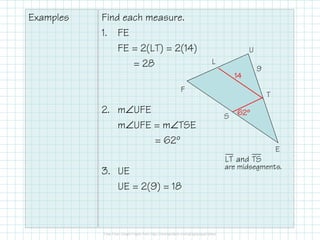
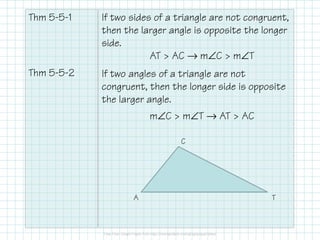
The document outlines key triangle theorems, including the midsegment theorem, which states a midsegment is parallel to a triangle's side and half its length. It discusses relationships between angles and side lengths, including the triangle inequality theorem, which asserts the sum of two sides must be greater than the third. Examples illustrate the application of these theorems in finding side lengths and angles.

1. Obj. 23 Triangle Theorems
The student is able to (I can):
• Identify a midsegment of a triangle and use it to solve
problems.
• Analyze the relationship between the angles of a triangle
and the lengths of the sides
• Determine allowable lengths for sides of triangles

2. midsegment
A segment that joins the midpoints of two
sides of a triangle.
O
Points I, C, and E are
midpoints of ∆HOT.
IC, CE, and EI
are midsegments.
H
I
C
E
T

3. Triangle Midsegment Theorem
A midsegment of a triangle is parallel to
a side of the triangle, and its length is
half the length of that side.
O
1
IC HT, IC = HT
2
H
I
C
E
T

4. Examples
Find each measure.
1. FE
FE = 2(LT) = 2(14)
= 28
U
L
14
9
F
2. m∠UFE
m∠UFE = m∠TSE
= 62º
T
S
62º
E
LT and TS
3. UE
UE = 2(9) = 18
are midsegments.

5. Thm 5-5-1
If two sides of a triangle are not congruent,
then the larger angle is opposite the longer
side.
AT > AC → m∠C > m∠T
Thm 5-5-2
If two angles of a triangle are not
congruent, then the longer side is opposite
the larger angle.
m∠C > m∠T → AT > AC
C
A
T

6. Triangle Inequality Theorem
The sum of any two side lengths of a
triangle is greater than the third side
length.
Example:
1. Which set of lengths forms a triangle?
4, 5, 10
7, 9, 12
4 + 5 < 10
7 + 9 > 12

7. Note: To find a range of possible third
sides given two sides, subtract for
the lower bound and add for the
upper bound.
Examples:
2. What is a possible third side for a
triangle with sides 8 and 14?
14 — 8 = 6 lower bound
14 + 8 = 22 upper bound
The third side can be between 6 and 22.

8. 3. What is the range of values for the
third side of a triangle with sides 11 and
19?
19 — 11 = 8
19 + 11 = 30
8 < x < 30
lower bound
upper bound