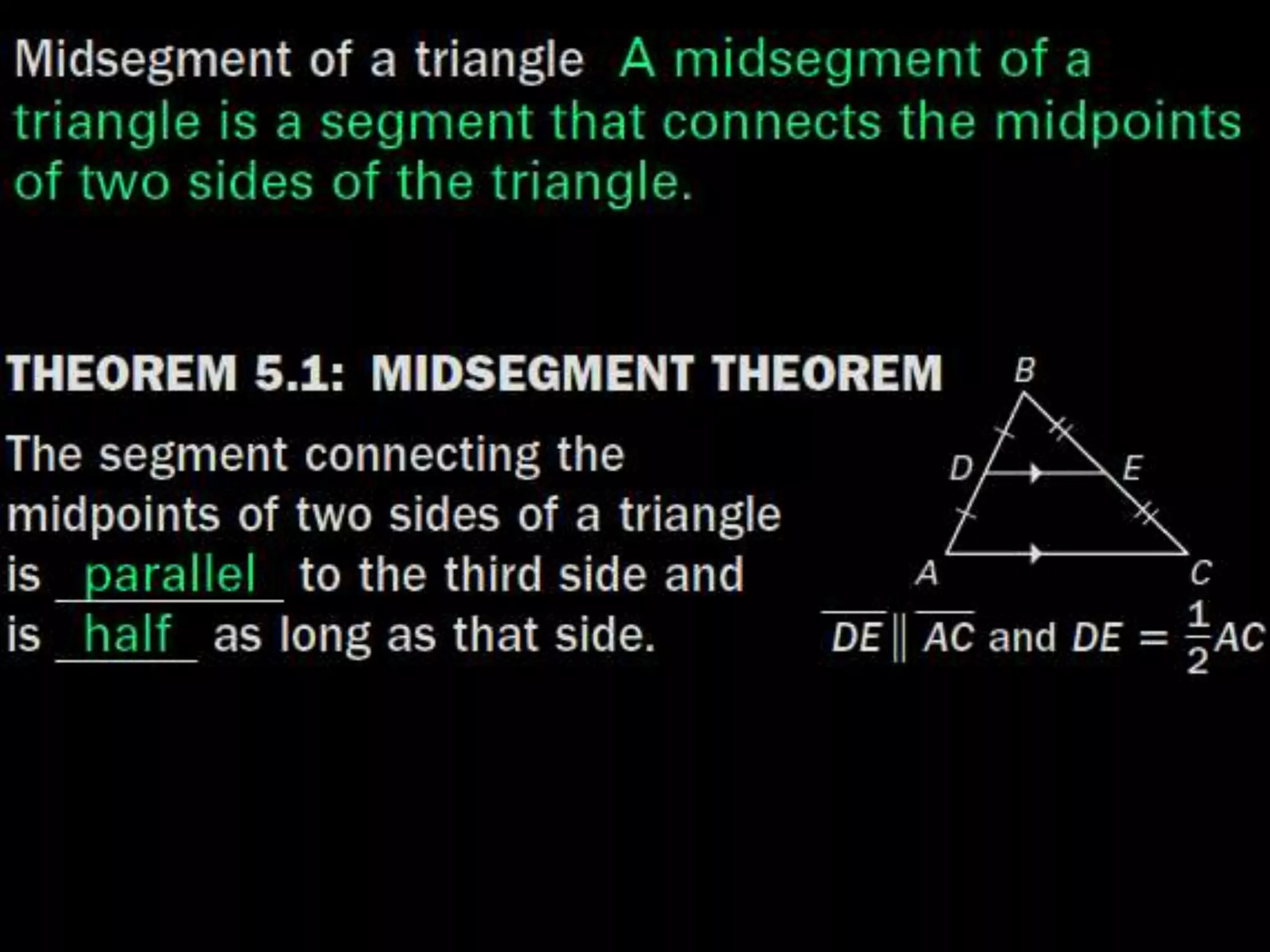
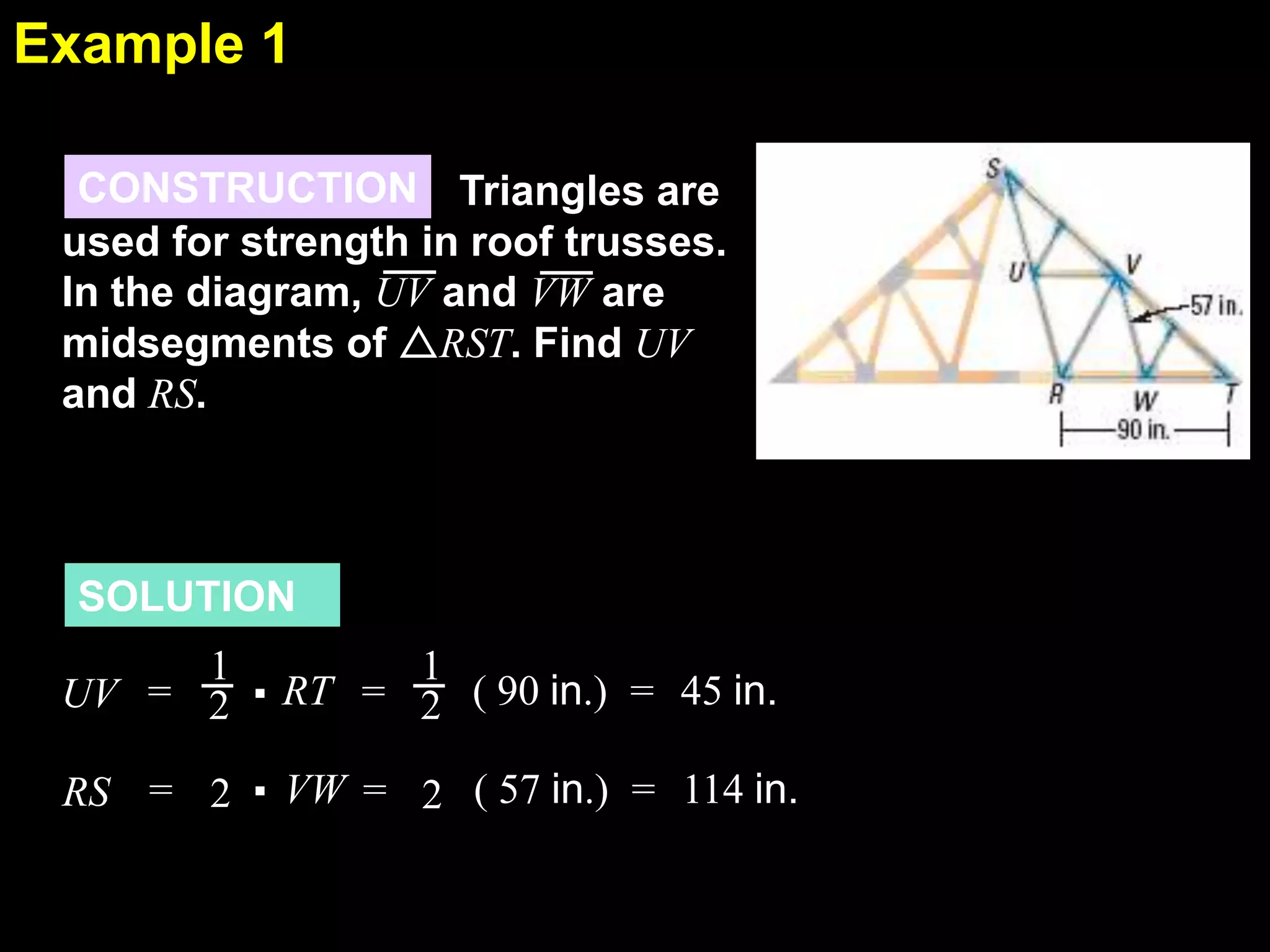
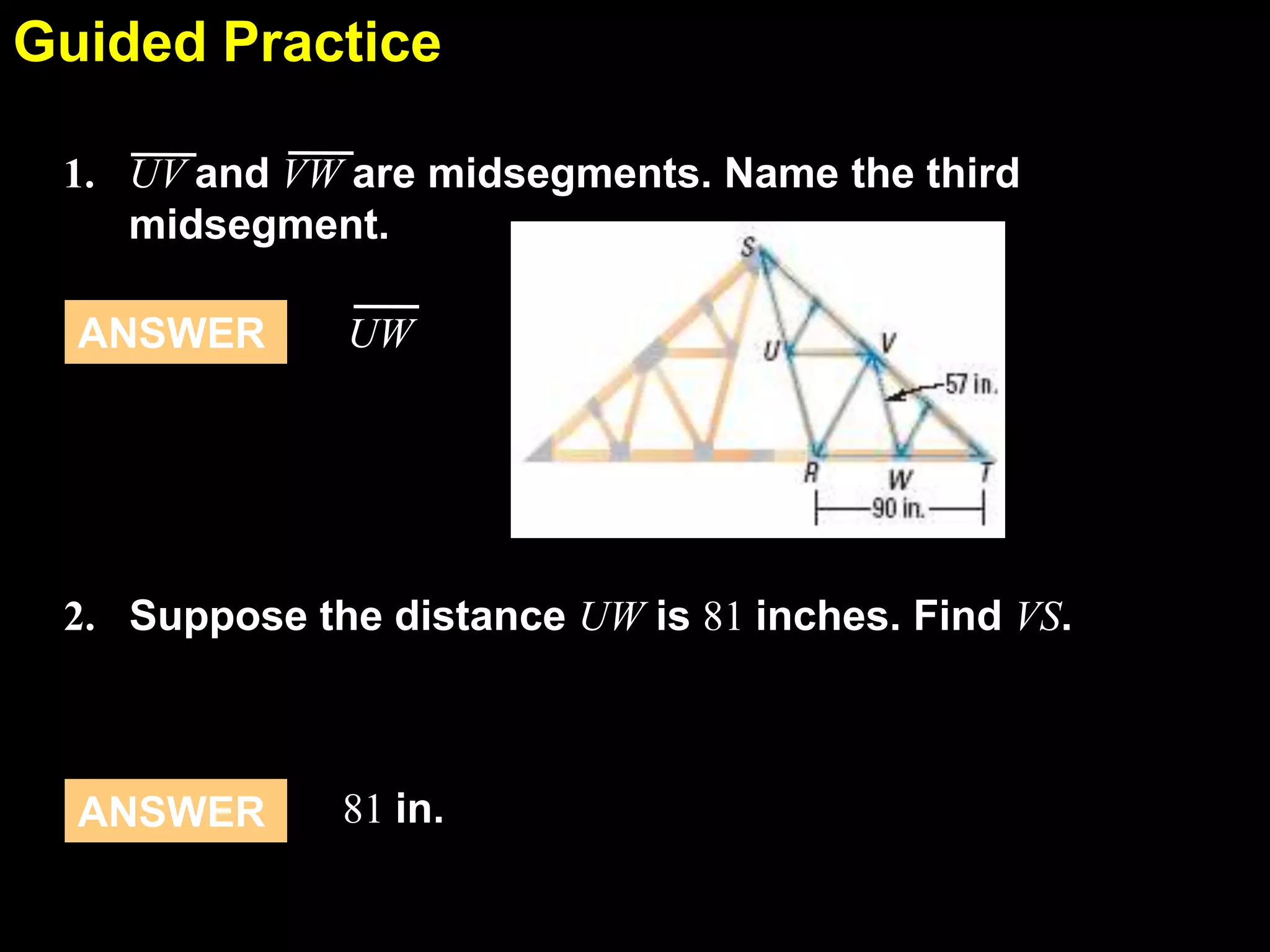
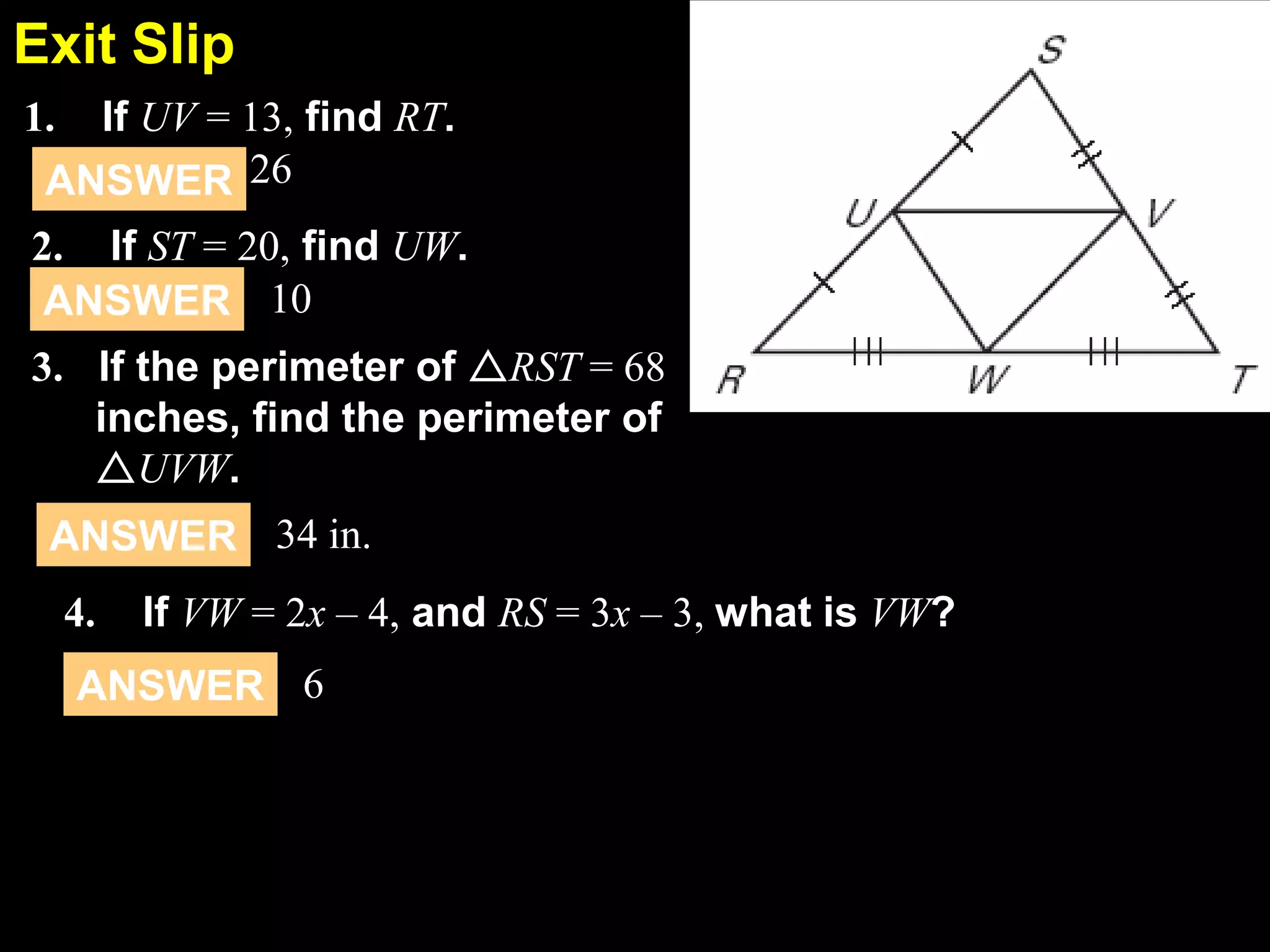
This document discusses using the midsegment theorem and coordinate proofs to find lengths and midpoints of line segments in triangles and rectangles. It provides examples of placing shapes like triangles and rectangles in a coordinate plane to find side lengths and midpoints using the distance and midpoint formulas. It also includes practice problems asking students to find side lengths, midpoints, and perimeters of shapes by using properties of midsegments or coordinates of vertices.

1. 5.1 Midsegment Theorem and Coordinate Proof
5.1
Bell Thinger
In Exercises 1– 4, use A(0, 10), B(24, 0), and C(0, 0).
1. Find AB.
ANSWER 26
2. Find the midpoint of CA.
ANSWER (0, 5)
3. Find the midpoint of AB.
ANSWER (12, 5)
4. Find the slope of AB.
– 5
ANSWER
12

2. 5.1

3. Example 1
5.1
CONSTRUCTION Triangles are
used for strength in roof trusses.
In the diagram, UV and VW are
midsegments of RST. Find UV
and RS.
SOLUTION
1
= 2
UV
. RT
1
= 2 ( 90 in.) = 45 in.
RS = 2
. VW =
2 ( 57 in.) = 114 in.

4. Guided Practice
5.1
1. UV and VW are midsegments. Name the third
midsegment.
ANSWER
UW
2. Suppose the distance UW is 81 inches. Find VS.
ANSWER
81 in.

5. Example 2
5.1
In the kaleidoscope image, AE ≅ BE
and AD ≅ CD . Show that CB DE .
SOLUTION
Because AE ≅ BE and AD ≅CD , E is the
midpoint of AB and D is the midpoint of
AC by definition.
Then DE is a midsegment of ABC by
definition and CB DE by the Midsegment
Theorem.

6. 5.1

7. Example 3
5.1
Place each figure in a coordinate plane in a way that
is convenient for finding side lengths. Assign
coordinates to each vertex.
a. Rectangle: length is h and width is k
b. Scalene triangle: one side length is d
SOLUTION
It is easy to find lengths of horizontal and vertical
segments and distances from (0, 0), so place one
vertex at the origin and one or more sides on an axis.

8. Example 3
5.1
a. Let h represent the length and k represent the width.
b. Notice that you need to use three different variables.

9. Guided Practice
5.1
3. Is it possible to find any of the side lengths
without using the Distance Formula? Explain.
ANSWER
Yes; the length of one
side is d.
4. A square has vertices (0, 0), (m, 0), and (0, m). Find
the fourth vertex.
ANSWER
(m, m)

10. Example 4
5.1
Place an isosceles right triangle in a coordinate
plane. Then find the length of the hypotenuse and the
coordinates of its midpoint M.
SOLUTION
Place PQO with the right angle
at the origin. Let the length of
the legs be k. Then the vertices
are located at P(0, k), Q(k, 0), and
O(0, 0).

11. Example 4
5.1
Use the Distance Formula to find PQ.
PQ =
2
2
(k – 0) + (0 – k) =
=
2
2
k + (– k) =
2
2k
= k
2
k +k
2
2
Use the Midpoint Formula to find the midpoint M of
the hypotenuse.
M( 0 + k , k + 0 ) = M( k , k )
2
2
2 2

12. Guided Practice
5.1
5. Graph the points O(0, 0), H(m, n), and J(m, 0).
Is
OHJ a right triangle? Find the side
lengths and the coordinates of the midpoint
of each side.
ANSWER
Sample:
yes; OJ = m, JH = n,
HO = m2 + n2,
m
n
OJ: ( 2 , 0), JH: (m, 2 ),
HO: ( m , n )
2
2

13. Exit Slip
5.1
If UV = 13, find RT.
ANSWER 26
1.
2. If ST = 20, find UW.
ANSWER 10
3. If the perimeter of RST = 68
inches, find the perimeter of
UVW.
ANSWER 34 in.
4.
If VW = 2x – 4, and RS = 3x – 3, what is VW?
ANSWER 6

14. Exit Slip
5.1
5.
Place a rectangle in a coordinate plane so its
vertical side has length a and its horizontal side
has width 2a. Label the coordinates of each
vertex.
ANSWER

15. 5.1
Homework
Pg 312-315
#27, 28, 29, 30, 35