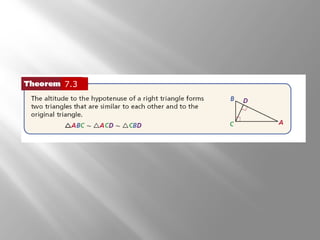
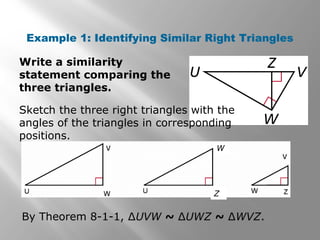
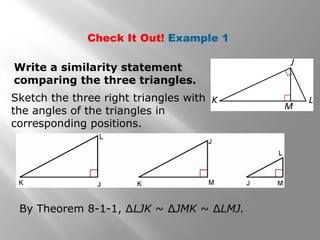
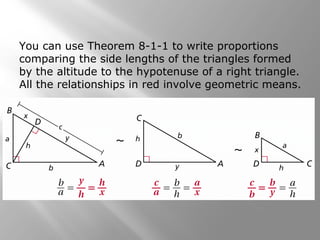
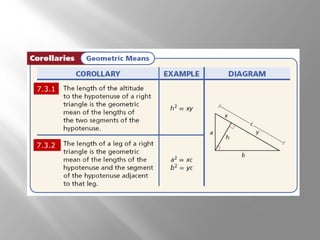
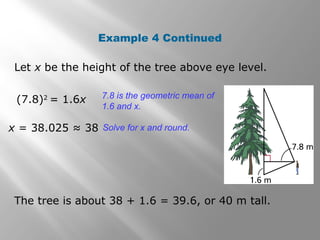
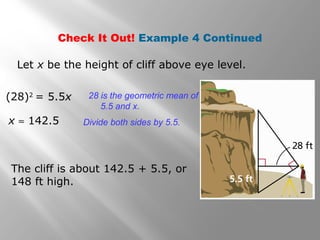
This document is from a geometry textbook and covers similarity in right triangles. It begins with objectives and vocabulary, then provides examples of identifying similar right triangles, finding geometric means, using geometric means to find unknown side lengths in right triangles, and an application to estimating height. Examples are included with step-by-step work shown. Students are then given a quiz to assess their understanding.

1. 7 UNIT 7..44 SSIIMMIILLAARRIITTYY IINN RRIIGGHHTT
Holt Geometry
TTRRIIAANNGGLLEESS

2. Warm Up
1. Write a similarity statement
comparing the two triangles.
ΔADB ~ ΔEDC
Simplify.
2. 3.
Solve each equation.
4. 5. 2x2 = 50
±5

3. Objectives
Use geometric mean to find segment
lengths in right triangles.
Apply similarity relationships in right
triangles to solve problems.

4. Vocabulary
geometric mean

5. In a right triangle, an altitude drawn from the
vertex of the right angle to the hypotenuse forms
two right triangles.

6. 7.3

7. Example 1: Identifying Similar Right Triangles
Write a similarity
statement comparing the
three triangles.
Sketch the three right triangles with the
angles of the triangles in corresponding
positions.
W
Z
By Theorem 8-1-1, ΔUVW ~ ΔUWZ ~ ΔWVZ.

8. Check It Out! Example 1
Write a similarity statement
comparing the three triangles.
Sketch the three right triangles with
the angles of the triangles in
corresponding positions.
By Theorem 8-1-1, ΔLJK ~ ΔJMK ~ ΔLMJ.

9. Consider the proportion . In this case, the
means of the proportion are the same number, and
that number is the geometric mean of the extremes.
The geometric mean of two positive numbers is the
positive square root of their product. So the geometric
mean of a and b is the positive number x such
that , or x2 = ab.

10. Example 2A: Finding Geometric Means
Find the geometric mean of each pair of
numbers. If necessary, give the answer in
simplest radical form.
4 and 25
Let x be the geometric mean.
x2 = (4)(25) = 100 Def. of geometric mean
x = 10 Find the positive square root.

11. Example 2B: Finding Geometric Means
Find the geometric mean of each pair of
numbers. If necessary, give the answer in
simplest radical form.
5 and 30
Let x be the geometric mean.
x2 = (5)(30) = 150 Def. of geometric mean
Find the positive square root.

12. Check It Out! Example 2a
Find the geometric mean of each pair of
numbers. If necessary, give the answer in
simplest radical form.
2 and 8
Let x be the geometric mean.
x2 = (2)(8) = 16 Def. of geometric mean
x = 4 Find the positive square root.

13. Check It Out! Example 2b
Find the geometric mean of each pair of
numbers. If necessary, give the answer in
simplest radical form.
10 and 30
Let x be the geometric mean.
x2 = (10)(30) = 300 Def. of geometric mean
Find the positive square root.

14. Check It Out! Example 2c
Find the geometric mean of each pair of
numbers. If necessary, give the answer in
simplest radical form.
8 and 9
Let x be the geometric mean.
x2 = (8)(9) = 72 Def. of geometric mean
Find the positive square root.

15. You can use Theorem 8-1-1 to write proportions
comparing the side lengths of the triangles formed
by the altitude to the hypotenuse of a right triangle.
All the relationships in red involve geometric means.

16. 7.3.1
7.3.2

17. Example 3: Finding Side Lengths in Right Triangles
Find x, y, and z.
62 = (9)(x) 6 is the geometric mean of
9 and x.
x = 4 Divide both sides by 9.
y2 = (4)(13) = 52 y is the geometric mean of
4 and 13.
Find the positive square root.
z2 = (9)(13) = 117 z is the geometric mean of
9 and 13.
Find the positive square root.

18. Helpful Hint
Once you’ve found the unknown side lengths,
you can use the Pythagorean Theorem to check
your answers.

19. Check It Out! Example 3
Find u, v, and w.
92 = (3)(u) 9 is the geometric mean of
u and 3.
u = 27 Divide both sides by 3.
w2 = (27 + 3)(27) w is the geometric mean of
u + 3 and 27.
Find the positive square root.
v2 = (27 + 3)(3) v is the geometric mean
of
Find the positivue + s 3q uaanrde 3ro. ot.

20. Example 4: Measurement Application
To estimate the height of a
Douglas fir, Jan positions
herself so that her lines of
sight to the top and bottom
of the tree form a 90º
angle. Her eyes are about
1.6 m above the ground,
and she is standing 7.8 m
from the tree. What is the
height of the tree to the
nearest meter?

21. Example 4 Continued
Let x be the height of the tree above eye level.
(7.8)2 = 1.6x
x = 38.025 ≈ 38
7.8 is the geometric mean of
1.6 and x.
Solve for x and round.
The tree is about 38 + 1.6 = 39.6, or 40 m tall.

22. Check It Out! Example 4
A surveyor positions himself
so that his line of sight to
the top of a cliff and his line
of sight to the bottom form
a right angle as shown.
What is the height of the
cliff to the nearest foot?

23. Check It Out! Example 4 Continued
Let x be the height of cliff above eye level.
(28)2 = 5.5x 28 is the geometric mean of
5.5 and x.
Divide x » 142.5 both sides by 5.5.
The cliff is about 142.5 + 5.5, or
148 ft high.

24. Lesson Quiz: Part I
Find the geometric mean of each pair of
numbers. If necessary, give the answer in
simplest radical form.
1. 8 and 18
12
2. 6 and 15

25. Lesson Quiz: Part II
For Items 3–6, use ΔRST.
3. Write a similarity statement comparing the
three triangles.
ΔRST ~ ΔRPS ~ ΔSPT
4
4. If PS = 6 and PT = 9, find PR.
5. If TP = 24 and PR = 6, find RS.
6. Complete the equation (ST)2 = (TP + PR)(?).
TP

26. All rights belong to their
respective owners.
Copyright Disclaimer Under
Section 107 of the
Copyright Act 1976,
allowance is made for "fair
use" for purposes such as
criticism, comment, news
reporting, TEACHING,
scholarship, and research.
Fair use is a use permitted
by copyright statute that
might otherwise be
infringing.
Non-profit, EDUCATIONAL
or personal use tips the
balance in favor of fair use.