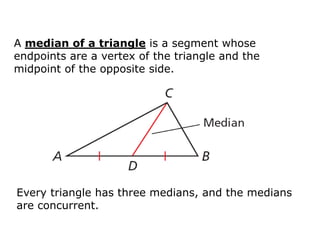
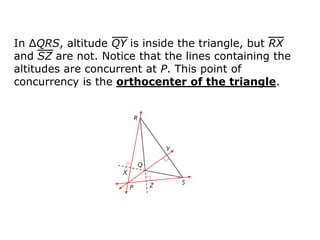
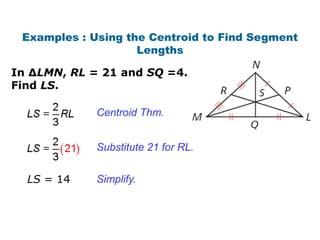
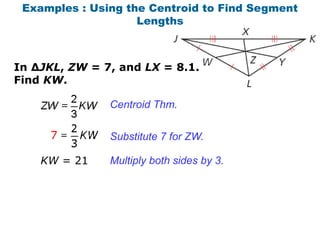
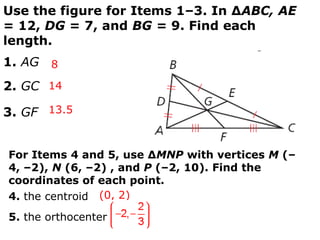
This geometry class covered properties of medians, altitudes, and centroids of triangles. Key points include: - The medians of a triangle are concurrent at the centroid. - The centroid is the point of concurrency of the medians and is always inside the triangle. - A triangle has three altitudes, which may be inside, outside, or on the triangle. The altitudes are concurrent at the orthocenter. - Examples demonstrated using the centroid theorem to find lengths of segments related to a triangle's medians. 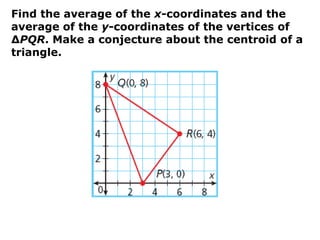- A conjecture was made that the x-coordinate of a triangle's centroid is the average of the x-coordinates of the vertices, and similarly for the y-coordinate.

1. GT Geometry 1/4/13
• Take out the piece of patty paper
from yesterday
• HW on the corner of your desk
• Pass out papers in bin!
• Midterm = 2 test grades

2. Objectives
Apply properties of medians of a
triangle.
Apply properties of altitudes of a
triangle.

3. Vocabulary
median of a triangle
centroid of a triangle
altitude of a triangle
orthocenter of a triangle

4. A median of a triangle is a segment whose
endpoints are a vertex of the triangle and the
midpoint of the opposite side.
Every triangle has three medians, and the medians
are concurrent.

5. The point of concurrency of the medians of a triangle
is the centroid of the triangle . The centroid is
always inside the triangle. The centroid is also called
the center of gravity because it is the point where a
triangular region will balance.

6. An altitude of a triangle is a perpendicular segment
from a vertex to the line containing the opposite side.
Every triangle has three altitudes. An altitude can be
inside, outside, or on the triangle.

7. In ΔQRS, altitude QY is inside the triangle, but RX
and SZ are not. Notice that the lines containing the
altitudes are concurrent at P. This point of
concurrency is the orthocenter of the triangle.

8. Helpful Hint
The height of a triangle is the length of an
altitude.

9. vocabulary
The midsegment of a
triangle - Segment that
joins the midpoints of
any two sides of a
triangle.

10. Triangle Midsegment

11. Theorem
The midsegment of a
triangle is half the
length of, and
parallel to, the third
side of a triangle.

12. GT Geometry
1. Turn in Cumulative Test on
the book shelf, by the time
the bell rings, nice neat pile.
2. Clear your desk of everything
but your geometric tools and
a pencil
3. Pass out papers in bin!

13. Examples : Using the Centroid to Find Segment
Lengths
In ∆LMN, RL = 21 and SQ =4.
Find LS.
Centroid Thm.
Substitute 21 for RL.
LS = 14 Simplify.

14. Examples : Using the Centroid to Find Segment
Lengths
In ∆LMN, RL = 21 and SQ =4.
Find NQ.
Centroid Thm.
NS + SQ = NQ Seg. Add. Post.
Substitute NQ for NS.
Subtract from both sides.
Substitute 4 for SQ.
12 = NQ Multiply both sides by 3.

15. Examples : Using the Centroid to Find Segment
Lengths
In ∆JKL, ZW = 7, and LX = 8.1.
Find KW.
Centroid Thm.
Substitute 7 for ZW.
KW = 21 Multiply both sides by 3.

16. Find the average of the x-coordinates and the
average of the y-coordinates of the vertices of
∆PQR. Make a conjecture about the centroid of a
triangle.

17. The x-coordinates are 0, 6 and 3. The average
is 3.
The y-coordinates are 8, 4 and 0. The average
is 4.
The x-coordinate of the centroid is the average
of the x-coordinates of the vertices of the
∆, and the y-coordinate of the centroid is the
average of the y-coordinates of the vertices of
the ∆.

18. Use the figure for Items 1–3. In ∆ABC, AE
= 12, DG = 7, and BG = 9. Find each
length.
1. AG 8
2. GC 14
3. GF 13.5
For Items 4 and 5, use ∆MNP with vertices M (–
4, –2), N (6, –2) , and P (–2, 10). Find the
coordinates of each point.
4. the centroid (0, 2)
5. the orthocenter