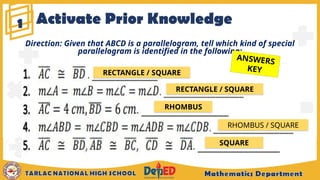
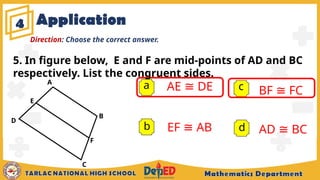
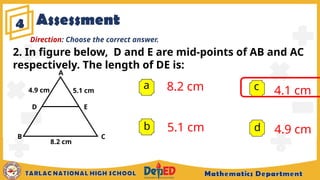
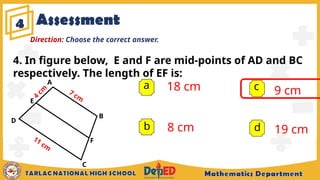
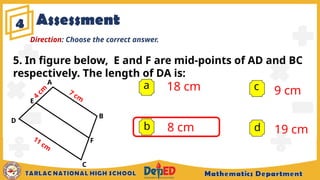
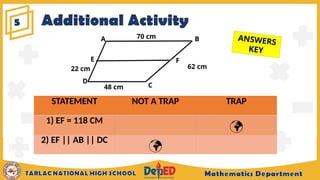
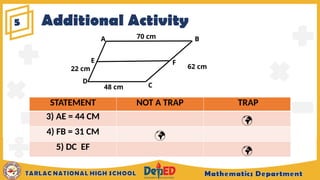
The document outlines the midline theorem for triangles and trapezoids, explaining its properties and how to apply it to solve problems involving these shapes. It includes illustrative examples and exercises aimed at grade 9 students, aiming to deepen their understanding of midlines, midsegments, and related geometric concepts. Additionally, it covers prior knowledge regarding special parallelograms and provides assessment questions to evaluate students' comprehension.

1. Grade 9
Third Quarter
MIDLINE
THEOREM
1
2
3
4
5
Lesson 4
Proves the Midline Theorem
(M9GEIIId-1)

2. OBJECTIVES
1
2
3
4
5
1. Illustrates the midline or
midsegment of a triangle and
trapezoid
2. Applies the Midline Theorem
3. Show accuracy in solving the
missing part of a triangle and a
trapezoid
Grade 9
Third Quarter
Lesson 4

3. Activate Prior Knowledge
1
Direction: Given that ABCD is a parallelogram, tell which kind of special
parallelogram is identified in the following:
SQUARE
RHOMBUS
RECTANGLE / SQUARE
RHOMBUS / SQUARE
RECTANGLE / SQUARE
ANSWERS
KEY

4. Acquire New Knowledge
2
THE MIDLINE THEOREM OF A TRIANGLE
In a triangle, a midline (or a midsegment) is any of the
three lines joining the midpoints of any pair of the
sides of the triangle.

5. Acquire New Knowledge
2
Illustration of the midlines that can be drawn in a triangle.
Note: The red segments are the midlines
C
B
A
C
B
A
C
A
B
Construction of a
midline in a
triangle
1. Find the
midpoints of
the two side
2. Connect the
midpoints.
Done!
The Midline Theorem in a Triangle suggests that the segment that joints
the midpoints of two sides of triangle is parallel to the third side and half as
long.

6. Acquire New Knowledge
2
C
A
B
The midline is PARALLEL to the third side
Illustration: Symbolism:
D E
>
>
DE || AC
Explanation:
This means the midline DE is
parallel to AC.
Note: Parallel line are marked with “feathers”. The
symbol “||” reads as “is parallel to”

7. Acquire New Knowledge
2
C
A
B
The midline is HALF AS LONG to the third side
Illustration: Symbolism:
D E
5 cm
DE = 1/2 AC or 2DE = AC
Explanation:
This means the midline is always half as
long as the third side (the parallel side to
it). In the same manner, the third side is
twice as long as the midline
10 cm

8. Acquire New Knowledge
2
Application of Theorem
• Midline Theorem will always work, on any triangle.
• It can use when looking other problems.
- Some Important Mathematical Ideas

9. Acquire New Knowledge
2
ILLUSTRATIVE EXAMPLE
In, O and I are the midpoints of CV
and VD, respectively. Consider each
given information and answer the
question that follow.
V
I
D
C
O

10. Acquire New Knowledge
2
ILLUSTRATIVE EXAMPLE
V
I
D
C
O
1. If OI = 18 CD = _____ How did you solve for CD?_________
OI = CD
18 = CD
2(18) = CD
36 = CD
CD = 36
Since OI is the midline, CD should
be twice as long. 18 multiplied by
2 is 36. therefore, CD = 36
18
?

11. Acquire New Knowledge
2
ILLUSTRATIVE EXAMPLE
V
I
D
C
O
2. If OC = 22.5 VC = _____ How did you solve for VC?_________
OC + OV = CV Since O is the midpoint of VC,
therefore OC and OV are equal
and by adding these two
segments, VC measures 45.
?
22.5
22.5 + 22.5 = CV
45= CV
CV = 45

12. Acquire New Knowledge
2
ILLUSTRATIVE EXAMPLE
V
I
D
C
O
3. If CD = 34 OI = _____ How did you solve for OI?_________
Since OI is the midline, it has to
be half of CD. 34 divided by 2 is
equal to 17. therefore, OI = 13
?
34
OI = CD
OI = (34)
OI = 17

13. Activate Prior Knowledge
2
Pass and Sing
1. Every rectangle is a square.
FALSE
2. Every square is a rectangle.
TRUE
3. Every square is a rhombus.
TRUE
4. Every rhombus is a square.
FALSE
5. The diagonals of a rhombus are perpendicular to each other.
TRUE

14. Activate Prior Knowledge
2
Pass and Sing
6. Every parallelogram is a square.
FALSE
7. Every square is a parallelogram.
TRUE
8. A rhombus is equiangular.
FALSE
9. If the diagonals of a given parallelogram are perpendicular, then the
parallelogram is a rectangle.
FALSE
10. A square is an equiangular and equilateral parallelogram.
TRUE

15. Acquire New Knowledge
2
Another kind of quadrilateral that is equally important as
parallelogram is the trapezoid and kite. A trapezoid is quadrilateral
with exactly one pair of parallel sides. The parallel side of a
trapezoid are called the bases and the non-parallel sides are called
legs. The angle formed by a base and a leg are called base angle.
You have to prove some theorems on trapezoids.
In a trapezoid, a midline (midsegment or median) is a line that joins
the midpoint of the sides that are not parallel
THE MIDLINE THEOREM OF A TRAPEZOID

16. Acquire New Knowledge
2
Illustration of the midline that can be drawn in a trapezoid.
Note: The red segments are the midlines.
The midline theorem in a trapezoid suggest that the segment
connecting the midpoints of the two legs of a trapezoid is parallel to the
bases, and its length is equal to half the sum of lengths of the bases.

17. Acquire New Knowledge
2
B
The midline is PARALLEL to the bases
Illustration: Symbolism:
Explanation:
This means that the midline
ED is parallel to the bases AB
and DC.
A
F
C
D
E
AB || EF , DC || EF

18. Acquire New Knowledge
2
• Midline Theorem will always work, on any trapezoid.
• It can use when looking other problems.
Application of Theorem
- Some Important Mathematical Ideas

19. Acquire New Knowledge
2
ILLUSTRATIVE EXAMPLE:
In Trapezoid LOVE, Y and U are
midpoints of LE and OV,
respectively. Consider each
given information and answer
the questions that follow.
E V
U
O
L
Y

20. Acquire New Knowledge
2
ILLUSTRATIVE EXAMPLE
1. If LO = 8 and VE = 6 YU = __ How did you solve for YU?______
Since YU is the midline, YU should
be half of the sum of the bases.
Half of the sum of 8 and 6 is 7.
Therefore YU = 7
YU =
E V
U
O
L
Y ?
8
YU =
YU =
YU = 7
6

21. Acquire New Knowledge
2
ILLUSTRATIVE EXAMPLE
2. If YU = 10 and LO = 13 VE = _____ How did you solve for VE?_______
Since YU is the midline, VE should
be obtain using the same
formula. Substitute the given,
multiplied both sides by 2,
transposed 13 and the result is 7.
Therefore, YU = 7
YU =
E V
U
O
L
Y 10
13
10 =
20 = 13 + VE
20 - 13 = VE
?
7 = VE
VE = 7

22. Acquire New Knowledge
2
ILLUSTRATIVE EXAMPLE:
L M
Q
N
O
P
If │PQ│= 20 cm,
│LM│ = x+3, and
│ON│ = x+6, what is
the value of x?

23. Acquire New Knowledge
2
ILLUSTRATIVE EXAMPLE:
L M
Q
N
O
P
If │LM│= 2x+2 cm,
│PQ│=3x+3, and
│ON│ = 2(x+6), what
is │LM│?

24. Application
3
a 48
24
6
12
b
c
d
Direction: Choose the correct answer.
E
D
1. In SIE, L and D are the midpoints of SI and IE
∆
respectively. If LD is 12, then what is the value of SE?
I
S
L

25. Application
3
a 28
21
7
14
b
c
d
Direction: Choose the correct answer.
E
D
2. In SIE, L and D are the midpoints of SI and IE
∆
respectively. If SE = 14, then what is the value of LD?
I
S
L

26. Application
3
a OU = BS
b
d
e
Direction: Choose the correct answer.
S
U
3. In BNS, O and U are the midpoints of BN and NS
∆
respectively. How will you compute the OU?
N
B
O
OU = US
OU = BN
OU = ON

27. Application
3
a BO ON
≅
b
c
d
Direction: Choose the correct answer.
S
U
4. In BNS, O and U are the midpoints of BN and NS
∆
respectively. List the congruent sides.
N
B
O
BO US
≅
ON UN
≅
NU US
≅

28. 4
a AE ≅ DE
EF ≅ AB
BF ≅ FC
AD ≅ BC
b
c
d
Direction: Choose the correct answer.
5. In figure below, E and F are mid-points of AD and BC
respectively. List the congruent sides.
A
B
C
D
F
E
Application

29. Assessment
4
a DE
IL
LS
SE
b
d
e
Direction: Choose the correct answer.
E
D
1. In figure below, D is mid-point of IE and LD|| SE then
ID is equal to
I
S
L

30. Assessment
4
a 8.2 cm
5.1 cm
4.1 cm
4.9 cm
b
c
d
Direction: Choose the correct answer.
2. In figure below, D and E are mid-points of AB and AC
respectively. The length of DE is:
A
B C
D E
4.9 cm 5.1 cm
8.2 cm

31. 3
a OU | | UN
b
c
d
Direction: Choose the correct answer.
S
U
3. In BNS, O and U are the midpoints of BN and NS
∆
respectively. List the parallel sides.
N
B
O
BO | | US
ON | | UN
OU | | BS
Assessment

32. Assessment
4
a 18 cm
8 cm
9 cm
19 cm
b
c
d
Direction: Choose the correct answer.
4. In figure below, E and F are mid-points of AD and BC
respectively. The length of EF is:
A
B
C
D
F
7 cm
11 cm
E
4
cm

33. Assessment
4
a 18 cm
8 cm
9 cm
19 cm
b
c
d
Direction: Choose the correct answer.
5. In figure below, E and F are mid-points of AD and BC
respectively. The length of DA is:
A
B
C
D
F
7 cm
11 cm
E
4
cm

34. Additional Activity
5
In trapezoid ABCD, EF is the midsegment. Apply your knowledge about
midsegment of a trapezoid by writing a check mark corresponding to the
statement whether it is NOT A TRAP for true statement, and TRAP for false
statement
A
E
D
B
F
C
22 cm
48 cm
70 cm
62 cm

35. Additional Activity
5
A
E
D
B
F
C
22 cm
48 cm
70 cm
62 cm
STATEMENT NOT A TRAP TRAP
1) EF = 118 CM

2) EF || AB || DC

ANSWERS
KEY

36. Additional Activity
5
A
E
D
B
F
C
22 cm
48 cm
70 cm
62 cm
STATEMENT NOT A TRAP TRAP
3) AE = 44 CM 
4) FB = 31 CM 
5) DC EF 

37. References
OTHER SUPPORTING LEARNING MATERIALS:
• Compendium of notes
• Instructional Support Materials In Mathematics
INTERNET:
• https://quizizz.com/admin/quiz/5df41634198380001bea369d/the-midli
e-theorem
• http://aven.amritalearning.com/index.php?sub=102&brch=305&sim=1
93&cnt=3871