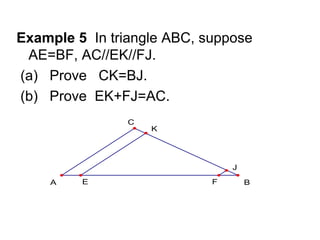
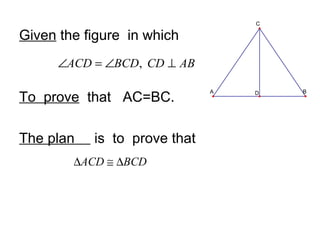
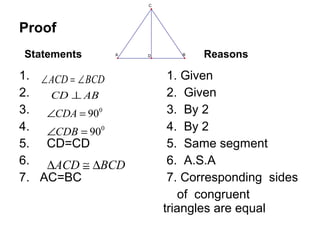
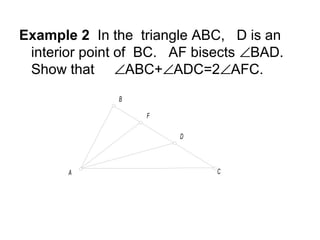
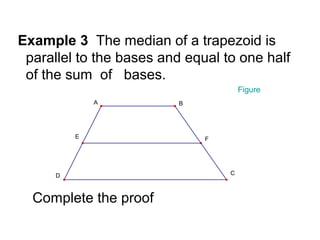
This document provides an outline and examples for proving theorems related to midpoints and intercepts in triangles. It includes: 1. Definitions of parallel lines, congruent triangles, and similar triangles. 2. Examples of proofs of the Triangle Midpoint Theorem - which states that the line segment connecting the midpoints of two sides of a triangle is parallel to the third side and half as long. 3. An example proof of the Triangle Intercept Theorem - which states that if a line is parallel to one side of a triangle, it divides the other two sides proportionally.

1. Chapter1: Triangle Midpoint Theorem
and Intercept Theorem
Outline
•Basic concepts and facts
•Proof and presentation
•Midpoint Theorem
•Intercept Theorem

2. 1.1. Basic concepts and facts
In-Class-Activity 1.
(a) State the definition of the following
terms:
Parallel lines,
Congruent triangles,
Similar triangles:

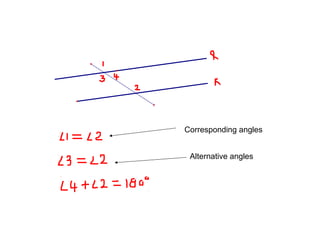
3. •Two lines are parallel if they do not meet
at any point
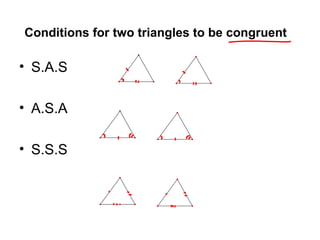
•Two triangles are congruent if their
corresponding angles and corresponding
sides equal
•Two triangles are similar if their
Corresponding angles equal and their
corresponding sides are in proportion.
[Figure1]

4. (b) List as many sufficient conditions as
possible for
• two lines to be parallel,
• two triangles to be congruent,
• two triangles to be similar

5. Conditions for lines two be parallel
• two lines perpendicular to the same line.
• two lines parallel to a third line
• If two lines are cut by a transversal ,
(a) two alternative interior (exterior) angles are
equal.
(b) two corresponding angles are equal
(c) two interior angles on the same side of
the transversal are supplement

6. Corresponding angles
Alternative angles

7. Conditions for two triangles to be congruent
• S.A.S
• A.S.A
• S.S.S

8. Conditions for two triangles similar
• Similar to the same triangle
• A.A
• S.A.S
• S.S.S

9. 1.2. Proofs and presentation
What is a proof? How to present a proof?
Example 1 Suppose in the figure ,
CD is a bisector of ∠ACB and CD
is perpendicular to AB. Prove AC is equal
to CB. C
A D B

10. C
Given the figure in which
∠ACD = ∠BCD, CD ⊥ AB
A B
To prove that AC=BC. D
The plan is to prove that
∆ACD ≅ ∆BCD

11. C
Proof
Statements A D B Reasons
1. ∠ ACD = ∠ BCD 1. Given
2. CD ⊥ AB 2. Given
3. ∠CDA = 900 3. By 2
4. ∠CDB = 900 4. By 2
5. CD=CD 5. Same segment
6. ∆ACD ≅ ∆BCD 6. A.S.A
7. AC=BC 7. Corresponding sides
of congruent
triangles are equal

12. Example 2 In the triangle ABC, D is an
interior point of BC. AF bisects ∠BAD.
Show that ∠ABC+∠ADC=2∠AFC.
B
F
D
A C

13. Given in Figure ∠BAF=∠DAF.
To prove ∠ABC+∠ADC=2∠AFC.
The plan is to use the properties of angles in
a triangle

14. Proof: (Another format of presenting a proof)
1. AF is a bisector of ∠BAD,
so ∠BAD=2∠BAF.
2. ∠AFC=∠ABC+∠BAF (Exterior angle )
3. ∠ADC=∠BAD+∠ABC (Exterior angle)
=2∠BAF +∠ABC (by 1)
4. ∠ADC+∠ABC
=2∠BAF +∠ABC+ ∠ABC ( by 3)
=2∠BAF +2∠ABC
=2(∠BAF +∠ABC)
=2∠AFC. (by 2)

15. What is a proof?
A proof is a sequence of statements,
where each statement is either
an assumption,
or a statement derived from the previous
statements ,
or an accepted statement.
The last statement in the sequence is the
conclusion.

16. 1.3. Midpoint Theorem
C
D E
A B
Figure2

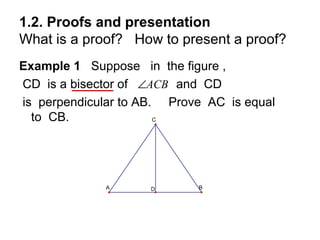
17. 1.3. Midpoint Theorem
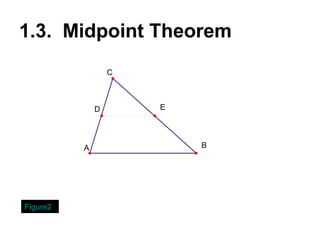
Theorem 1 [ Triangle Midpoint Theorem]
The line segment connecting the midpoints
of two sides of a triangle
is parallel to the third side
and
is half as long as the third side.

18. Given in the figure , AD=CD, BE=CE.
To prove DE// AB and DE= 2 AB 1
Plan: to prove ∆ACB ~ ∆DCE
C
D E
A B

19. Proof
Statements Reasons
1. ∠ACB = ∠DCE 1. Same angle
2. AC:DC=BC:EC=2 2. Given
4. ∆ACB ~ ∆DCE 4. S.A.S
5. ∠CAB = ∠CDE 5. Corresponding
angles of similar
triangles
6. corresponding angles
6. DE // AB
7. By 4 and 2
7. DE:AB=DC:CA=2
8. DE= 1/2AB 8. By 7.

20. In-Class Activity 2 (Generalization and
extension)
• If in the midpoint theorem we assume AD
and BE are one quarter of AC and BC
respectively, how should we change the
conclusions?
• State and prove a general theorem of
which the midpoint theorem is a special
case.

21. Example 3 The median of a trapezoid is
parallel to the bases and equal to one half
of the sum of bases.
Figure
A B
E F
D C
Complete the proof

22. Example 4 ( Right triangle median theorem)
The measure of the median on the
hypotenuse of a right triangle is one-half of
the measure of the hypotenuse.
B
E
C
A
Read the proof on the notes

23. In-Class-Activity 4
(posing the converse problem)
Suppose in a triangle the measure of a
median on a side is one-half of the measure
of that side. Is the triangle a right
triangle?

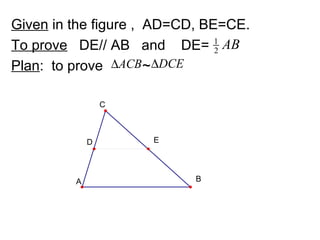
24. 1.4 Triangle Intercept Theorem
Theorem 2 [Triangle Intercept Theorem]
If a line is parallel to one side of a triangle
it divides the other two sides proportionally.
Also converse(?) . C
Figure
D E
Write down the complete A B
proof

25. Example 5 In triangle ABC, suppose
AE=BF, AC//EK//FJ.
(a) Prove CK=BJ.
(b) Prove EK+FJ=AC.
C
K
J
A E F B

26. (a)
1 KJ = EF
BJ BF
2. BK = BE
BJ BF
3. BE = CK
AE
BK
4. CK = BK
AE BE
5. CK = BF
AE
BJ
6. CK AE
=
BJ BF
=1
7. Ck=BJ
(b) Link the mid points of EF and KJ. Then use
the midline theorem for trapezoid

27. In-Class-Exercise
In ∆ABC, the points D and F are on side AB,
point E is on side AC.
(1) Suppose that
DE // BC , FE // DC , AF = 4, FD = 6
Draw the figure, then find DB.
( 2 ) Find DB if AF=a and FD=b.

28. Please submit the solutions of
(1) In –class-exercise on pg 7
(2) another 4 problems in
Tutorial 1
next time.
THANK YOU
Zhao Dongsheng
MME/NIE
Tel: 67903893
E-mail: dszhao@nie.edu.sg