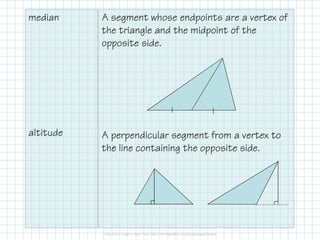
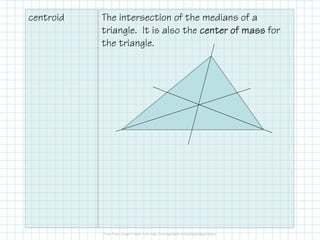
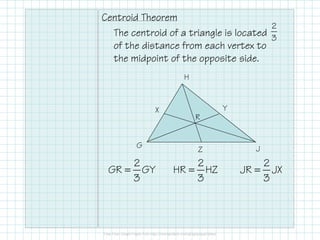
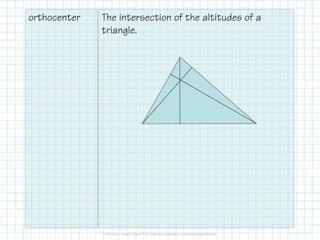
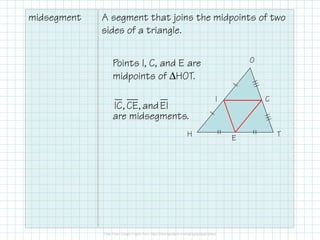
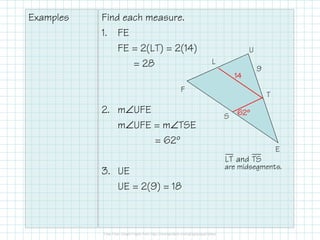
The document outlines concepts related to medians, altitudes, and midsegments in triangles, including definitions and theorems such as the centroid and orthocenter. It emphasizes the properties and relationships of these segments within triangles, providing examples and applications. Key learning objectives include identifying these segments and solving related problems.

1. Obj. 21 Medians, Altitudes, Midsegments
The student is able to (I can):
• Identify altitudes and medians of triangles
• Identify the orthocenter and centroid of a triangle
• Use triangle segments to solve problems
• Identify a midsegment of a triangle and use it to solve
problems.

2. median
altitude
A segment whose endpoints are a vertex of
the triangle and the midpoint of the
opposite side.
A perpendicular segment from a vertex to
the line containing the opposite side.

3. centroid The intersection of the medians of a
triangle. It is also the cccceeeennnntttteeeerrrr ooooffff mmmmaaaassssssss for
the triangle.

4. Centroid Theorem
The centroid of a triangle is located
of the distance from each vertex to
the midpoint of the opposite side.
G
H
J
X Y
R
Z
= 2
2
GR GY
3
= 2
HR HZ
3
JR JX
3
=
2
3

5. orthocenter The intersection of the altitudes of a
triangle.

6. midsegment A segment that joins the midpoints of two
sides of a triangle.
H
O
T
I C
E
Points I, C, and E are
midpoints of DHOT.
IC, CE, and EI
are midsegments.

7. Triangle Midsegment Theorem
A midsegment of a triangle is parallel to
a side of the triangle, and its length is
half the length of that side.
H
O
T
I C
E
1
IC HT, IC HT
2
=

8. Examples Find each measure.
1. FE
FE = 2(LT) = 2(14)
= 28
2. mÐUFE
F
mÐUFE = mÐTSE
= 62º
3. UE
UE = 2(9) = 18
L
U
T
E
S
14444
66662222º
9
LT and TS
are midsegments.