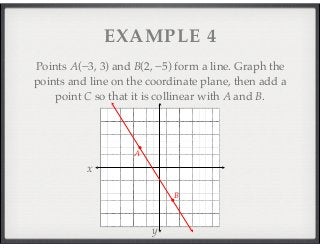
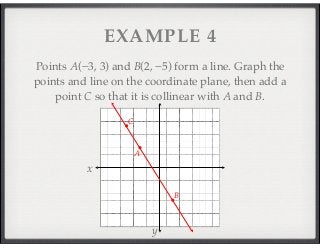
This document introduces key concepts in geometry including points, lines, planes, collinear points, coplanar points, and intersections. It defines points as having no size or shape, lines as infinite sets of points with no thickness, and planes as flat surfaces determined by three or more points that extend infinitely. Examples demonstrate identifying geometric objects from diagrams and real-world situations. Vocabulary and concepts are applied in problems identifying and relating points, lines and planes.

1. CHAPTER 1
Tools of Geometry

2. SECTION 1-1
Points, Lines, and Planes

3. ESSENTIAL QUESTIONS
How do you identify and model points, lines, and
planes?
How do you identify intersecting lines and planes?

4. VOCABULARY
1. Undefined Term:
2. Point:
3. Line:

5. VOCABULARY
1. U n d e fi n e d T e r m : The things in Geometry that can
really only be explained in examples and
descriptions
2. Point:
3. Line:

6. VOCABULARY
1. U n d e fi n e d T e r m : The things in Geometry that can
really only be explained in examples and
descriptions
2. P o i n t : A location in space with no shape or size;
noted as a capital letter
3. Line:

7. VOCABULARY
1. U n d e fi n e d T e r m : The things in Geometry that can
really only be explained in examples and
descriptions
2. P o i n t : A location in space with no shape or size;
noted as a capital letter
3. L i n e : An infinite number of points that together have
no thickness or width; need two points to determine
the line; use either a lowercase letter or AB

8. VOCABULARY
4. Plane:
5. Collinear:
6. Coplanar:
7. Intersection:

9. VOCABULARY
4. P l a n e : A flat surface with at least three points that
goes on forever in all directions; three points
determine a plane; Often a capital script letter
5. Collinear:
6. Coplanar:
7. Intersection:

10. VOCABULARY
4. P l a n e : A flat surface with at least three points that
goes on forever in all directions; three points
determine a plane; Often a capital script letter
5. C o l l i n e a r : Points that lie on the same line
6. Coplanar:
7. Intersection:

11. VOCABULARY
4. P l a n e : A flat surface with at least three points that
goes on forever in all directions; three points
determine a plane; Often a capital script letter
5. C o l l i n e a r : Points that lie on the same line
6. C o p l a n a r : Points that lie in the same plane
7. Intersection:

12. VOCABULARY
4. P l a n e : A flat surface with at least three points that
goes on forever in all directions; three points
determine a plane; Often a capital script letter
5. C o l l i n e a r : Points that lie on the same line
6. C o p l a n a r : Points that lie in the same plane
7. I n t e r s e c t i o n : Where two figures meet; this is the set
of points they have in common

13. VOCABULARY
8. Definition:
9. Defined Terms:
10. Space:

14. VOCABULARY
8. D e fi n i t i o n : Explanations that are used based off of
other undefined and defined terms
9. Defined Terms:
10. Space:

15. VOCABULARY
8. D e fi n i t i o n : Explanations that are used based off of
other undefined and defined terms
9. D e fi n e d T e r m s : Another way of working with a
definition
10. S p a c e : An infinite three-dimensional set of points

16. EXAMPLE 1
Use the figure to name each of the following.
a. A line containing point R
b. A plane containing point P

17. EXAMPLE 1
Use the figure to name each of the following.
a. A line containing point R
m, RT, RS, etc.
b. A plane containing point P

18. EXAMPLE 1
Use the figure to name each of the following.
a. A line containing point R
m, RT, RS, etc.
b. A plane containing point P
A

19. EXAMPLE 2
Name the geometric shape modeled by each object.
a. A crack in a sidewalk
b. A drop of water on the sidewalk

20. EXAMPLE 2
Name the geometric shape modeled by each object.
a. A crack in a sidewalk
line
b. A drop of water on the sidewalk

21. EXAMPLE 2
Name the geometric shape modeled by each object.
a. A crack in a sidewalk
line
b. A drop of water on the sidewalk
point

22. EXAMPLE 3
Draw and label plane T that contains lines UV and
WX such that the lines intersect at point Z. Then,
add a point H to plane T so that it is not collinear
with either UV or WX.

23. EXAMPLE 3
Draw and label plane T that contains lines UV and
WX such that the lines intersect at point Z. Then,
add a point H to plane T so that it is not collinear
with either UV or WX.
Compare your drawings with a neighbor; discuss

24. EXAMPLE 4
Points A(−3, 3) and B(2, −5) form a line. Graph the
points and line on the coordinate plane, then add a
point C so that it is collinear with A and B.

25. EXAMPLE 4
Points A(−3, 3) and B(2, −5) form a line. Graph the
points and line on the coordinate plane, then add a
point C so that it is collinear with A and B.

26. EXAMPLE 4
Points A(−3, 3) and B(2, −5) form a line. Graph the
points and line on the coordinate plane, then add a
point C so that it is collinear with A and B.
x
y

27. EXAMPLE 4
Points A(−3, 3) and B(2, −5) form a line. Graph the
points and line on the coordinate plane, then add a
point C so that it is collinear with A and B.
x
y
A

28. EXAMPLE 4
Points A(−3, 3) and B(2, −5) form a line. Graph the
points and line on the coordinate plane, then add a
point C so that it is collinear with A and B.
x
y
A
B

29. EXAMPLE 4
Points A(−3, 3) and B(2, −5) form a line. Graph the
points and line on the coordinate plane, then add a
point C so that it is collinear with A and B.
x
y
A
B

30. EXAMPLE 4
Points A(−3, 3) and B(2, −5) form a line. Graph the
points and line on the coordinate plane, then add a
point C so that it is collinear with A and B.
x
y
A
B
C

31. EXAMPLE 5
Answer the following.
a. How many points are need to form a line?
b. How many points are needed to form a plane?
c. What is the intersection of two planes?
d. What is the intersection of two lines?
e. What is the difference between collinear and coplanar?

32. PROBLEM SET

33. PROBLEM SET
p. 8 #1-47 odd, 58
“In terms of being late or not starting at all, then it’s
never too late.” - Alison Headley