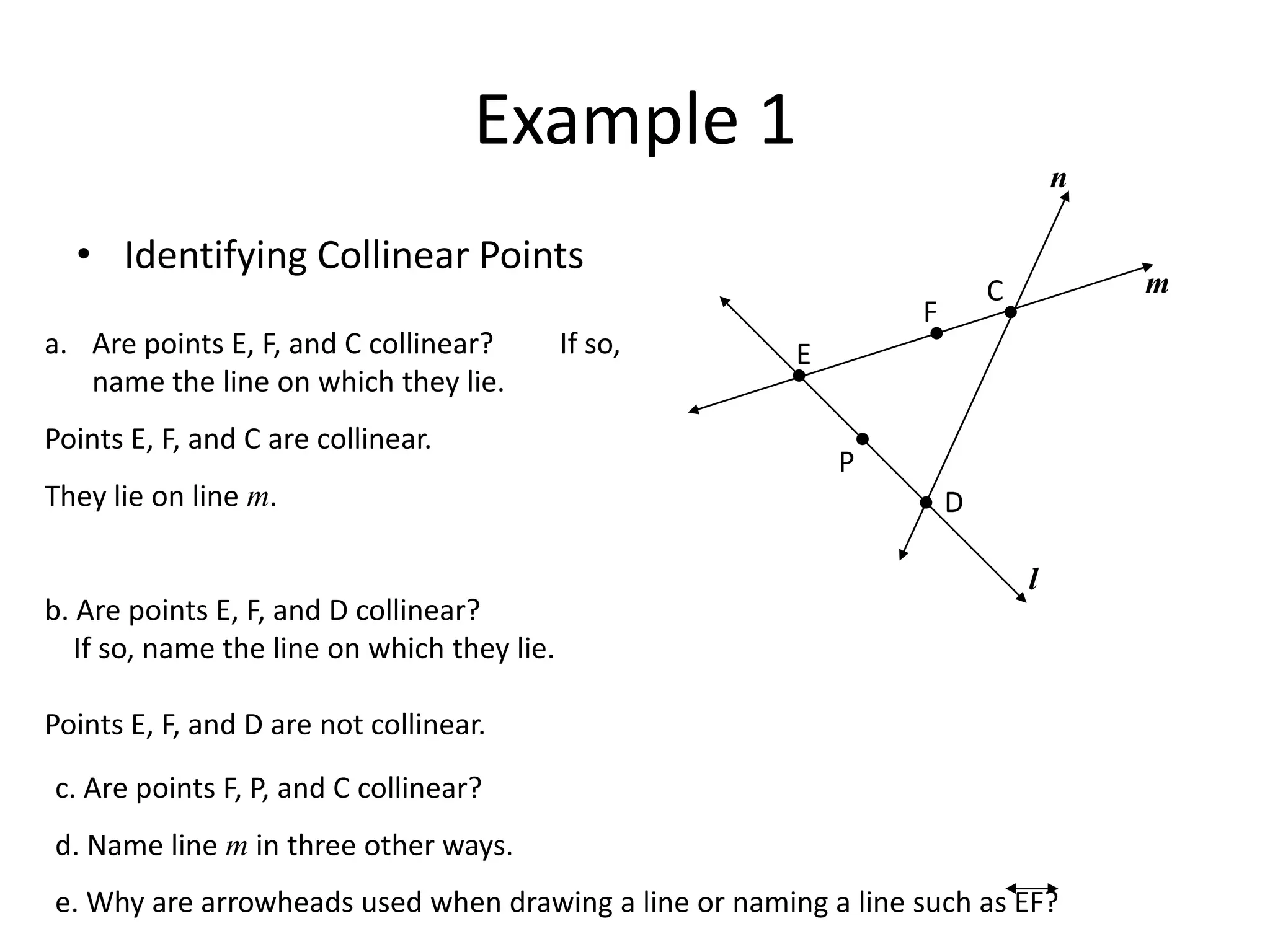
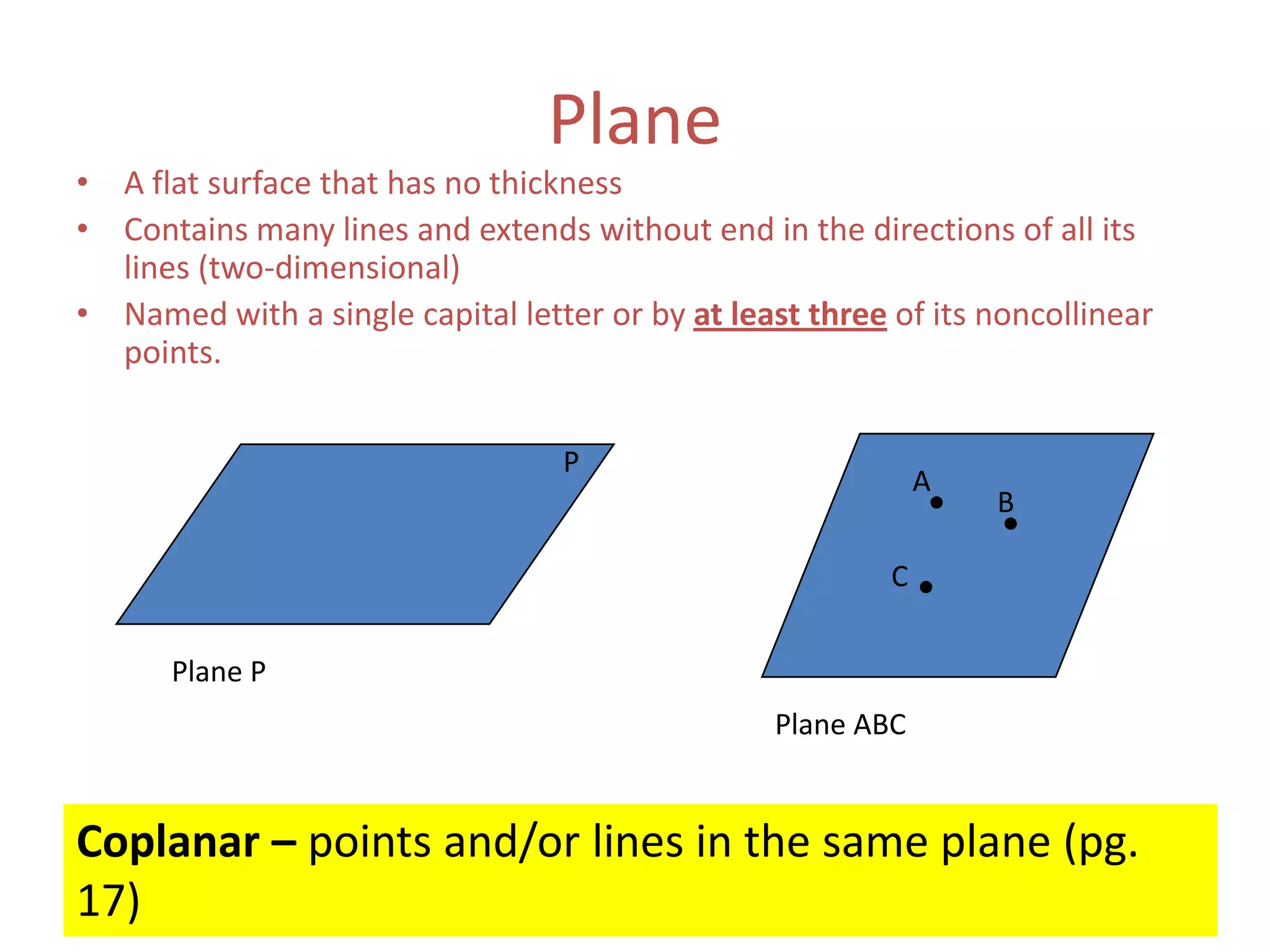
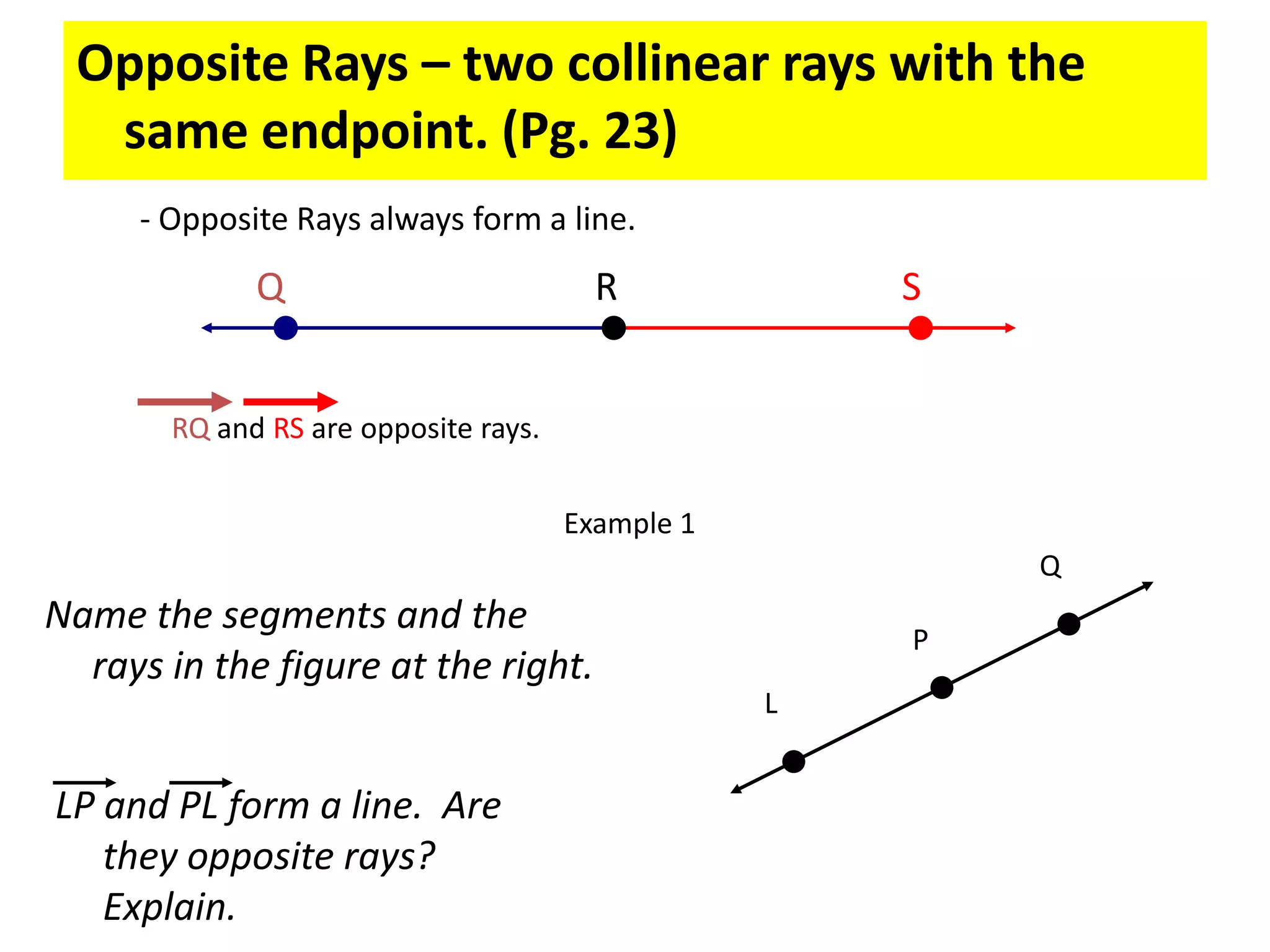
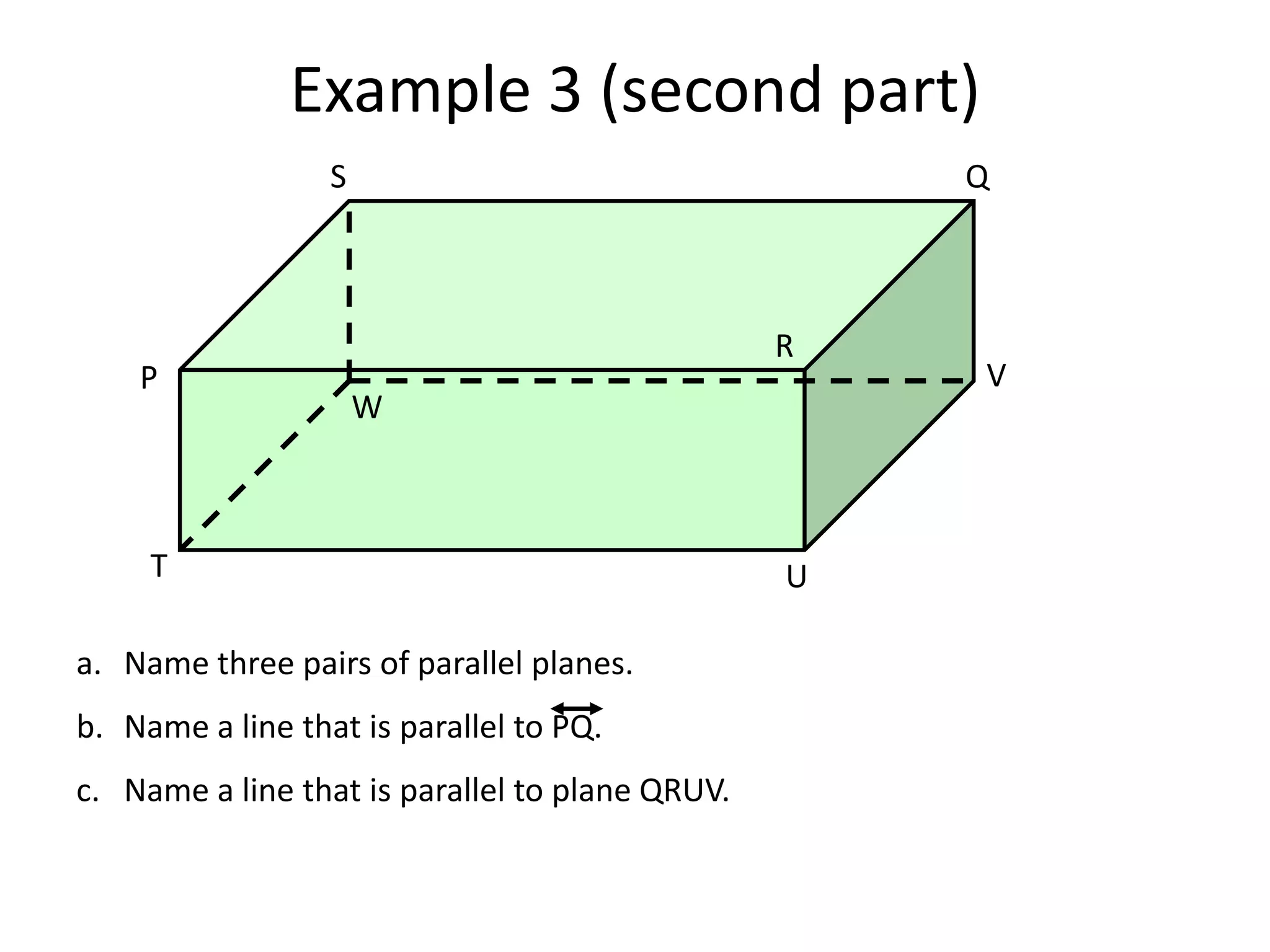
This document provides definitions and examples related to basic geometric terms including points, lines, rays, segments, planes, and parallelism. It defines points as having no size or dimensions, lines as extending in two directions, rays as extending from an endpoint, segments as being between two endpoints, and planes as flat surfaces that extend indefinitely. Examples are provided to demonstrate naming and identifying these terms as well as parallel and intersecting lines and planes. The document also introduces basic postulates about how these terms relate, such as two points defining a single unique line or three non-collinear points defining a single unique plane. Homework problems are assigned from the textbook.

1. Unit 1 – Section 2Points, Lines, Rays and Planes

2. Section 1-3: Points, Lines, & PlanesThe student will: - understand basic terms of geometry undefined (general description) defined - name points, lines, and planes - understand basic postulates of geometry including what a postulate isMaterials Needed: Definition Sheets, Postulate Sheets, Notes, Textbook, & a writing utensil

3. In geometry, some words such as point, line, and plane are undefined. In order to define these words you need to use words that need further defining. It is important, however, to have general descriptions of their meaning.

4. PointAA locationHas no size (no dimensions)Represented by a dotNamed with a capital letterA set of points can form a geometric figureBDCSpace – the set of all points (pg. 17)

5. LineA series of points that extends in two opposite directions without end (one-dimensional)Can be named by any two points on the line or with a single lowercase letterRSTYtRS (read “line RS”) orSY (read “line SY”) orTR (read “line TR”) & moreline t (read “line t”)Collinear Points – points that lie on the same line (pg. 17)

6. Example 1nIdentifying Collinear PointsmCFAre points E, F, and C collinear? If so, name the line on which they lie.Points E, F, and C are collinear.They lie on line m.b. Are points E, F, and D collinear? If so, name the line on which they lie.Points E, F, and D are not collinear.EPDlc. Are points F, P, and C collinear?d. Name line m in three other ways.e. Why are arrowheads used when drawing a line or naming a line such as EF?

7. PlaneA flat surface that has no thicknessContains many lines and extends without end in the directions of all its lines (two-dimensional)Named with a single capital letter or by at least three of its noncollinear points.PABCPlane PPlane ABCCoplanar – points and/or lines in the same plane (pg. 17)

8. Example 2Naming a PlaneHGHow many flat surfaces does the box (icecube) have?front back top bottom right side left sideEach one of these flat surfaces lies in a different plane.EFDCABList three different names for the plane represented by the top of the box (ice cube). List three different names for the plane represented by the right side of the box (ice cube.)

9. Postulate – an accepted statement of fact (pg. 18)Postulate 1-1 (Pg. 18)Through any two points there is exactly one line.BtALine t is the only line that passes through points A and B.Postulate 1-2 (Pg. 18)If two lines intersect, then they intersect in exactly one point.ABC AE and BD intersect at C.ED

10. Postulate 1-3 (Pg. 18)If two planes intersect, then they intersect in exactly one line.What points are in the purple plane? R, S, & TName the purple plane. Plane RSTWhat points are in the blue plane? S, T, & WName the blue plane. Plane STWWhat points are in both planes? S & TName the intersection of the two planes.RSWTPlane RST and plane STW intersect in ST.When you have two points that both lie in two different planes, the line through those two points is the intersection of the planes.

11. Example 3Finding the Intersection of two planes.What is the intersection of plane HGFE and plane BCGF?Plane HGFE and plane BCGF intersect in GF .HGEFDCABName two planes that intersect in BF.What is the intersection of plane ABFE and plane AEHD?

12. Postulate 1-4 (Pg. 19)Through any three noncollinear points there is exactly one plane. Example 4HGHGEEFFDCDCAABBa. Shade the plane that contains A, B, and C.b. Shade the plane that contains E, H, & C.c. Name another point that is in the same plane as points A, B, and C.d. Name another point that is coplanar with points E, H, and C.

13. Section 1-4: Segments, Rays, Parallel Lines & PlanesThe student will: - identify and name segments and rays - identify and name parallel lines and skew lines - identify and name parallel planesMaterials Needed: Definition Sheets, Notes, & a Writing Utensil

14. Many geometric figures, such as squares and angles, are formed by parts of lines called segments or rays.Segment – the part of a line consisting of two endpoints and all points between them. (Pg. 23) - a segment is named using its two endpoints - always use segment notation when naming segmentsBAAB (read “Segment AB”) or BA (read “Segment BA”)Are these two names for the same segment?

15. Ray – the part of a line consisting of one endpoint and all the points of the line on one side of the endpoint. (Pg. 23) - a ray is named with its endpoint (always listed first) and any other point on the ray - always use ray notation when naming raysYYXXYX (read “ray YX”) is the ray that starts at Y and then passes though X and continues on in that same direction without end.XY (read “ray XY”) is the ray that starts at X and then passes though Y and continues on in that same direction without end.Are these two names for the same ray?

16. Opposite Rays – two collinear rays with the same endpoint. (Pg. 23)- Opposite Rays always form a line.QRSRQ and RS are opposite rays.Example 1QName the segments and the rays in the figure at the right.PLLP and PL form a line. Are they opposite rays? Explain.

17. Lines that do not intersect may or may not be coplanar.Parallel Lines – coplanar lines that do not intersect. (Pg. 24) is the symbol for parallelSkew Lines – noncoplanar lines; they are not parallel and they do not intersect (Pg. 24)DCAB|| EFABAB& CGare skew.GHClassify AB and HG.Because I can draw a single plane that contains both of these lines, AB || HG.EF

18. Segments or rays are parallel if they lie in parallel lines. They are skew if they lie in skew lines.Example 2Name all labeled segments that are parallel to DC.BAGH, JI, & AB are parallel to DC.CDNGHName all labeled segments that are skew to DC.NJ, JG, & HI are skew to DC.JIName all labeled segments that are parallel to GJ.Name all labeled segments that are skew to GJ.Name another pair of parallel segments; of skew segments.

19. Parallel planes are planes that do not intersect. (Pg. 24)GHBIAJDCPlane ABCD || Plane GHIJWhat other planes in this figure are parallel?

20. Example 3 (second part)SQRVPWTUName three pairs of parallel planes.Name a line that is parallel to PQ.Name a line that is parallel to plane QRUV.

21. Homeworkp.19 #9-13 odd, 19,23,27,31,35,39,43p. 25 #1-7 odd, 13-21 odd, 27-33 oddBe sure to use proper notation on your answers.Additional Informationp. 25#7 – has 3 answers #17-21 – if false, be sure to explain!

22. ReferenceLaurie E. Bass, A. J. (2009). Geometry. Upper Saddle River, New Jersey: Pearson Education.