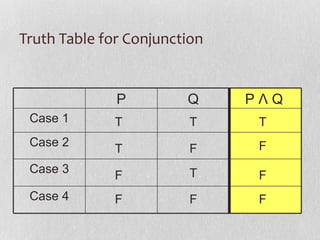
The document discusses truth tables, which are used to determine if compound statements are true or false. It provides examples of truth tables for negation, conjunction, and disjunction. A conjunction is true only when both statements are true, while a disjunction is true when at least one statement is true. Truth tables can have more than two statements, with each additional statement doubling the number of possible cases.

1. College Math SECTION 3.2: TRUTH TABLES FOR NEGATION, CONJUNCTION, AND DISJUNCTION

2. Truth Tables A truth table is used to determine when a compound statement is true or false. They are used to break a complicated compound statement into simple, easier to understand parts.

3. Truth Table for Negation As you can see “P” is a true statement then its negation “~P” or “not P” is false. If “P” is false, then “~P” is true. P T T F F ~P Case 1 Case 2

4. Four Possible Cases When a compound statement involves two simple statements P and Q, there are four possible cases for the combined truth values of P and Q. T T T T F F F F P Q Case 1 Case 2 Case 3 Case 4

5. When is a Conjunction True? Suppose I tell the class, “You can retake the last exam and you can turn in this lab late.” Let P be “You can retake the last exam” and Q be “You can turn in this lab late.” Which truth values for P and Q make it so that I kept my promise, P Λ Q to the class?

6. When is a Conjunction True? cont’d. P: “You can retake the last exam.” Q: “You can turn this lab in late.” There are four possibilities. 1. P true and Q true , then P Λ Q is true . 2. P true and Q false , then P Λ Q is false . 3. P false and Q true , then P Λ Q is false . 4. P false and Q false , then P Λ Q is false .

7. Truth Table for Conjunction T T F F T F T F T F F F P Λ Q P Q Case 1 Case 2 Case 3 Case 4

8. 3.2 Question 1 What is the truth value of the statement, “Caracas is in Venezuela AND Bogota is in Italy”? 1. True 2. False

9. When is Disjunction True? Suppose I tell the class that for this unit you will receive full credit if “ You do the homework quiz or you do the lab .” Let P be the statement “ You do the homework quiz ,” and let Q be the statement “ You do the lab .” In this case a “truth” is equal to receiving full credit

10. When is Disjunction True? cont’d. P: “You do the homework quiz.” Q: “You do the lab.” There are four possibilities: 1. P true and Q true , then P V Q is true . 2. P true and Q false , then P V Q is true . 3. P false and Q true , then P V Q is true . 4. P false and Q false , then P V Q is false .

11. Truth Table for Disjunction T T F F T F T F T T T F P V Q P Q Case 1 Case 2 Case 3 Case 4

12. 3.2 Question 2 What is the truth value of the statement, “Caracas is in Venezuela or Bogota is in Italy”? 1. True 2. False

13. Truth Table Summary You can remember the truth tables for ~ (not) , Λ (and) , and, V (or) by remembering the following: ~(not) - Truth value is always the opposite Λ (and) - Always false, except when both are true V (or) - Always true, except when both are false

14. Making a Truth Table Example Let’s look at making truth tables for a statement involving only ONE Λ or V of simple statements P and Q and possibly negated simple statements ~P and ~Q. For example, let’s make a truth table for the statement ~P V Q

15. Truth Table for ~P V Q T T F F T F T F P ~P Q Q Opposite of Column 1 F F T T Same as Column 2 T F T F T F T T Final Answer column V

16. Another Example: P Λ ~Q T T F F T F T F P P Q ~Q Same as Column 1 T T F F Opposite of Column 2 F T F T F T F F Final Answer column Λ

17. 3.2 Question 3 What is the answer column in the truth table of the statement ~P Λ ~Q ? 1. T 2. T 3. F F F F F T F F F T

18. ~P Λ ~Q Stop Day 1 T T F F T F T F P ~P Q ~Q Opposite of Column 1 F F T T Opposite of Column 2 F T F T F F F T Final Answer column Λ

19. More Complicated Truth Tables Now suppose we want to make a truth table for a more complicated statement, (P V ~Q) V (~P Λ Q) We set the truth table up as before. Our final answer will go under the most dominant connective not in parentheses ( the one in the middle )

20. More Complicated Truth Tables Final Answer T T F F Opposite of Column 1 Opposite of Column 2 Same as Column 2 Same as Column 1 F T F T OR T T F T F F T T T F T F AND F F T F T T T T

21. More Complicated Truth Tables Now let’s make a truth table for (P V ~Q) Λ (~P Λ Q) Each of the statements in parentheses ( P V ~Q) and (~P Λ Q) are just like the statements we did previously, so we fill in their truth tables as we just did.

22. More Complicated Truth Tables Final Answer T T F F Opposite of Column 1 Opposite of Column 2 Same as Column 2 Same as Column 1 F T F T OR T T F T F F T T T F T F AND F F T F F F F F P Q ( P ~Q ) ( ~P Q ) T T T F F T F F

23. Constructing Truth Tables with Three Simple Statements So far all the compound statements we have considered have contained only two simple statements (P and Q), with only four true-false possibilities. P Q Case 1 T T Case 2 T F Case 3 F T Case 4 F F

24. Constructing Truth Tables with Three Simple Statements cont’d. When a compound statement consists of three simple statements (P, Q, and R), there are now eight possible true-false combinations.

25. Constructing Truth Tables with Three Simple Statements cont’d. P Q R Case 1 T T T Case 2 T T F Case 3 T F T Case 4 T F F Case 5 F T T Case 6 F T F Case 7 F F T Case 8 F F F

26. A Three Statement Example Lets construct a truth table for the statement (P V Q) Λ ~R using the same techniques as before. Remember, there are not more possible combinations because we added a third statement

27. A Three Statement Example T T T T F F F F T T F F T T F F F T F T F T F T T T T T T T F F F T F T F T F F P Q R (P Q) ~R T T T T T F T F T T F F F T T F T F F F T F F F Final Answer

28. Practice Determine the Truth Value for the statement IF: P is true, Q is false, and R is true (~ P V ~ Q) Λ ( ~R V ~ P)

29. Practice Translate into symbols. Then construct a truth table and indicate under what conditions the compound statement is TRUE. Tanisha owns a convertible and Joan does not own a Volvo.

30. Practice Construct a Truth Table for the following compound statement: R V(P Λ ~ Q)

31. DeMorgans Law (this guy again?)

32. More Complicated Truths; Quantifiers Quantifiers- Give an Amount to a statement Examples; All No/None Some Half At least one This makes a Negation (~) more difficult to define Find the Negation of; Some Do All do None do At least one

33. Negations of Quantifiers Some do All do None do At least one does None do (All do not) Some do Not (Not all do) Some do (None do not) None do

34. Examples of Negations with quantifiers Some girls play soccer All boys are immature No students read books At least one person likes anchovies No Girls play soccer Not all boys are immature (some are not immature) Some students read books No one likes anchovies