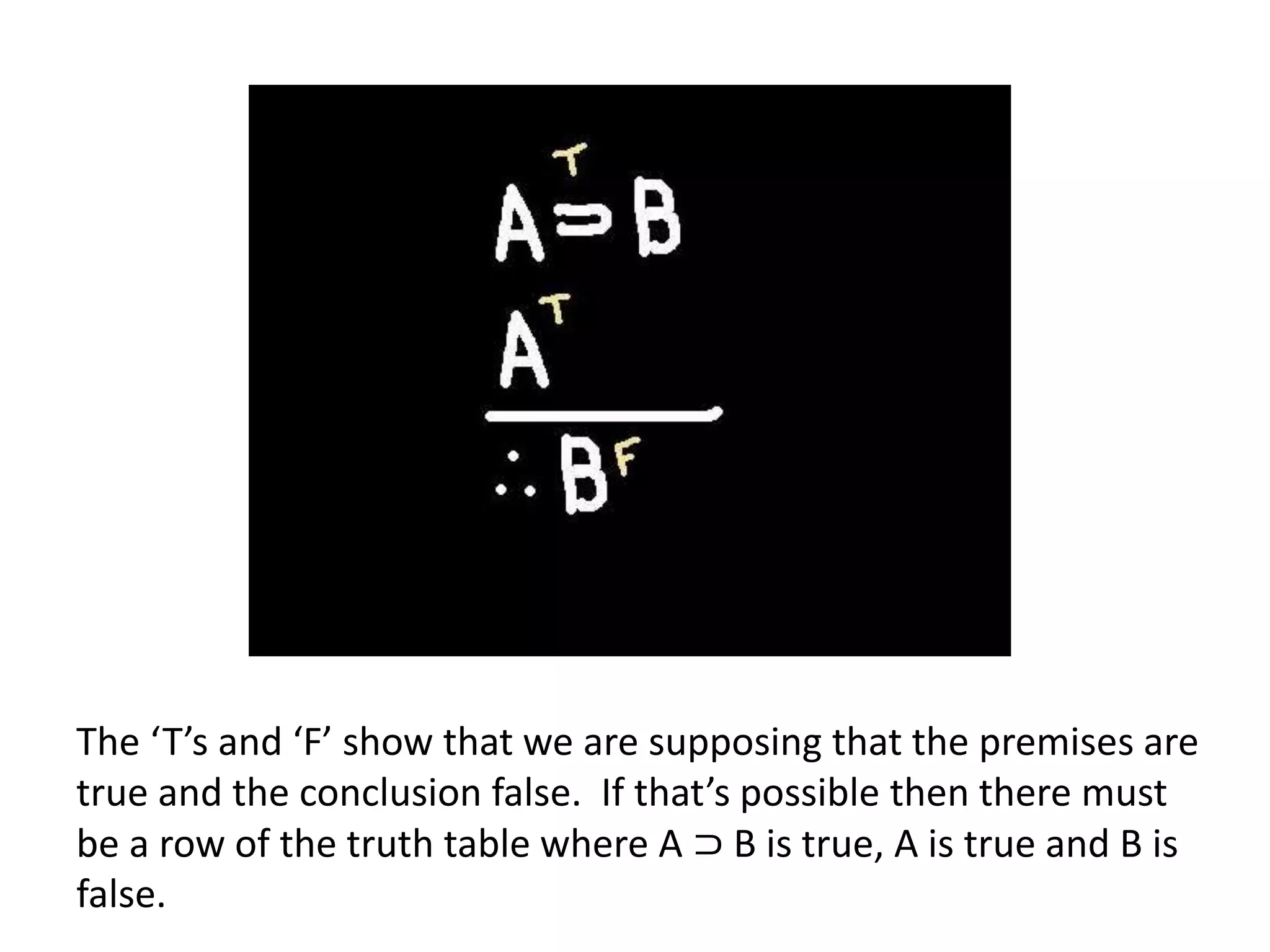
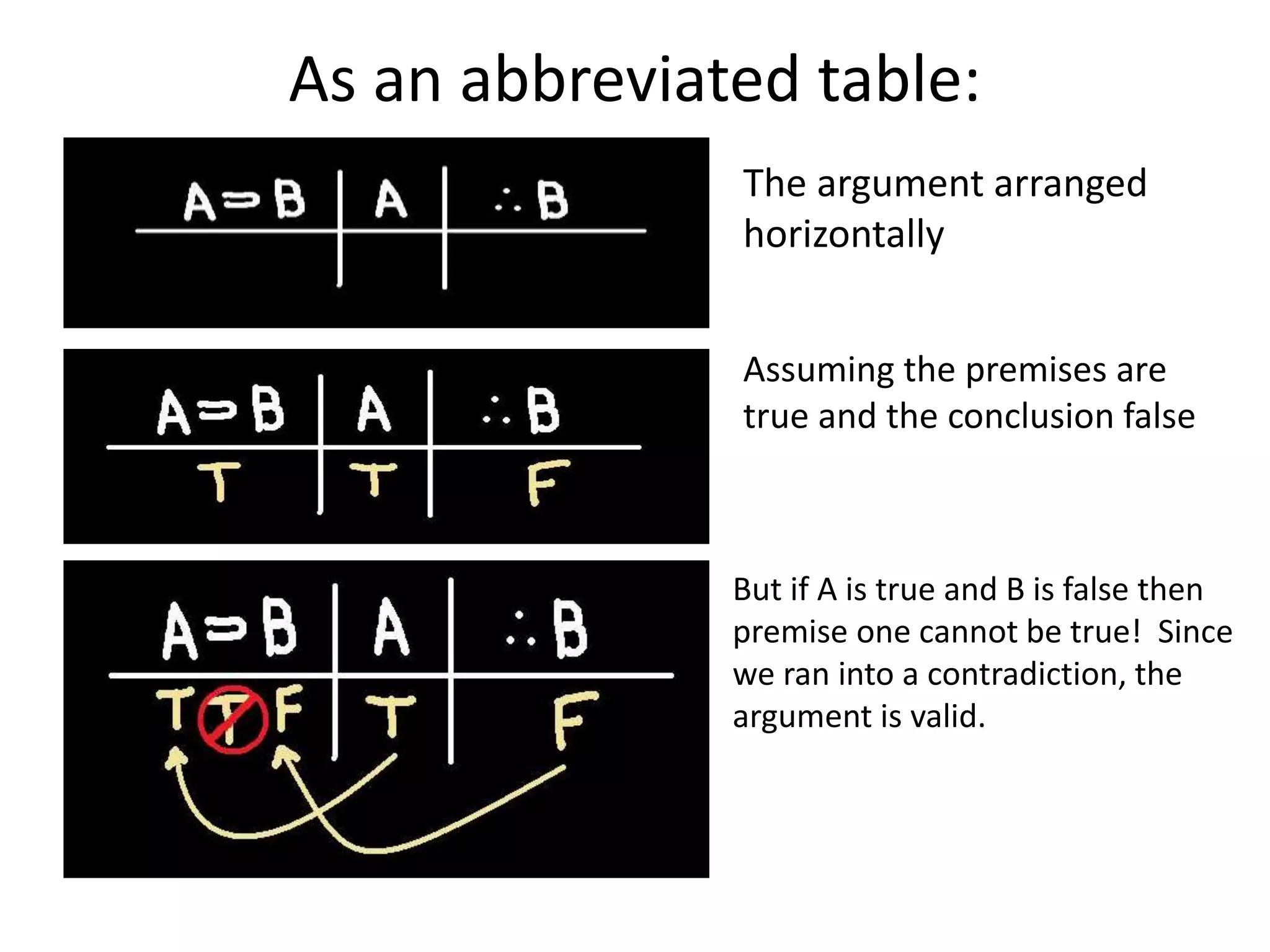
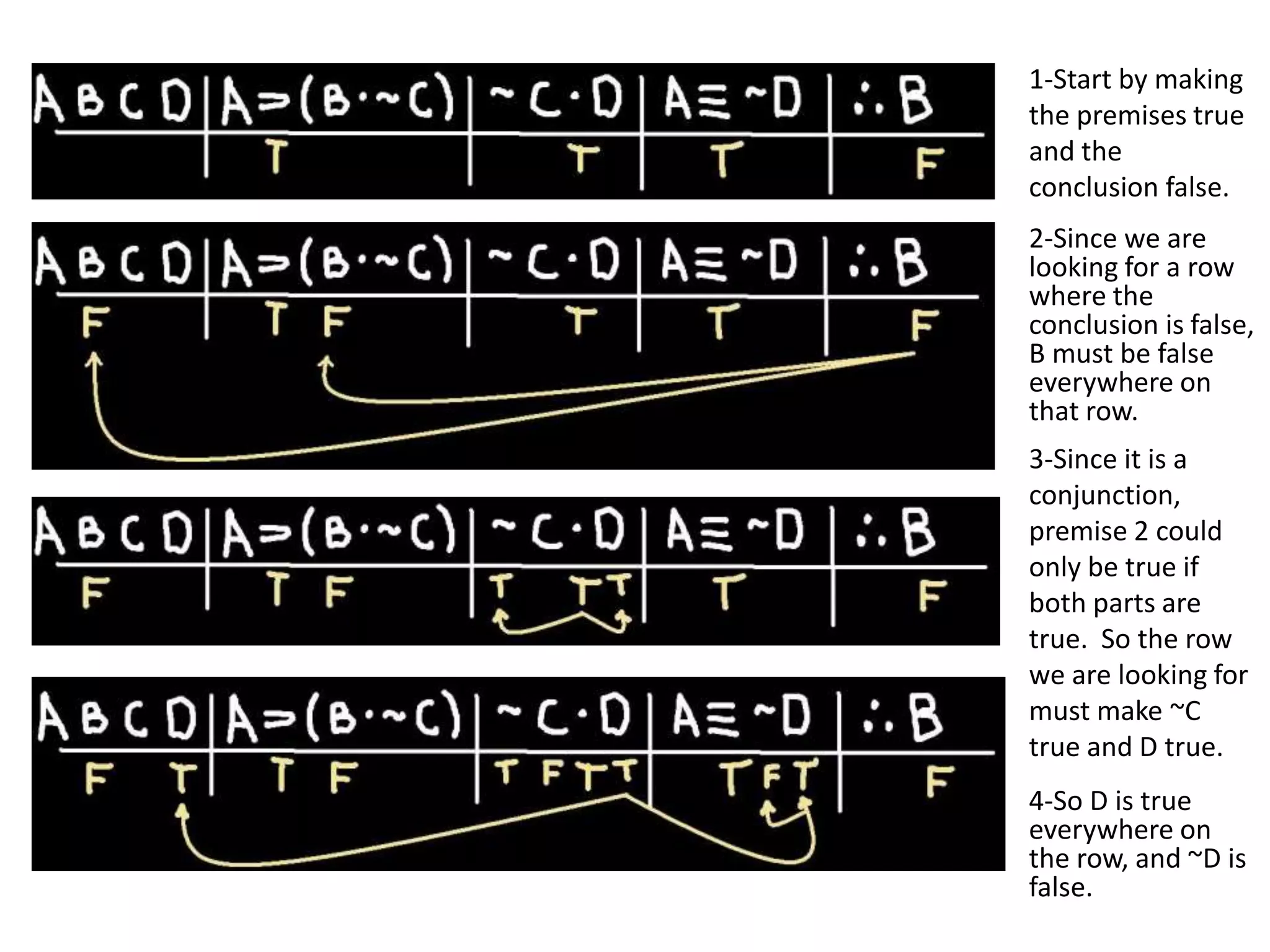
- Abbreviated truth tables check an argument's validity by assuming the premises are true and conclusion is false, working backwards to assign true/false values to statements. - For the argument "If A then B, A. Therefore B", assuming A is true and B is false leads to a contradiction, showing the argument is valid. - More complex arguments may involve choices when multiple assignments could satisfy premises/conclusion. Finding a contradiction means that choice leads to a valid argument; an assignment without contradiction means the argument is invalid.

1. Abbreviated Truth Tables
D. Yeakel

2. The Concept
When using abbreviated tables to check an argument
for validity we are looking for the same thing we
were looking for with regular tables: a row with all
true premises and a false conclusion. However the
approach is reversed.
Instead of starting with assignments of true and false
to component letters, with abbreviated tables we
begin by assuming that the premises are true and
the conclusion is false. Then we work backwards
to an assignment of true and false to the
component letters (if there is one).
Consider the simple argument form on the next slide:

3. Suppose we wanted to check this argument form (commonly
called ‘Modus Ponens’) for validity. A regular table wouldn’t be
too much effort for this one, but there’s an even shorter method.

4. Modus Ponens
We know that if the argument is invalid then
there is a way to make the premises all true
and the conclusion false.
Let’s suppose that the premises are both true
and the conclusion false. We’ll temporarily
denote that supposition this way:

5. The ‘T’s and ‘F’ show that we are supposing that the premises are
true and the conclusion false. If that’s possible then there must
be a row of the truth table where A ⊃ B is true, A is true and B is
false.

6. But if A is true and B is false then premise one (A⊃B) cannot be
true! It’s a conditional with a true antecedent and false
consequent. Its truth-table definition requires that it be false in
that circumstance.

7. So Modus Ponens is Valid
Now we see that no argument with this form
can be invalid. Any assignment of true and
false to the components (A and B) that makes
the second premise true and the conclusion
false will also make the first premise false. So
there cannot be an assignment that gives it all
true premises and a false conclusion.
The next slide shows the same thing as the last
three pictures, except that now the argument
is presented (almost) in the format we will use
for abbreviated tables.

8. As an abbreviated table:
The argument arranged
horizontally
Assuming the premises are
true and the conclusion false
But if A is true and B is false then
premise one cannot be true! Since
we ran into a contradiction, the
argument is valid.

9. Now, a slightly tougher argument
The argument to the left has
four letters and a regular truth
table would be sixteen rows
long. The abbreviated table will
take much less effort. First,
write the argument as you
would if you were going to do a
full table. Include the sentence
letters on the left side as you
would in a regular table. The
result is below.

10. 1-Start by making
the premises true
and the
conclusion false.
4-So D is true
everywhere on
the row, and ~D is
false.
2-Since we are
looking for a row
where the
conclusion is false,
B must be false
everywhere on
that row.
3-Since it is a
conjunction,
premise 2 could
only be true if
both parts are
true. So the row
we are looking for
must make ~C
true and D true.

11. So A is false everywhere
it appears.
Since ~ C is true, C is
false everywhere.
In premise 1: if B is false
and ~C is true then the
conjunction B∙ ~ C is false.
In premise 3: If the
premise (A≡~D) is true
and the right side (~ D) is
false then the left side (A)
must also be false.
There’s no
contradiction on the
table since a false ⊃
false conditional is
true.
We’ve learned that if we had done a full 16 row table then the FFFT row would have all
true premises and a false conclusion and show the argument to be invalid.

12. Choices
• The idea of abbreviated tables is that if trying to give the argument
true premises and a false conclusion leads to contradiction then the
argument is valid, but success at finding such a row is failure
(invalidity) for the argument.
• The examples so far have been nice at least in that every step of the
abbreviated table was ‘forced.’ For example, there’s only one way to
make A≡D true if D is true (A must be false).
• But what if all we knew was that A≡D was true and we had no
information about A or D? We wouldn’t be forced. We’d have to
make a choice.
• Running into a contradiction after making an unforced choice
doesn’t imply validity. Some other choice might have led to a row
that shows the argument invalid. Finding a row along a choice path
does imply invalidity though, because you only need one row with
true premises and a false conclusion to show an argument invalid.
• Next is an example of an abbreviated table with a choice.

13. Notice that we aren’t forced anywhere. There are three ways to make a
disjunction true, three ways to make a conditional true and two ways to make
a biconditional false. Below, I made a choice in the conclusion since there are
just two possibilities (instead of three). The circled ‘1’ to the right of the table
below shows that A true and B false is the first option for making the
conclusion false.
To the left is the argument in standard form.
Above, the argument is set up for an abbreviated table
with premises set to true and conclusion set to false.

14. 3- We don’t have to think
about C because we already
have a contradiction. Premise
2 can’t be true if it has a true
antecedent and a false
consequent. However,
because we made a choice
earlier, we aren’t finished.
We’ve only showed that the
option we chose for the
conclusion leads to
contradiction, not that every
possible way of making the
premises true and the
conclusion false leads to
contradiction!
1- Since A is true in the
conclusion it must be true
everywhere it appears.
2- Since B is false in the
conclusion it must be false
everywhere it appears.
4-So, we go back to the point
of the choice and try the
other way to make the
conclusion false.

15. 3- Since ~A is true, premise
one is true no matter what
value C has. So we have to
make another choice, but
this one obviously doesn’t
matter. We have a row that
makes the premises true
and the conclusion false.
In fact, we know that a
complete table would have
two rows that show the
argument invalid: the FTT
row and the FTF row.
1- A is false
everywhere on the
row.
2- B is true
everywhere on the
row.