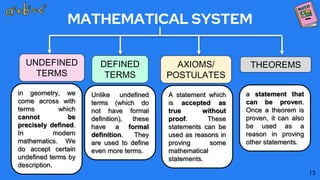
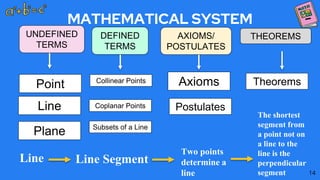
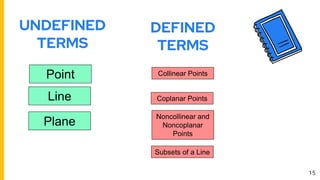
The document discusses the key components of a mathematical system: 1. Undefined terms are concepts that cannot be precisely defined, such as points, lines, and planes in geometry. 2. Defined terms have a formal definition using undefined terms or other defined terms, such as line segments, rays, and collinear/coplanar points. 3. Axioms or postulates are statements assumed to be true without proof, which can be used to prove theorems. 4. Theorems are statements that have been formally proven using axioms, postulates and previously proven theorems. The four components are related such that defined terms are defined using undefined terms, axioms are

1. Mathematical
system

2. Pre-test
2
1. What do you call the statements that are assumed to
be true and do not
need proof?
A. axioms
B. defined terms
C. theorems
D. undefined terms

3. Pre-test
3
2. There are four parts of the Mathematical system.
Which of the following is not a part of the mathematical
system?
A. corollary
B. theorems
C. axioms or postulate
D. defined and undefined terms

4. Pre-test
4
3. Which of the following statements is true about axioms
or postulates?
A. These are concepts that need to be defined.
B. These are statements accepted after it is proved
deductively.
C. These are concepts that can be defined using the
undefined terms.
D. These are statements assumed to be true and need
no further proof.

5. Pre-test
5
4. Which of the following statements is true about a
postulate?
A. It is never accepted to be true.
B. It is accepted as true without a formal proof.
C. It is only accepted as true after being formally proven.
D. It is usually not obvious as true, so it must be proven.

6. Pre-test
6
5. Which of the following best describes a theorem?
A. It is the same thing as a postulate.
B. It is a statement that is accepted as true without a
formal proof.
C. It is a statement that is impossible to be proven by
mathematical reasoning.
D. It is a statement that has been formally proven using
mathematical reasoning.

7. Pre-test
7
6. Which of the following is NOT a property of
Mathematical system?
A. conjecture C. postulates
B. define terms D. theorems

8. Pre-test
8
7. Which of the following statements is true about
defined terms?
A. These are concepts that need to be defined.
B. These are statements accepted after it is proved
deductively.
C. These are concepts that can be defined using the
undefined terms.
D. These are statements assumed to be true and need
no further proof.

9. Pre-test
9
8. Which of the following illustrates reflexive property?
A. (𝐴𝐵 + 𝐵𝐶) + 𝐶𝐷 = (𝐴𝐵 + 𝐵𝐶) + 𝐶𝐷
B. (𝐴𝐵 + 𝐵𝐶) + 𝐶𝐷 = (𝐵𝐶 + 𝐴𝐵) + 𝐶𝐷
C. (𝐴𝐵 + 𝐵𝐶) + 𝐶𝐷 = 𝐴𝐵 + 𝐵𝐶 + 𝐶𝐷
D. (𝐴𝐵 + 𝐵𝐶) + 𝐶𝐷 = 𝐶𝐷 + (𝐴𝐵 + 𝐵𝐶)

10. Pre-test
10
9. Which of the following illustrates distributive property
of equality?
A. 3 + 4 = 4(3) + 3(4)
B.5(2) + 6(7) = 5(7) + 6(2)
C.8(𝑥 + 𝑦 + 𝑧) = 8𝑥 + 8𝑦 + 8𝑧
D.−8(𝑥 + 𝑦 + 𝑧) = −8𝑥 + 𝑧 + 𝑦

11. Pre-test
11
10. Which of the following is a commutative axiom?
A. 2 + 3 = 2 + 3 C. 2 ∙ 3 = 2 ∙ 3
B. 2 + 3 = 3 + 2 D. (2 + 3) = 2(3) + 3(2)

12. Objectives:
12
1.Define each part of the mathematical system;
a. Undefined terms
b. Defined terms
c. Postulates
d. Theorems;
2. Illustrate how the four parts of mathematical
system related to one another.

13. MATHEMATICAL SYSTEM
13
UNDEFINED
TERMS
DEFINED
TERMS
AXIOMS/
POSTULATES
THEOREMS
in geometry, we
come across with
terms which
cannot be
precisely defined.
In modern
mathematics. We
do accept certain
undefined terms by
description.
Unlike undefined
terms (which do
not have formal
definition), these
have a formal
definition. They
are used to define
even more terms.
A statement which
is accepted as
true without
proof. These
statements can be
used as reasons in
proving some
mathematical
statements.
a statement that
can be proven.
Once a theorem is
proven, it can also
be used as a
reason in proving
other statements.

14. MATHEMATICAL SYSTEM
14
UNDEFINED
TERMS
DEFINED
TERMS
AXIOMS/
POSTULATES
THEOREMS
Point
Line
Plane
Collinear Points
Coplanar Points
Subsets of a Line
Axioms
Postulates
Theorems
Line Line Segment
Two points
determine a
line
The shortest
segment from
a point not on
a line to the
line is the
perpendicular
segment

15. UNDEFINED
TERMS
15
Point
Line
Plane
DEFINED
TERMS
Collinear Points
Coplanar Points
Subsets of a Line
Noncollinear and
Noncoplanar
Points

16. 16

17. 17

18. 18

19. 19

20. Directions: Identify whether each of the following
represents a point, line or a plane.
1. Stars in the sky
2. Curtain rod
3. Edge of a ruler
4. Cartolina
5. A knot on a piece of thread
6. A clothesline
20
7. Top of a box
8. Page of a book
9. A magic wand
10. Button
11. Mole
12. Handkerchief
Point
Line
Line
Plane
Point
Line
Plane
Plane
Line
Point
Point
Plane

21. Point
21

22. Point
22
• A point is a position in space. It has only location but no
dimension; length, width, thickness and does not occupy
an area.
• It is named using a CAPITAL LETTER and it can be
modeled by a dot.
A
B
C
D
• All other geometric figures are made up of a collection of
points.

23. Line
23
• A straight, continuous arrangement of infinitely many
points. Its length is infinite. It extends infinitely in two
directions. And it has no thickness.
• The arrowhead symbolizes infinity
• Lines are named by a single lower case script letter or by
any two points on a line

24. 24
Line
d
line d d
A B line AB line BA
AB BA
Two points determine a line

25. Plane
● A flat surface that extends along its length and
width. It is like an “infinite sheet of paper”.
● It has length and width but no thickness
● It is named by a single script CAPITAL LETTER or by
any three points in the plane which are not on the
same line.
25

26. Plane
● A flat surface that extends along its length and
width. It is like an “infinite sheet of paper”.
● It has length and width but no thickness
● It is named by a single script CAPITAL LETTER or by
any three points in the plane which are not on the
same line.
26
D
plane D
L I
E F
plane LIF
plane IFE
plane LEF
plane EFI
plane LIFE
● At least three noncollinear
points determine a plane.

27. Defined Terms
27
Collinear Points Non-collinear Points
A B C
Points A, B, and C are colinear
points
A B
C
Points A, B, and C are non-
colinear points
are points that lie on the same line are points that do not lie on the
same line

28. 28
Defined Terms
Coplanar Points Non-coplanar Points
A
B
C
Points A, B, and C are coplanar
points
B
C
A
Points A, B, and C are non-
coplanar points
are points that lie in the same
plane
are points that do not lie in the
same plane

29. Subsets of a Line
LINE SEGMENT
29
A B
A B A B B
A C
A line segment is a part of a
line consisting two
endpoints and all the points
in between.
A line segment may be called:
AB or BA
Its endpoints are A and B.
RAY
A ray is a part of a line with
one endpoint and extending
in only one direction.
A ray is named with its endpoint
first, followed by another point
on the ray.
The ray can be named AB read
as “ray AB”
OPPOSITE RAY
are rays with a common
endpoint but extending in
opposite directions.
Common Endpoint: B
Opposite rays:
BA and BC
B is between points A and C

30. 30
Let’s Try!
1. Name all the points.
A, W, X, Y and Z
2. Name all the lines using a script letter.
line a line b line c line d
3. What is the other name for line a?
line WZ or line ZW
4. Using a script letter, name a plane form
by the four lines.
plane L
5. Name the plane in three different ways
using three points.
plane WXY plane XYZ plane WZY
W X
Z Y
L
A
c
d
a b

31. 31

32. 32
Assignment