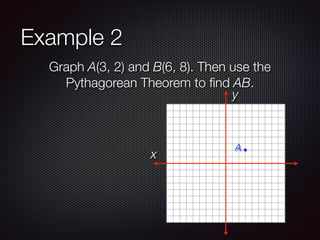
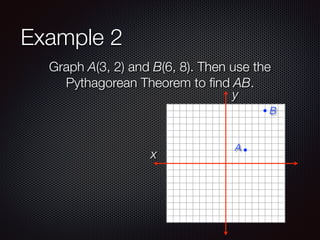
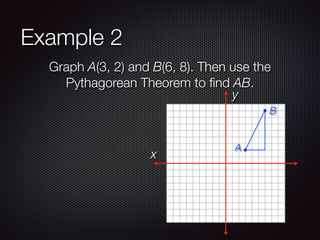
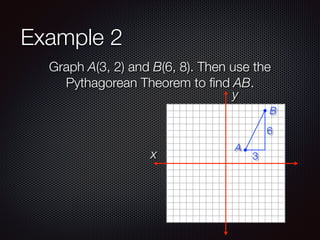
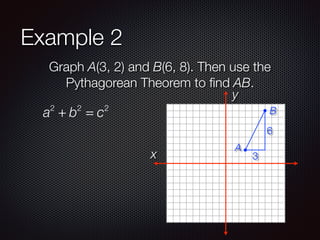
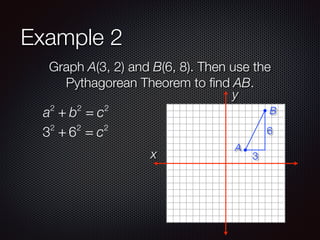
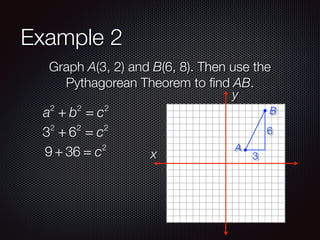
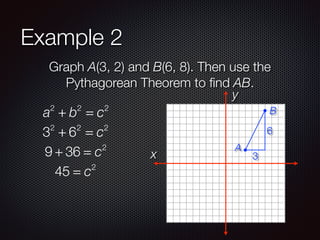
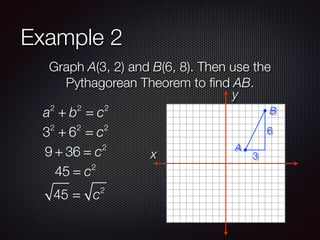
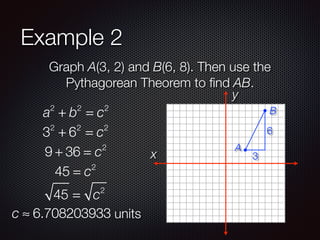
This document discusses distance and midpoints between points in a coordinate plane. It defines distance as the length of a segment between two points and the Pythagorean theorem. The midpoint of a segment is the point halfway between the two endpoints. Examples are provided to demonstrate calculating distance and midpoints using formulas like the distance formula and midpoint formula.

1. Section 1-3
Distance and Midpoints

2. Essential Questions
How do you find the distance between two points?
How do you find the midpoint of a segment?

3. Vocabulary
1. Pythagorean Theorem:
2. Distance:

4. Vocabulary
1. Pythagorean Theorem: a2
+ b2
= c2
, where a and
b are legs of a right triangle, and c is the
hypotenuse
2. Distance:

5. Vocabulary
1. Pythagorean Theorem: a2
+ b2
= c2
, where a and
b are legs of a right triangle, and c is the
hypotenuse
2. Distance: The length of the segment formed
between two points

6. Vocabulary
1. Pythagorean Theorem: a2
+ b2
= c2
, where a and
b are legs of a right triangle, and c is the
hypotenuse
2. Distance: The length of the segment formed
between two points
d = (x2
− x1
)2
+ (y2
− y1
)2
for (x1
, y1
) and (x2
, y2
)

7. Vocabulary
3. Midpoint:
4. Segment Bisector:

8. Vocabulary
3. Midpoint: The point on a segment that is halfway
between the endpoints
4. Segment Bisector:

9. Vocabulary
3. Midpoint: The point on a segment that is halfway
between the endpoints
M =
x1
+ x2
2
,
y1
+ y2
2
⎛
⎝
⎜
⎞
⎠
⎟ for (x1
, y1
) and (x2
, y2
)
4. Segment Bisector:

10. Vocabulary
3. Midpoint: The point on a segment that is halfway
between the endpoints
M =
x1
+ x2
2
,
y1
+ y2
2
⎛
⎝
⎜
⎞
⎠
⎟ for (x1
, y1
) and (x2
, y2
)
4. Segment Bisector: Any segment, line, or plane
that intersects another segment at its midpoint

11. Example 1
Use the number line to find DJ.
−4 −3 −2 −1 0 1 2 3 4
J D

12. Example 1
Use the number line to find DJ.
−4 −3 −2 −1 0 1 2 3 4
J D
x2
− x1

13. Example 1
Use the number line to find DJ.
−4 −3 −2 −1 0 1 2 3 4
J D
x2
− x1
4 − (−4)

14. Example 1
Use the number line to find DJ.
−4 −3 −2 −1 0 1 2 3 4
J D
x2
− x1
4 − (−4) 4 + 4

15. Example 1
Use the number line to find DJ.
−4 −3 −2 −1 0 1 2 3 4
J D
x2
− x1
4 − (−4) 4 + 4 8

16. Example 1
Use the number line to find DJ.
−4 −3 −2 −1 0 1 2 3 4
J D
x2
− x1
4 − (−4) 4 + 4 8 8

17. Example 1
Use the number line to find DJ.
−4 −3 −2 −1 0 1 2 3 4
J D
x2
− x1
4 − (−4) 4 + 4 8 8
8 units

18. Example 2
Graph A(3, 2) and B(6, 8). Then use the
Pythagorean Theorem to find AB.

19. Example 2
Graph A(3, 2) and B(6, 8). Then use the
Pythagorean Theorem to find AB.
x
y

20. Example 2
Graph A(3, 2) and B(6, 8). Then use the
Pythagorean Theorem to find AB.
x
y
A

21. Example 2
Graph A(3, 2) and B(6, 8). Then use the
Pythagorean Theorem to find AB.
x
y
A
B

22. Example 2
Graph A(3, 2) and B(6, 8). Then use the
Pythagorean Theorem to find AB.
x
y
A
B

23. Example 2
Graph A(3, 2) and B(6, 8). Then use the
Pythagorean Theorem to find AB.
x
y
A
B
3
6

24. Example 2
Graph A(3, 2) and B(6, 8). Then use the
Pythagorean Theorem to find AB.
x
y
A
B
3
6
a2
+ b2
= c2

25. Example 2
Graph A(3, 2) and B(6, 8). Then use the
Pythagorean Theorem to find AB.
x
y
A
B
3
6
a2
+ b2
= c2
32
+ 62
= c2

26. Example 2
Graph A(3, 2) and B(6, 8). Then use the
Pythagorean Theorem to find AB.
x
y
A
B
3
6
a2
+ b2
= c2
32
+ 62
= c2
9 + 36 = c2

27. Example 2
Graph A(3, 2) and B(6, 8). Then use the
Pythagorean Theorem to find AB.
x
y
A
B
3
6
a2
+ b2
= c2
32
+ 62
= c2
9 + 36 = c2
45 = c2

28. Example 2
Graph A(3, 2) and B(6, 8). Then use the
Pythagorean Theorem to find AB.
x
y
A
B
3
6
a2
+ b2
= c2
32
+ 62
= c2
9 + 36 = c2
45 = c2
45 = c2

29. Example 2
Graph A(3, 2) and B(6, 8). Then use the
Pythagorean Theorem to find AB.
x
y
A
B
3
6
a2
+ b2
= c2
32
+ 62
= c2
9 + 36 = c2
45 = c2
45 = c2
c ≈ 6.708203933 units

30. Example 3
Use the distance formula to find the distance
between A(3, 2) and B(6, 8).

31. Example 3
Use the distance formula to find the distance
between A(3, 2) and B(6, 8).
d = (x2
− x1
)2
+ (y2
− y1
)2

32. Example 3
Use the distance formula to find the distance
between A(3, 2) and B(6, 8).
d = (x2
− x1
)2
+ (y2
− y1
)2
= (6 − 3)2
+ (8 − 2)2

33. Example 3
Use the distance formula to find the distance
between A(3, 2) and B(6, 8).
d = (x2
− x1
)2
+ (y2
− y1
)2
= (6 − 3)2
+ (8 − 2)2
= 32
+ 62

34. Example 3
Use the distance formula to find the distance
between A(3, 2) and B(6, 8).
d = (x2
− x1
)2
+ (y2
− y1
)2
= (6 − 3)2
+ (8 − 2)2
= 32
+ 62
= 9 + 36

35. Example 3
Use the distance formula to find the distance
between A(3, 2) and B(6, 8).
d = (x2
− x1
)2
+ (y2
− y1
)2
= (6 − 3)2
+ (8 − 2)2
= 32
+ 62
= 9 + 36
= 45

36. Example 3
Use the distance formula to find the distance
between A(3, 2) and B(6, 8).
d = (x2
− x1
)2
+ (y2
− y1
)2
= (6 − 3)2
+ (8 − 2)2
= 32
+ 62
= 9 + 36
= 45
≈ 6.708203933 units

37. Example 4
Find the midpoint of AB for points A(3, 2) and
B(6, 8).

38. Example 4
Find the midpoint of AB for points A(3, 2) and
B(6, 8).
M =
x1
+ x2
2
,
y1
+ y2
2
⎛
⎝
⎜
⎞
⎠
⎟

39. Example 4
Find the midpoint of AB for points A(3, 2) and
B(6, 8).
M =
x1
+ x2
2
,
y1
+ y2
2
⎛
⎝
⎜
⎞
⎠
⎟ =
3 + 6
2
,
2 + 8
2
⎛
⎝
⎜
⎞
⎠
⎟

40. Example 4
Find the midpoint of AB for points A(3, 2) and
B(6, 8).
M =
x1
+ x2
2
,
y1
+ y2
2
⎛
⎝
⎜
⎞
⎠
⎟ =
3 + 6
2
,
2 + 8
2
⎛
⎝
⎜
⎞
⎠
⎟
=
9
2
,
10
2
⎛
⎝
⎜
⎞
⎠
⎟

41. Example 4
Find the midpoint of AB for points A(3, 2) and
B(6, 8).
M =
x1
+ x2
2
,
y1
+ y2
2
⎛
⎝
⎜
⎞
⎠
⎟ =
3 + 6
2
,
2 + 8
2
⎛
⎝
⎜
⎞
⎠
⎟
=
9
2
,
10
2
⎛
⎝
⎜
⎞
⎠
⎟ =
9
2
,5
⎛
⎝
⎜
⎞
⎠
⎟

42. Example 4
Find the midpoint of AB for points A(3, 2) and
B(6, 8).
M =
x1
+ x2
2
,
y1
+ y2
2
⎛
⎝
⎜
⎞
⎠
⎟ =
3 + 6
2
,
2 + 8
2
⎛
⎝
⎜
⎞
⎠
⎟
=
9
2
,
10
2
⎛
⎝
⎜
⎞
⎠
⎟ =
9
2
,5
⎛
⎝
⎜
⎞
⎠
⎟ or 4.5,5( )

43. Example 5
Find the coordinates of U if F(−2, 3) is the
midpoint of UO and O has coordinates of (8, 6).

44. Example 5
Find the coordinates of U if F(−2, 3) is the
midpoint of UO and O has coordinates of (8, 6).
M =
x1
+ x2
2
,
y1
+ y2
2
⎛
⎝
⎜
⎞
⎠
⎟

45. Example 5
Find the coordinates of U if F(−2, 3) is the
midpoint of UO and O has coordinates of (8, 6).
M =
x1
+ x2
2
,
y1
+ y2
2
⎛
⎝
⎜
⎞
⎠
⎟ (−2,3) =
x + 8
2
,
y + 6
2
⎛
⎝
⎜
⎞
⎠
⎟

46. Example 5
Find the coordinates of U if F(−2, 3) is the
midpoint of UO and O has coordinates of (8, 6).
M =
x1
+ x2
2
,
y1
+ y2
2
⎛
⎝
⎜
⎞
⎠
⎟ (−2,3) =
x + 8
2
,
y + 6
2
⎛
⎝
⎜
⎞
⎠
⎟
−2 =
x + 8
2

47. Example 5
Find the coordinates of U if F(−2, 3) is the
midpoint of UO and O has coordinates of (8, 6).
M =
x1
+ x2
2
,
y1
+ y2
2
⎛
⎝
⎜
⎞
⎠
⎟ (−2,3) =
x + 8
2
,
y + 6
2
⎛
⎝
⎜
⎞
⎠
⎟
−2 =
x + 8
2
i2

48. Example 5
Find the coordinates of U if F(−2, 3) is the
midpoint of UO and O has coordinates of (8, 6).
M =
x1
+ x2
2
,
y1
+ y2
2
⎛
⎝
⎜
⎞
⎠
⎟ (−2,3) =
x + 8
2
,
y + 6
2
⎛
⎝
⎜
⎞
⎠
⎟
−2 =
x + 8
2
i2(2)i( )

49. Example 5
Find the coordinates of U if F(−2, 3) is the
midpoint of UO and O has coordinates of (8, 6).
M =
x1
+ x2
2
,
y1
+ y2
2
⎛
⎝
⎜
⎞
⎠
⎟ (−2,3) =
x + 8
2
,
y + 6
2
⎛
⎝
⎜
⎞
⎠
⎟
−2 =
x + 8
2
i2(2)i( )
−4 = x + 8

50. Example 5
Find the coordinates of U if F(−2, 3) is the
midpoint of UO and O has coordinates of (8, 6).
M =
x1
+ x2
2
,
y1
+ y2
2
⎛
⎝
⎜
⎞
⎠
⎟ (−2,3) =
x + 8
2
,
y + 6
2
⎛
⎝
⎜
⎞
⎠
⎟
−2 =
x + 8
2
i2(2)i( )
−4 = x + 8
x = −12

51. Example 5
Find the coordinates of U if F(−2, 3) is the
midpoint of UO and O has coordinates of (8, 6).
M =
x1
+ x2
2
,
y1
+ y2
2
⎛
⎝
⎜
⎞
⎠
⎟ (−2,3) =
x + 8
2
,
y + 6
2
⎛
⎝
⎜
⎞
⎠
⎟
−2 =
x + 8
2
i2(2)i( )
−4 = x + 8
x = −12
3 =
y + 6
2

52. Example 5
Find the coordinates of U if F(−2, 3) is the
midpoint of UO and O has coordinates of (8, 6).
M =
x1
+ x2
2
,
y1
+ y2
2
⎛
⎝
⎜
⎞
⎠
⎟ (−2,3) =
x + 8
2
,
y + 6
2
⎛
⎝
⎜
⎞
⎠
⎟
−2 =
x + 8
2
i2(2)i( )
−4 = x + 8
x = −12
3 =
y + 6
2
i2

53. Example 5
Find the coordinates of U if F(−2, 3) is the
midpoint of UO and O has coordinates of (8, 6).
M =
x1
+ x2
2
,
y1
+ y2
2
⎛
⎝
⎜
⎞
⎠
⎟ (−2,3) =
x + 8
2
,
y + 6
2
⎛
⎝
⎜
⎞
⎠
⎟
−2 =
x + 8
2
i2(2)i( )
−4 = x + 8
x = −12
3 =
y + 6
2
i22i

54. Example 5
Find the coordinates of U if F(−2, 3) is the
midpoint of UO and O has coordinates of (8, 6).
M =
x1
+ x2
2
,
y1
+ y2
2
⎛
⎝
⎜
⎞
⎠
⎟ (−2,3) =
x + 8
2
,
y + 6
2
⎛
⎝
⎜
⎞
⎠
⎟
−2 =
x + 8
2
i2(2)i( )
−4 = x + 8
x = −12
3 =
y + 6
2
i22i
6 = y + 6

55. Example 5
Find the coordinates of U if F(−2, 3) is the
midpoint of UO and O has coordinates of (8, 6).
M =
x1
+ x2
2
,
y1
+ y2
2
⎛
⎝
⎜
⎞
⎠
⎟ (−2,3) =
x + 8
2
,
y + 6
2
⎛
⎝
⎜
⎞
⎠
⎟
−2 =
x + 8
2
i2(2)i( )
−4 = x + 8
x = −12
3 =
y + 6
2
i22i
6 = y + 6
y = 0

56. Example 5
Find the coordinates of U if F(−2, 3) is the
midpoint of UO and O has coordinates of (8, 6).
M =
x1
+ x2
2
,
y1
+ y2
2
⎛
⎝
⎜
⎞
⎠
⎟ (−2,3) =
x + 8
2
,
y + 6
2
⎛
⎝
⎜
⎞
⎠
⎟
−2 =
x + 8
2
i2(2)i( )
−4 = x + 8
x = −12
3 =
y + 6
2
i22i
6 = y + 6
y = 0
U(−12,0)

57. Example 6
Find PQ if Q is the midpoint of PR.
2x + 3 4x − 1
P Q R

58. Example 6
Find PQ if Q is the midpoint of PR.
2x + 3 4x − 1
P Q R
2x + 3 = 4x − 1

59. Example 6
Find PQ if Q is the midpoint of PR.
2x + 3 4x − 1
P Q R
2x + 3 = 4x − 1
4 = 2x

60. Example 6
Find PQ if Q is the midpoint of PR.
2x + 3 4x − 1
P Q R
2x + 3 = 4x − 1
4 = 2x
x = 2

61. Example 6
Find PQ if Q is the midpoint of PR.
2x + 3 4x − 1
P Q R
2x + 3 = 4x − 1
4 = 2x
x = 2
PQ = 2x + 3

62. Example 6
Find PQ if Q is the midpoint of PR.
2x + 3 4x − 1
P Q R
2x + 3 = 4x − 1
4 = 2x
x = 2
PQ = 2x + 3
PQ = 2(2) + 3

63. Example 6
Find PQ if Q is the midpoint of PR.
2x + 3 4x − 1
P Q R
2x + 3 = 4x − 1
4 = 2x
x = 2
PQ = 2x + 3
PQ = 2(2) + 3
PQ = 4 + 3

64. Example 6
Find PQ if Q is the midpoint of PR.
2x + 3 4x − 1
P Q R
2x + 3 = 4x − 1
4 = 2x
x = 2
PQ = 2x + 3
PQ = 2(2) + 3
PQ = 4 + 3
PQ = 7 units

65. Problem Set

66. Problem Set
p. 30 #1-11, 19-31, 47, 49, 53 (odds only)
“Learn from yesterday, live for today, hope for
tomorrow. The important thing is not to stop
questioning.” - Albert Einstein