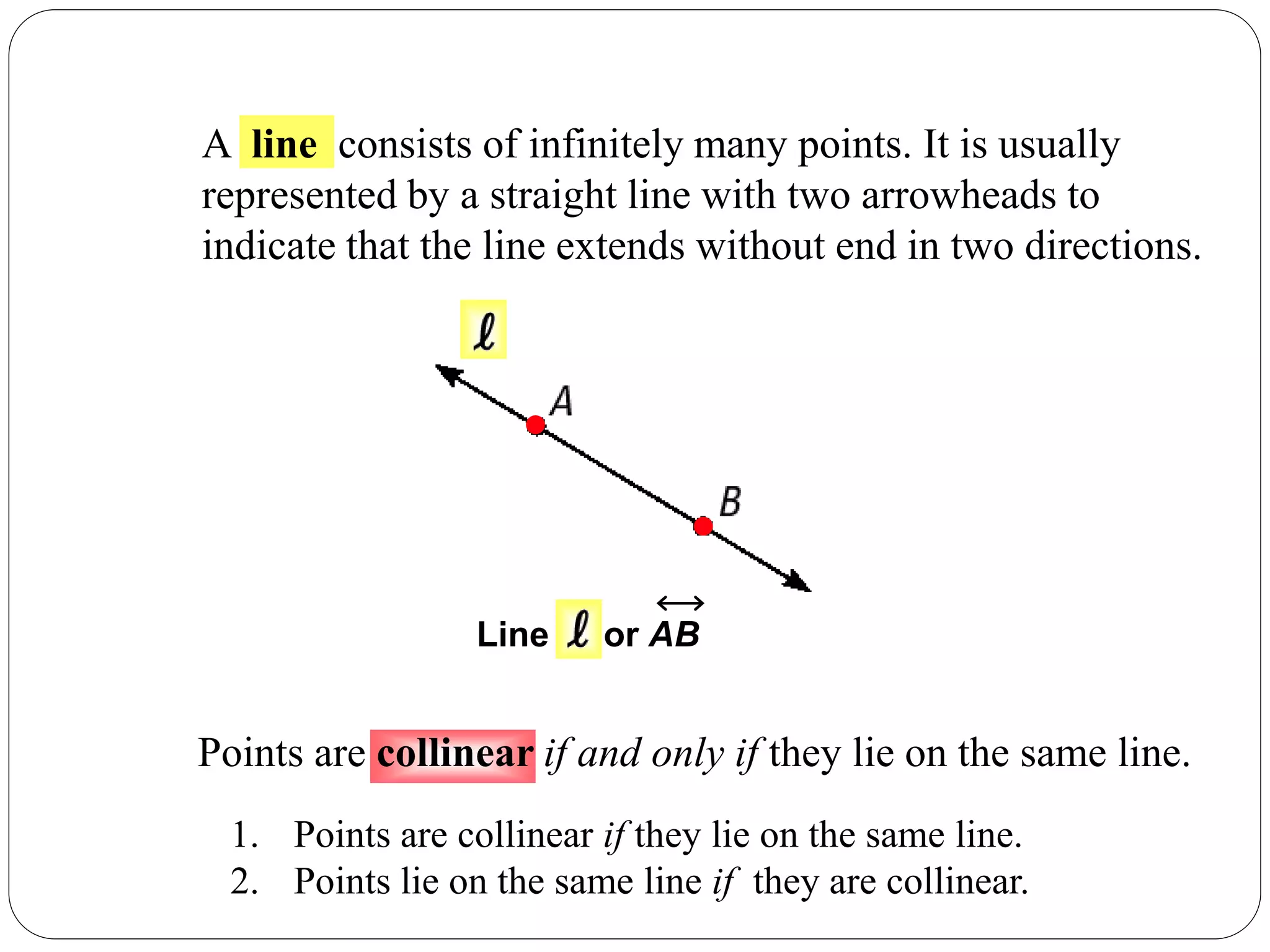
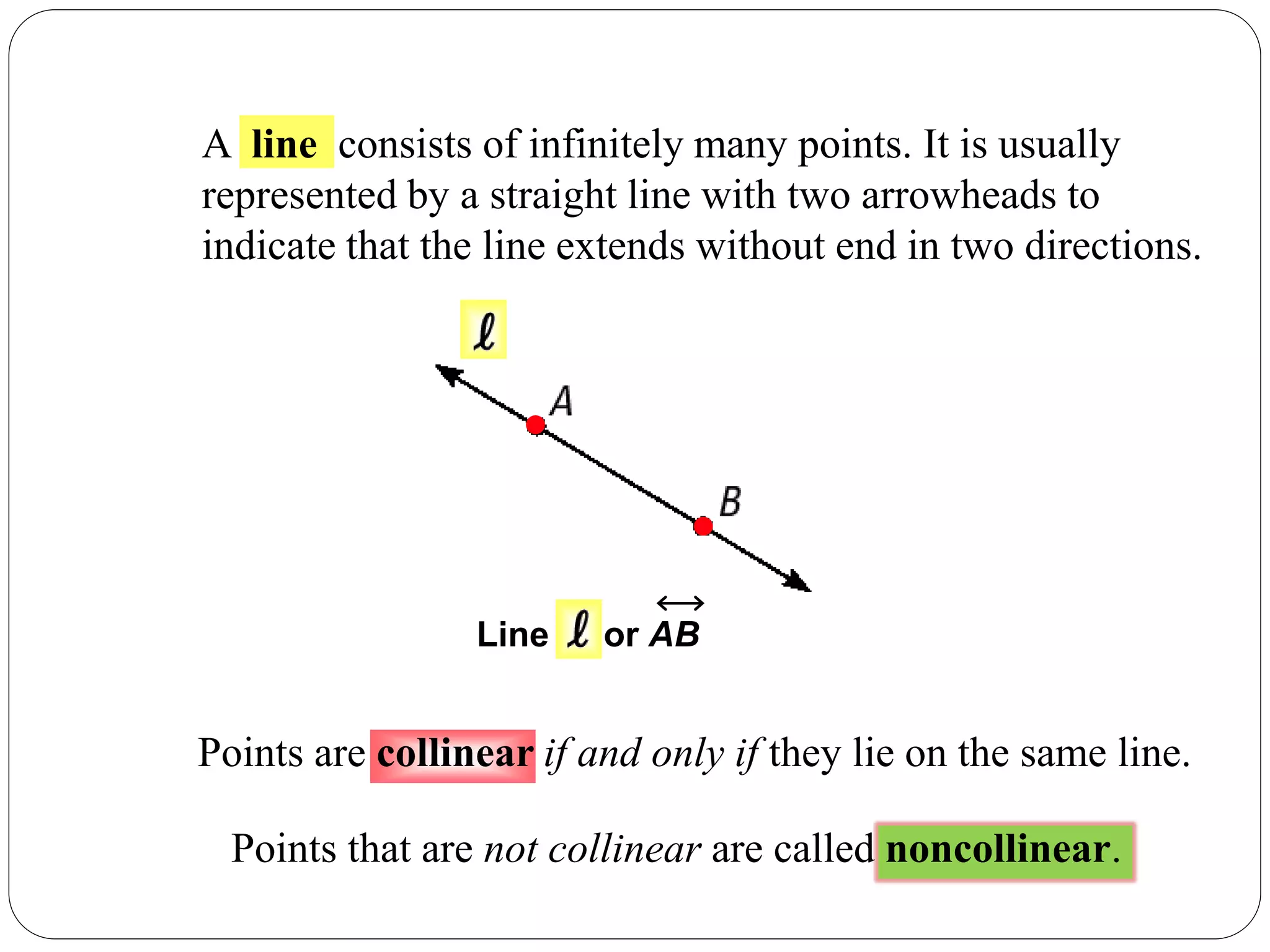
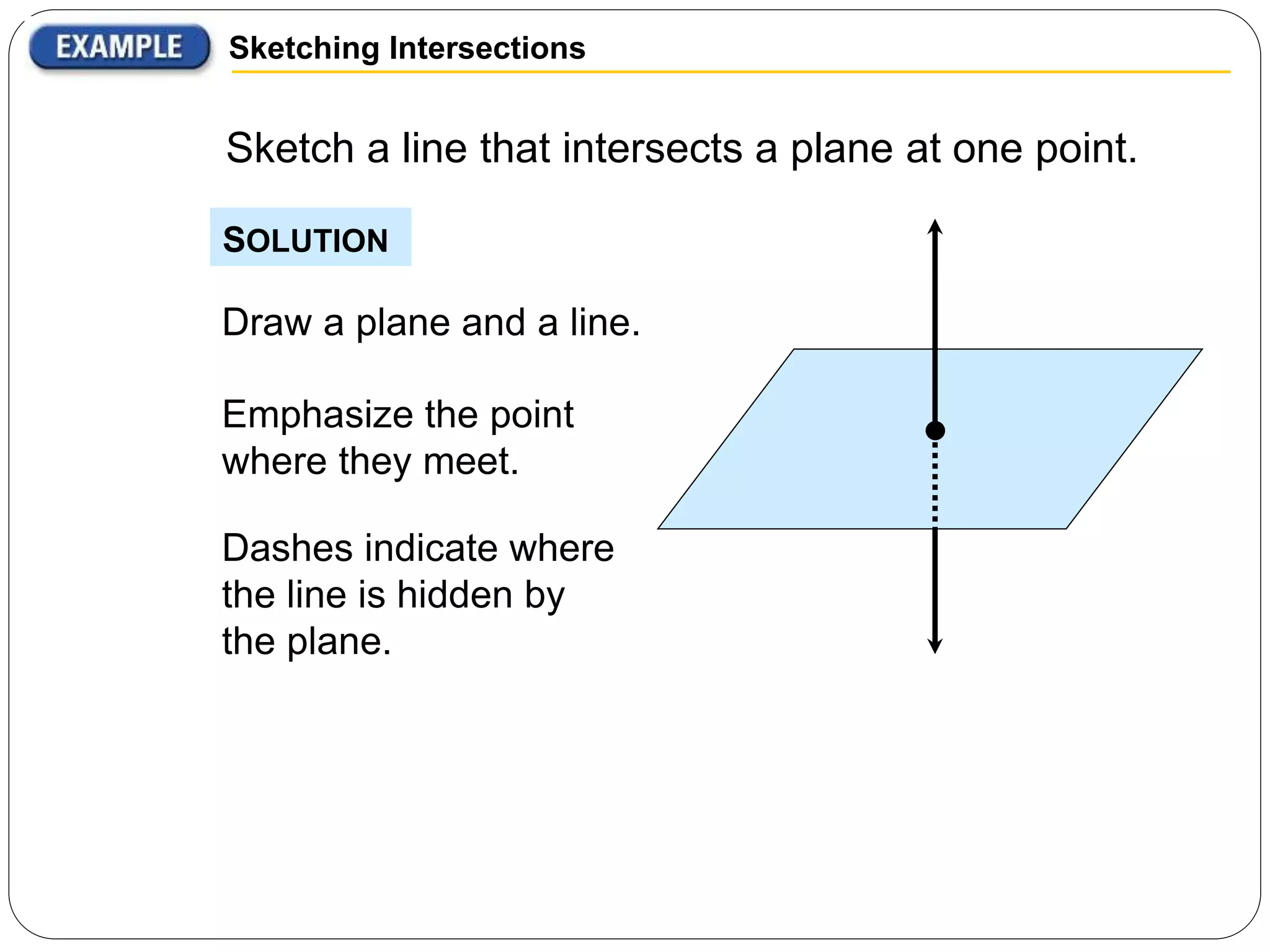
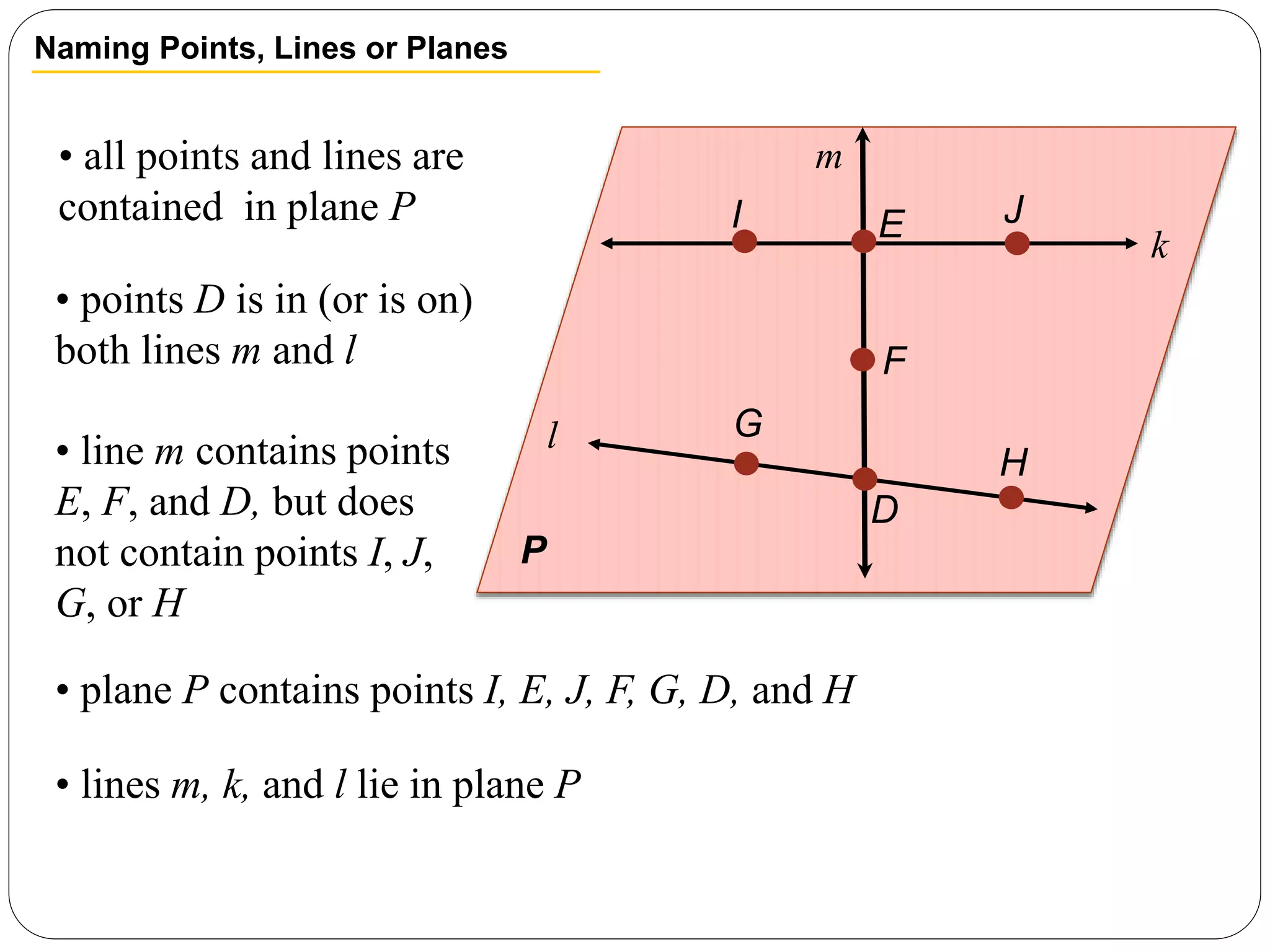
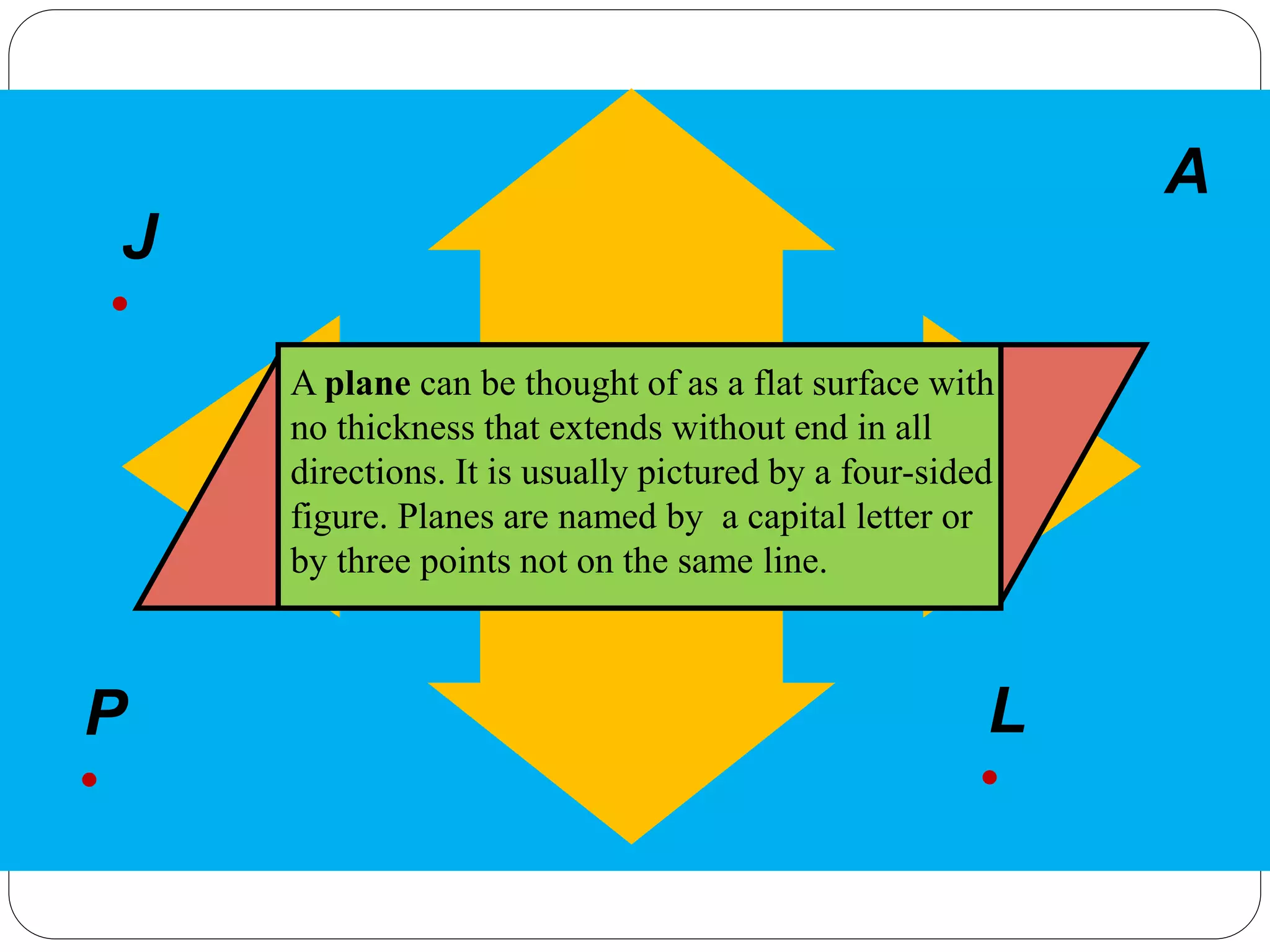
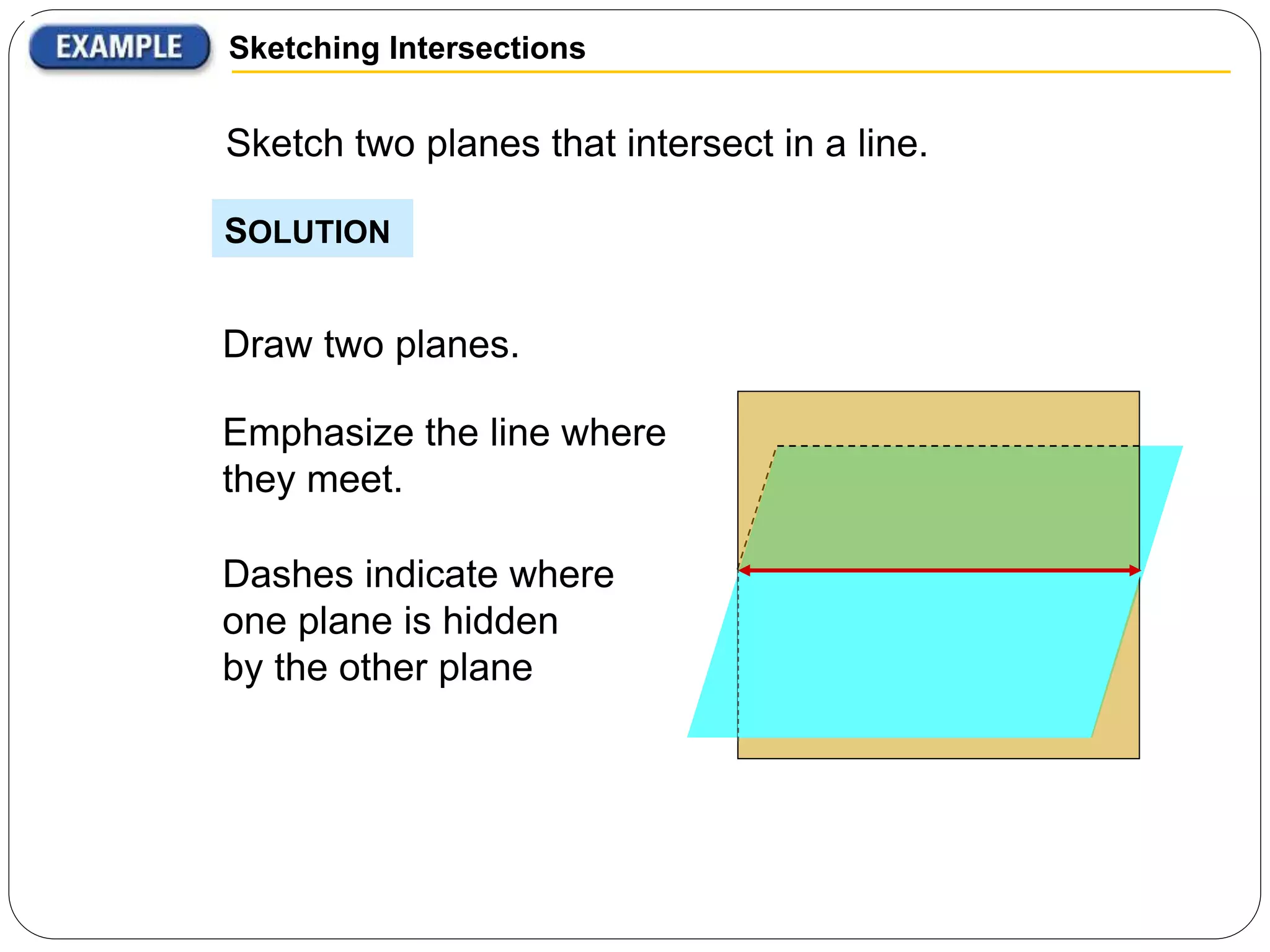
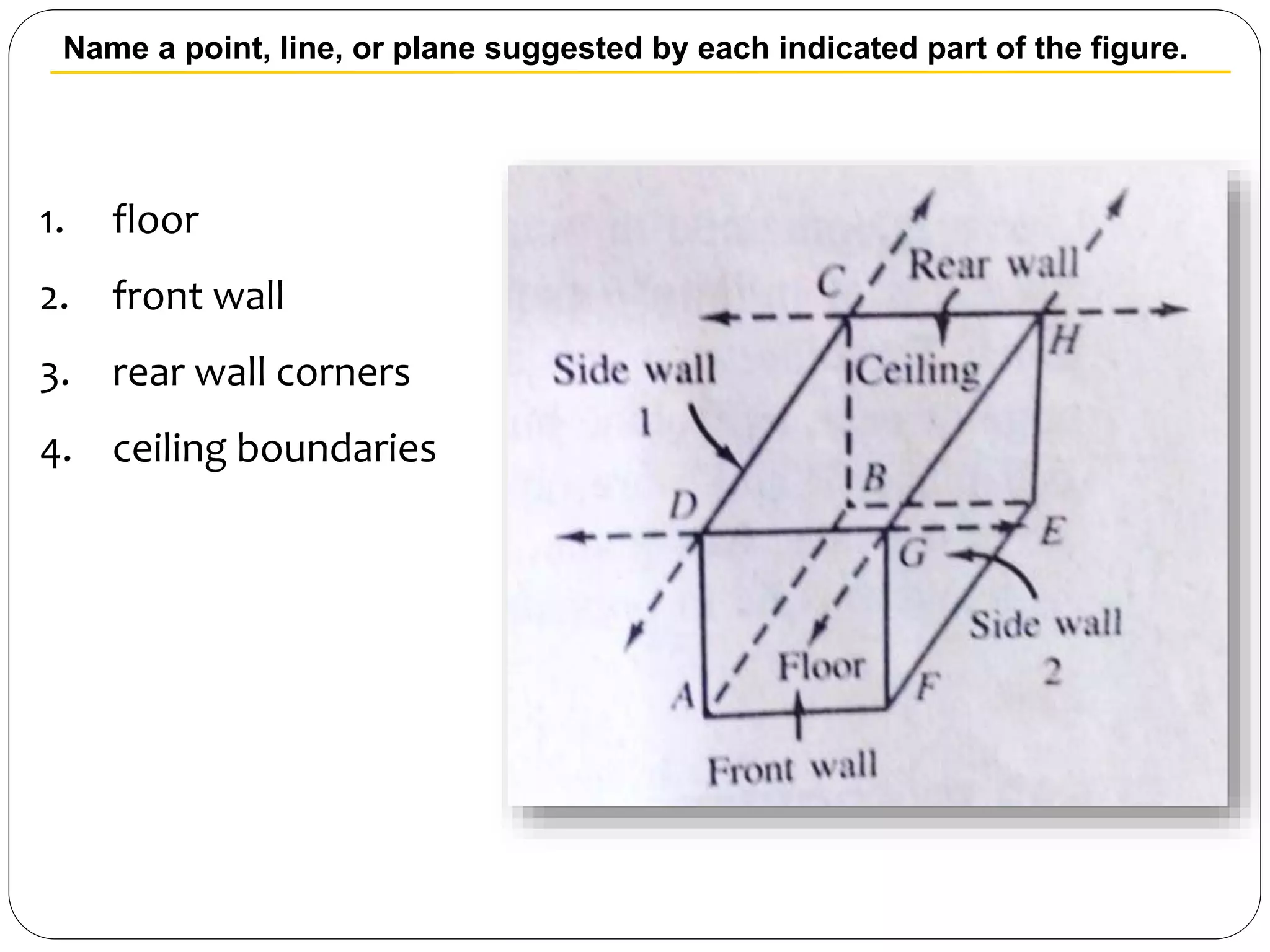
This document introduces basic geometric concepts including points, lines, and planes. It defines these terms and provides examples of representing them visually. Key points covered include: - A point has no dimension and is represented by a dot. - A line consists of infinitely many points and is shown as an arrowed line. - A plane is a flat, thickness-less surface that extends indefinitely in all directions and is usually pictured as a four-sided shape. 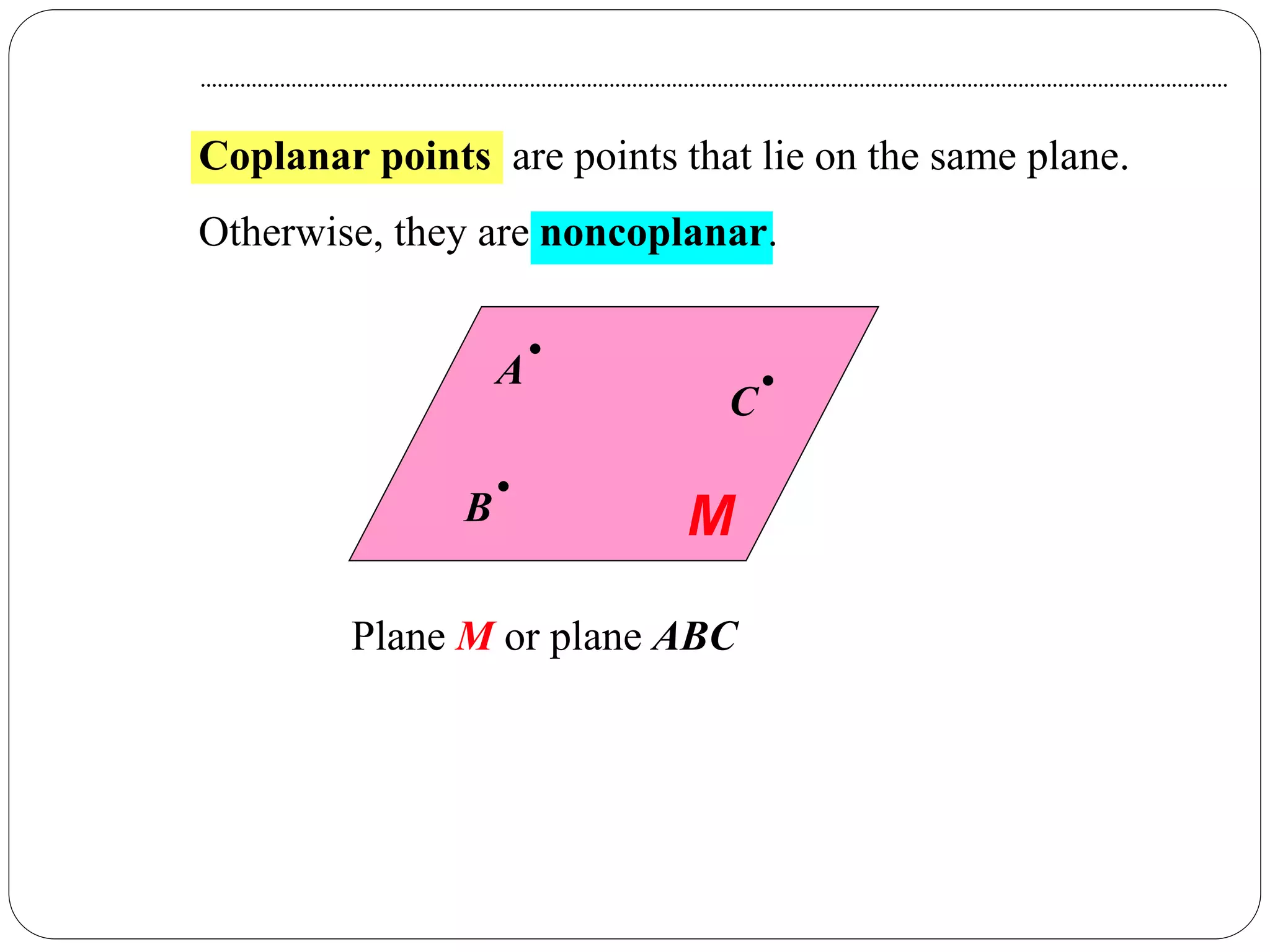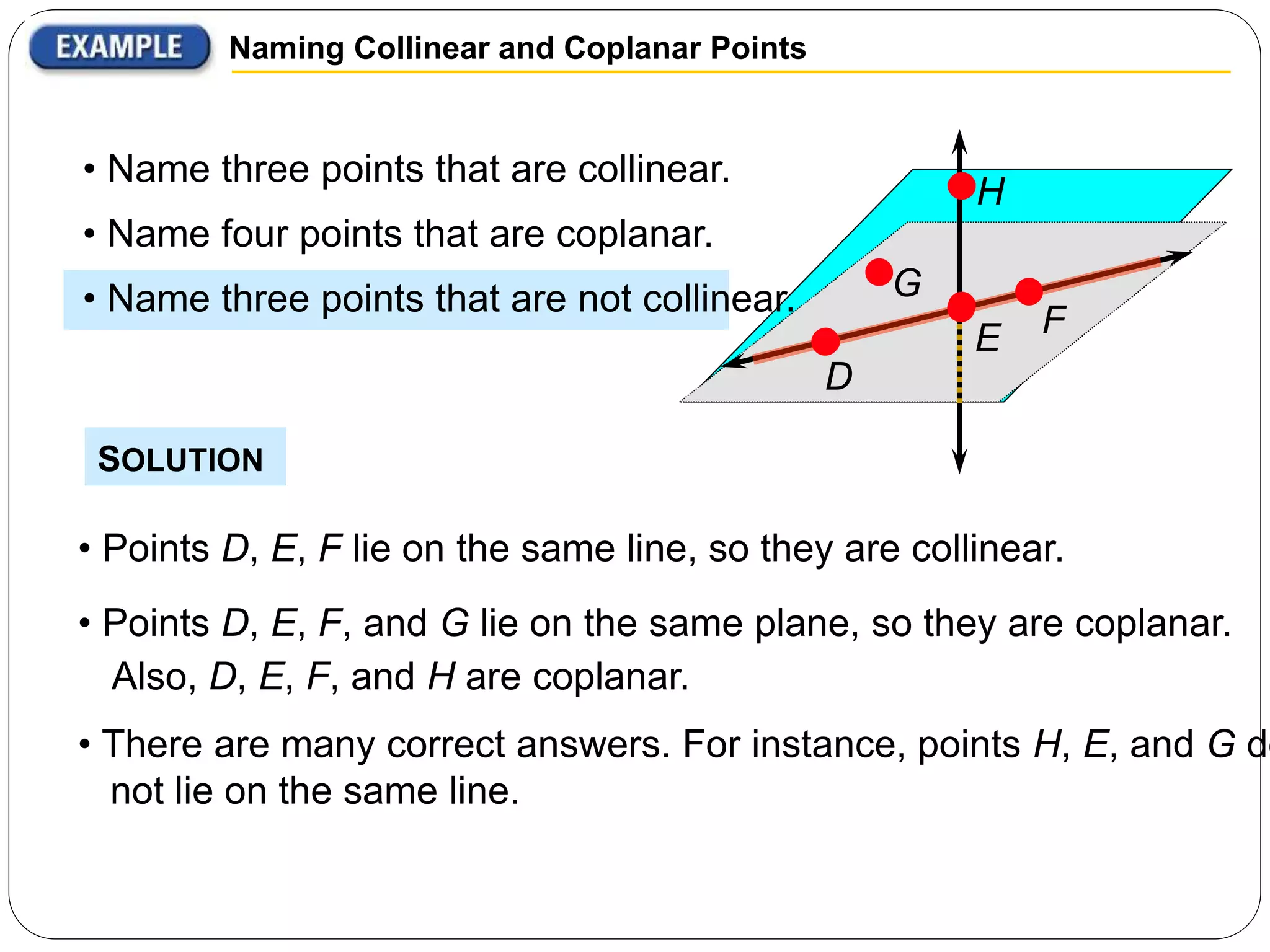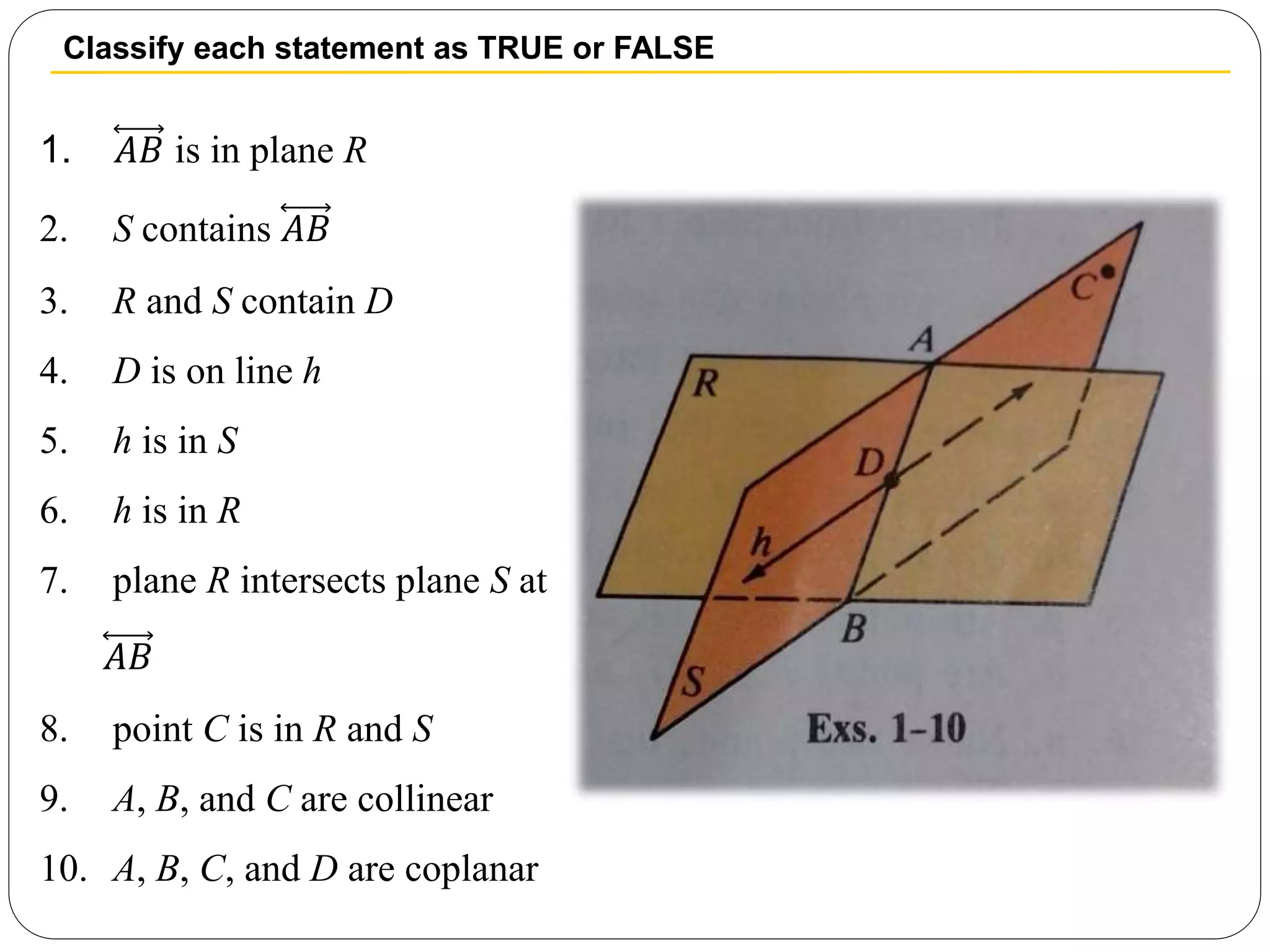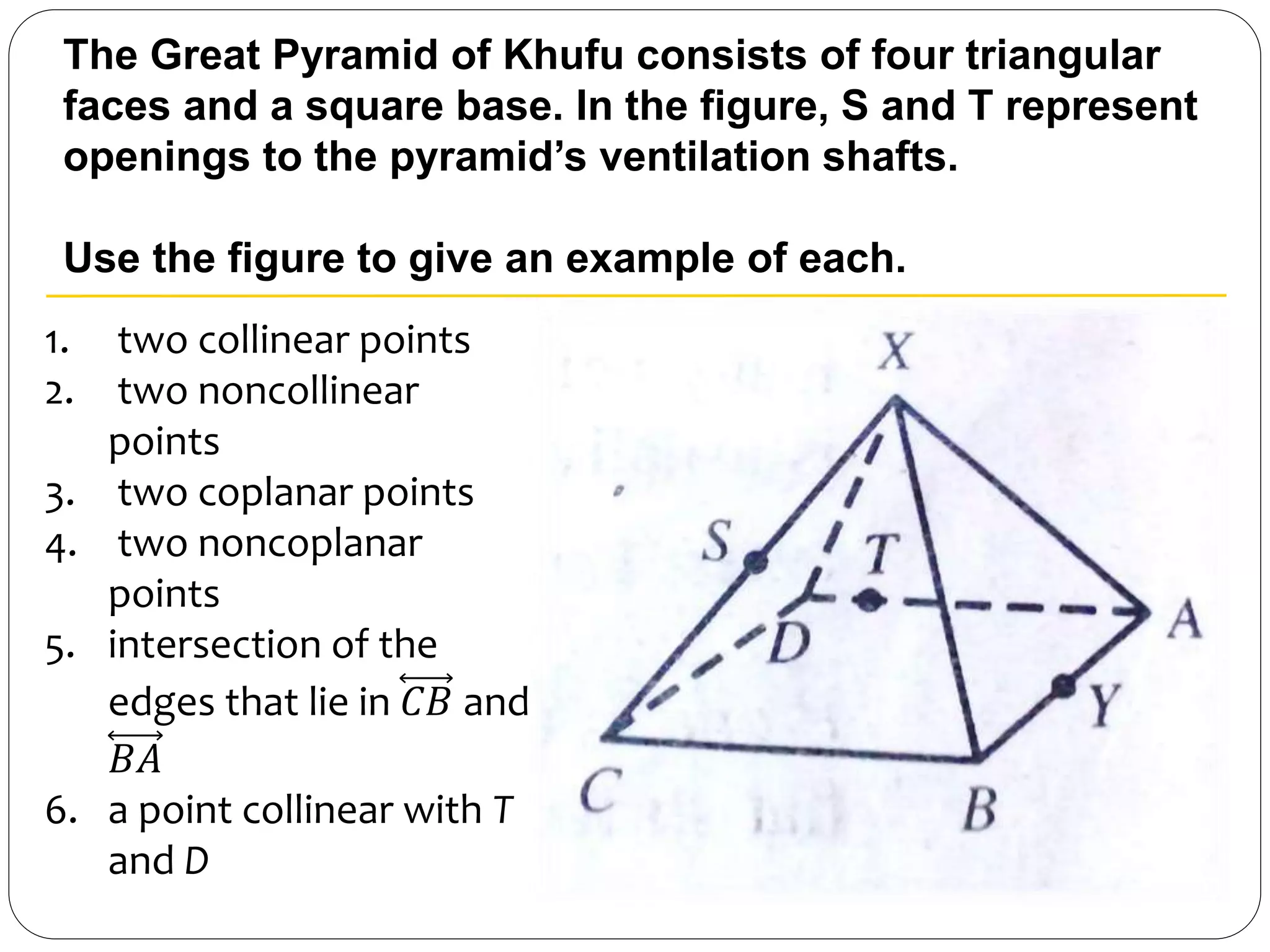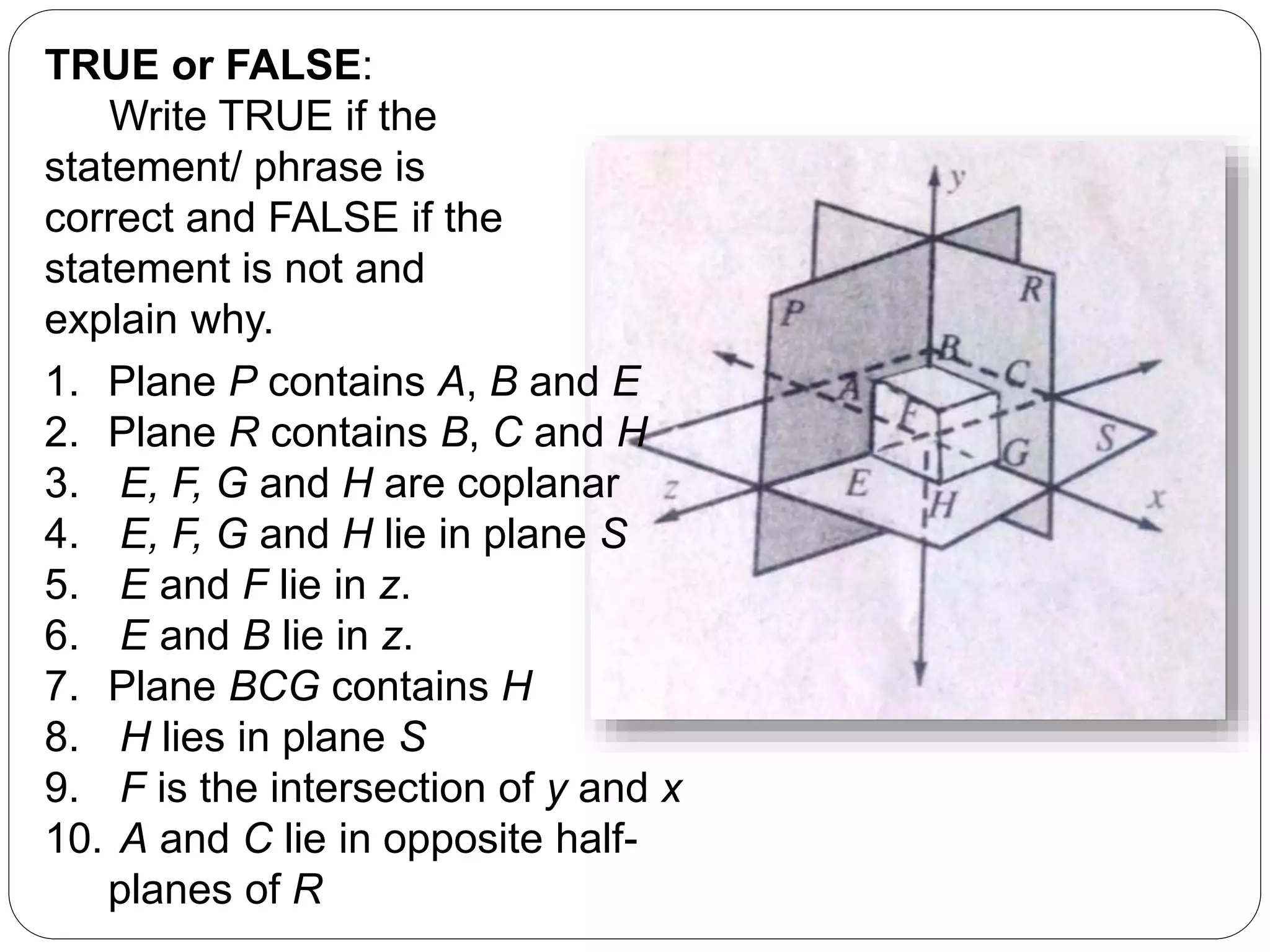- Coplanar and collinear points are defined in relation to lying on the same plane or line, respectively.

1. Language of
Geometry

2. GOALS
 Identify and draw representations of points,
lines and planes
 Use undefined terms to define some basic
geometric terms

3. PROBLEM POSING:
When you look at the night sky how many stars do
you see?
INVESTIGATION…
The bright stars at the
right form the constellation,
the Big Dipper. You can think
of the stars as points. Copy
and trace the points. Connect
the points with lines to
illustrate the constellation.

4. A point has no dimension.
It is usually represented by a small dot.
•A
Point A
It is named with a capital letter.

5. A line consists of infinitely many points. It is usually
represented by a straight line with two arrowheads to
indicate that the line extends without end in two directions.
Line or AB
Points are collinear if and only if they lie on the same line.
1. Points are collinear if they lie on the same line.
2. Points lie on the same line if they are collinear.

6. A line consists of infinitely many points. It is usually
represented by a straight line with two arrowheads to
indicate that the line extends without end in two directions.
Line or AB
Points are collinear if and only if they lie on the same line.
Points that are not collinear are called noncollinear.

7. A plane can be thought of as a flat surface with
no thickness that extends without end in all
directions. It is usually pictured by a four-sided
figure. Planes are named by a capital letter or
by three points not on the same line.
J
•
P
•
L
•
A

8. Coplanar points are points that lie on the same plane.
Otherwise, they are noncoplanar.
Plane M or plane ABC
A
C
MB

9. Space is the set of all points. A set of points is
the intersection of two figures if and only if the
points lie in both figures. The figures intersect at
that point or set of points.

10. Sketching Intersections
Sketch a line that intersects a plane at one point.
SOLUTION
Draw a plane and a line.
Emphasize the point
where they meet.
Dashes indicate where
the line is hidden by
the plane.

11. Sketch two planes that intersect in a line.
Sketching Intersections
SOLUTION
Draw two planes.
Emphasize the line where
they meet.
Dashes indicate where
one plane is hidden
by the other plane

12. Naming Collinear and Coplanar Points
SOLUTION
• Points D, E, F lie on the same line, so they are collinear.
• There are many correct answers. For instance, points H, E, and G do
not lie on the same line.
• Points D, E, F, and G lie on the same plane, so they are coplanar.
Also, D, E, F, and H are coplanar.
G
H
FE
D
• Name three points that are collinear.
• Name four points that are coplanar.
• Name three points that are not collinear.

13. D
l
k
G
H
I
F
JE
m
P
Naming Points, Lines or Planes
• all points and lines are
contained in plane P
• points D is in (or is on)
both lines m and l
• line m contains points
E, F, and D, but does
not contain points I, J,
G, or H
• plane P contains points I, E, J, F, G, D, and H
• lines m, k, and l lie in plane P

14. Classify each statement as TRUE or FALSE
1. 𝐴𝐵 is in plane R
2. S contains 𝐴𝐵
3. R and S contain D
4. D is on line h
5. h is in S
6. h is in R
7. plane R intersects plane S at
𝐴𝐵
8. point C is in R and S
9. A, B, and C are collinear
10. A, B, C, and D are coplanar

16. Name a point, line, or plane suggested by each indicated part of the figure.
1. floor
2. front wall
3. rear wall corners
4. ceiling boundaries

17. The Great Pyramid of Khufu consists of four triangular
faces and a square base. In the figure, S and T represent
openings to the pyramid’s ventilation shafts.
Use the figure to give an example of each.
1. two collinear points
2. two noncollinear
points
3. two coplanar points
4. two noncoplanar
points
5. intersection of the
edges that lie in 𝐶𝐵 and
𝐵𝐴
6. a point collinear with T
and D

19. TRUE or FALSE:
Write TRUE if the
statement/ phrase is
correct and FALSE if the
statement is not and
explain why.
1. Plane P contains A, B and E
2. Plane R contains B, C and H
3. E, F, G and H are coplanar
4. E, F, G and H lie in plane S
5. E and F lie in z.
6. E and B lie in z.
7. Plane BCG contains H
8. H lies in plane S
9. F is the intersection of y and x
10. A and C lie in opposite half-
planes of R