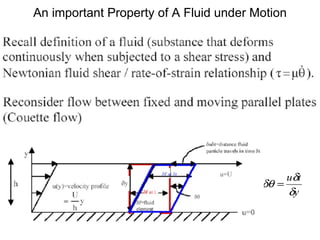
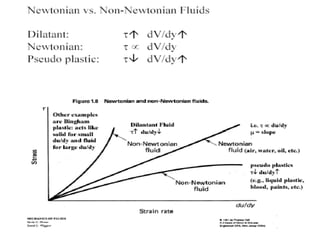
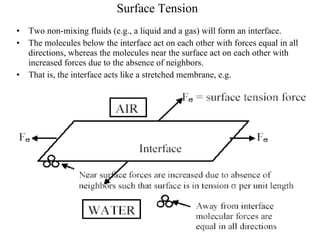
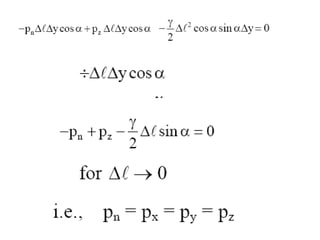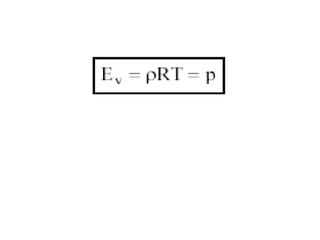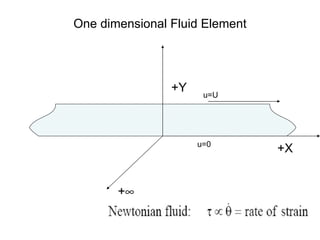
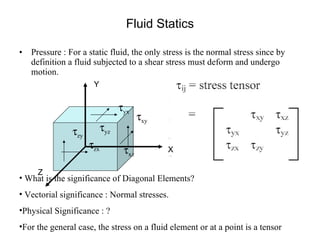
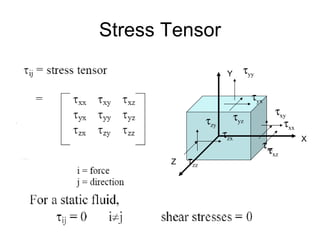
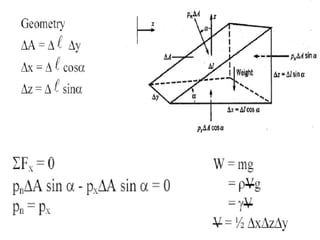
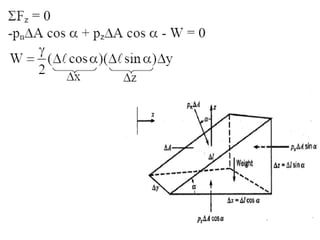
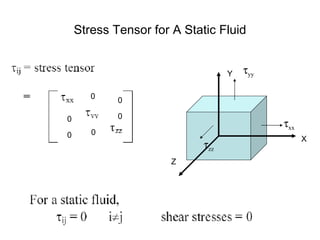
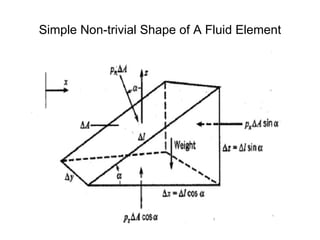
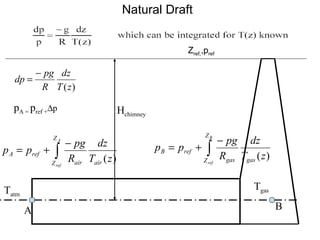
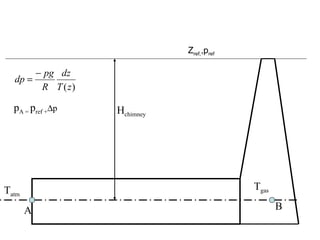
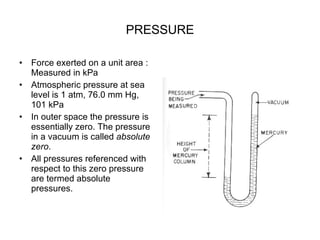
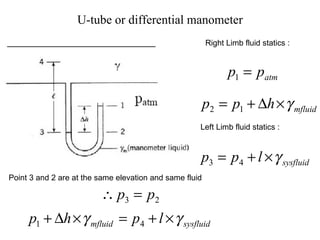
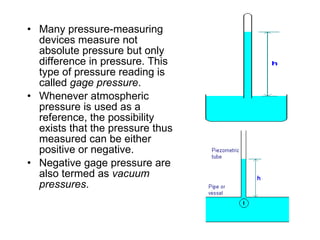
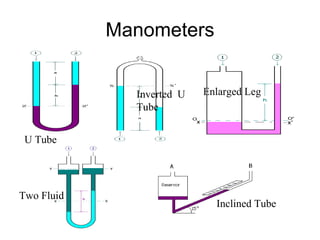
The document discusses several key properties of fluids relevant for fluid mechanics, including: 1) Fluids can be modeled as continua when the number of molecules is sufficiently large at any point. 2) For static fluids, the only stress is normal stress since shear stress would induce motion. 3) Pressure in static fluids varies only with elevation and is constant at any horizontal plane. 4) Pressure measurement devices like manometers use fluid statics principles to determine pressure differences.

1. Properties of Fluids for Fluid Mechanics P M V Subbarao Associate Professor Mechanical Engineering Department IIT Delhi Basic Steps to Design………….

2. Continuum Hypothesis In this course, the assumption is made that the fluid behaves as a continuum, i.e., the number of molecules within the smallest region of interest (a point) are sufficient that all fluid properties are point functions (single valued at a point). For example: Consider definition of density ρ of a fluid δV* = limiting volume below which molecular variations may be important and above which macroscopic variations may be important.

3. Static Fluid For a static fluid Shear Stress should be zero. For A generalized Three dimensional fluid Element, Many forms of shear stress is possible.

4. One dimensional Fluid Element +X +  +Y u=0 u=U

5. Fluid Statics Pressure : For a static fluid, the only stress is the normal stress since by definition a fluid subjected to a shear stress must deform and undergo motion. What is the significance of Diagonal Elements? Vectorial significance : Normal stresses. Physical Significance : ? For the general case, the stress on a fluid element or at a point is a tensor X Y Z  xy  xz  yz  yx  zx  zy

6. Stress Tensor X Y Z  yy  zz  yz  yx  zx  zy  xx  xy  xz  xz

7. First Law of Pascal Proof ?

8. Simple Non-trivial Shape of A Fluid Element

16. Fluid Statics for Power Generation P M V Subbarao Associate Professor Mechanical Engineering Department IIT Delhi Steps for Design of Flow Devices………….

17. Pressure Variation with Elevation For a static fluid, pressure varies only with elevation within the fluid. This can be shown by consideration of equilibrium of forces on a fluid element Basic Differential Equation: Newton's law (momentum principle) applied to a static fluid Σ F = ma = 0 for a static fluid i.e., Σ Fx = Σ Fy = Σ Fz = 0 1st order Taylor series estimate for pressure variation over dz

19. For a static fluid, the pressure only varies with elevation z and is constant in horizontal xy planes. The basic equation for pressure variation with elevation can be integrated depending on whether ρ = constant i.e., the fluid is incompressible (liquid or low-speed gas) or ρ = ρ (z), or compressible (high-speed gas) since g is constant.

20. Pressure Variation for a Uniform-Density Fluid

22. Reading Material Fluid Mechanics – Frank M White, McGraw Hill International Editions. Introduction to Fluid Mechanics – Fox & McDOnald, John Wiley & Sons, Inc. Fluid Mechanics – V L Streeter, E Benjamin Wylie & K W Bedfore, WCB McGraw Hill. Fluid Mechanics – P K Kundu & I M Cohen, Elsevier Inc.

23. Pressure Variation for Compressible Fluids Basic equation for pressure variation with elevation Pressure variation equation can be integrated for γ (p,z) known. For example, here we solve for the pressure in the atmosphere assuming ρ (p,T) given from ideal gas law, T(z) known, and g ≠ g(z).

25. Draft Required to Establish Air Flow Air in Flue gas out

26. Natural Draft H chimney T atm T gas A B p A = p ref +  p Z ref, ,p ref

28. H chimney T atm T gas A B p A = p ref +  p Z ref, ,p ref

29. Pressure variations in Troposphere: Linear increase towards earth surface T ref & p ref are known at Z ref .  Adiabatic Lapse rate : 6.5 K/km

30. Reference condition: At Z ref : T=T ref & p = p ref

31. Pressure at A: Pressure variation inside chimney differs from atmospheric pressure. The variation of chimney pressure depends on temperature variation along Chimney. Temperature variation along chimney depends on rate of cooling of hot gas Due to natural convection. Using principles of Heat transfer, one can calculate, T gas (Z). If this is also linear: T = T ref,gas +   (Z ref -Z). Lapse rate of gas,  gas is obtained from heat transfer analysis.

32. Natural Draft Natural Draft across the furnace,  p nat = p A – p B The difference in pressure will drive the exhaust. Natural draft establishes the furnace breathing by Continuous exhalation of flue gas Continuous inhalation of fresh air. The amount of flow is limited by the strength of the draft.

33. Pressure Measurement Another Application of Fluid Statics

34. Pressure Measurement Pressure is an important variable in fluid mechanics and many instruments have been devised for its measurement. Many devices are based on hydrostatics such as barometers and manometers, i.e., determine pressure through measurement of a column (or columns) of a liquid using the pressure variation with elevation equation for an incompressible fluid.

35. PRESSURE Force exerted on a unit area : Measured in kPa Atmospheric pressure at sea level is 1 atm, 76.0 mm Hg, 101 kPa In outer space the pressure is essentially zero. The pressure in a vacuum is called absolute zero . All pressures referenced with respect to this zero pressure are termed absolute pressures.

36. Many pressure-measuring devices measure not absolute pressure but only difference in pressure. This type of pressure reading is called gage pressure . Whenever atmospheric pressure is used as a reference, the possibility exists that the pressure thus measured can be either positive or negative. Negative gage pressure are also termed as vacuum pressures .

37. Manometers U Tube Inverted U Tube Enlarged Leg Two Fluid Inclined Tube

38. U-tube or differential manometer Right Limb fluid statics : Left Limb fluid statics : Point 3 and 2 are at the same elevation and same fluid

39. Gauge Pressure:

40. Absolute, Gauge & Vacuum Pressures System Pressure Atmospheric Pressure Gauge Pressure Absolute Pressure Absolute zero pressure

41. Absolute, Gauge & Vacuum Pressures System Pressure Atmospheric Pressure Vacuum Pressure Absolute Pressure Absolute zero pressure

42. Stress Tensor for A Static Fluid 0 0 0 0 0 0 X Y Z  yy  zz  xx

43. An important Property of A Fluid under Motion

44. Shear stress (  : Tangential force on per unit area of contact between solid & fluid

48. Elasticity (Compressibility) Increasing/decreasing pressure corresponds to contraction/expansion of a fluid. The amount of deformation is called elasticity.

51. Surface Tension Two non-mixing fluids (e.g., a liquid and a gas) will form an interface. The molecules below the interface act on each other with forces equal in all directions, whereas the molecules near the surface act on each other with increased forces due to the absence of neighbors. That is, the interface acts like a stretched membrane, e.g.

53. Vapour Pressure When the pressure of a liquid falls below the vapor pressure it evaporates, i.e., changes to a gas. If the pressure drop is due to temperature effects alone, the process is called boiling. If the pressure drop is due to fluid velocity, the process is called cavitation. Cavitation is common in regions of high velocity, i.e., low p such as on turbine blades and marine propellers.