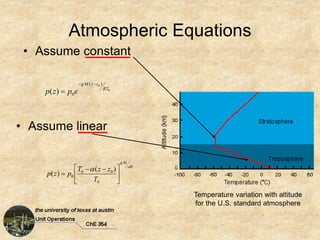
Okay, here are the steps to solve this problem: 1) Given: T0 = 15°C, P0 = 760 mm Hg = 101.325 kPa, dz = 1000 m 2) Temperature variation with elevation: dT/dz = -5°C/1000 m 3) Use ideal gas law: P1V1/T1 = P2V2/T2 4) Substitute values and solve for P2: P2 = P0(T0/T2) = 101.325(15/(15 - 5(8.847))) = 33.8 kPa So the air pressure on top of Mt. Everest at 8847 m is 33.

1. Fluid Statics

2. Definition of Pressure
Pressure is defined as the amount of force exerted on a
unit area of a substance:
Pa
m
N
area
force
P 

 2

3. Direction of fluid pressure on
boundaries
Furnace duct Pipe or tube
Heat exchanger
Dam
Pressure is a Normal Force
(acts perpendicular to surfaces)
It is also called a Surface Force

4. Absolute and Gauge Pressure
• Absolute pressure: The pressure of a fluid is expressed
relative to that of vacuum (=0)
• Gauge pressure: Pressure expressed as the difference
between the pressure of the fluid and that of the
surrounding atmosphere.
 Usual pressure guages record guage pressure. To
calculate absolute pressure:
gauge
atm
abs P
P
P 


5. Units for Pressure
Unit Definition or
Relationship
1 pascal (Pa) 1 kg m-1 s-2
1 bar 1 x 105 Pa
1 atmosphere (atm) 101,325 Pa
1 torr 1 / 760 atm
760 mm Hg 1 atm
14.696 pounds per
sq. in. (psi)
1 atm

6. Pressure distribution for a fluid at rest
Let’s determine the pressure
distribution in a fluid at rest
in which the only body force
acting is due to gravity
The sum of the forces acting
on the fluid must equal zero

7. mg zg
S
 
x
y
z
Let Pz and Pz+z denote the
pressures at the base and
top of the cube, where the
elevations are z and z+z
respectively.
What are the z-direction forces?
z
PS
z
z
PS 


8. Pressure distribution for a fluid at rest
zg
S
PS
PS
F z
z
z
z 



 

 
0
g
z
P
P z
z
z







A force balance in the z direction gives:
For an infinitesimal element (z0)
g
dz
dP




9. Incompressible fluid
Liquids are incompressible i.e. their density is assumed to
be constant:
By using gauge pressures we can simply write:
Po is the pressure at the
free surface (Po=Patm)
When we have a liquid with a free surface the pressure P
at any depth below the free surface is:
)
z
z
(
g
P
P 1
2
1
2 




P
gh
P o



gh
P 


10. Static pressure is a concern !!!!!

11. Static pressure - 10 minute problem:
Rainwater collects behind the concrete retaining wall shown below.
If the water-saturated soil (specific gravity = 2.2) acts as a fluid,
determine the force and center of pressure on a one-meter width of wall.
Water
Soil 3m
1m

12. Buoyancy
• A body immersed in a fluid experiences a vertical buoyant
force equal to the weight of the fluid it displaces
• A floating body displaces its own weight in the fluid in
which it floats
Free liquid surface
The upper surface of the body is
subjected to a smaller force than
the lower surface
 A net force is acting upwards
F1
F2
h1
h
2
H

13. Buoyancy
The net force due to pressure in the vertical direction is:
FB = F2- F1 = (Pbottom - Ptop) (xy)
The pressure difference is:
Pbottom – Ptop =  g (h2-h1) =  g H
Combining:
FB =  g H (xy)
Thus the buoyant force is:
FB =  g V

14. Measurement of Pressure
Manometers are devices in which one or
more columns of a liquid are used to
determine the pressure difference
between two points.
–U-tube manometer
–Inclined-tube manometer

15. Measurement of Pressure Differences
m
a
m
b
b
m
m
b
a
gR
Z
g
P
P
R
Z
g
P
P









)
(
)
(
3
2
Apply the basic equation of static
fluids to both legs of manometer,
realizing that P2=P3.
)
( b
a
m
b
a gR
P
P 
 



16. Inclined Manometer
• To measure small pressure differences need to magnify
Rm some way.


 sin
)
(
1 b
a
b
a gR
P
P 



17. Manometer - 10 minute problem
A simple U-tube manometer is installed across an orifice plate. The
manometer is filled with mercury (specific gravity = 13.6) and the
liquid above the mercury is water. If the pressure difference across
the orifice is 24 psi, what is the height difference (reading) on the
manometer in inches of mercury ?

18. Compressible Flow:
Natural gas well
Tall Mountains

19. Compressible fluid
• Gases are compressible i.e. their density varies with
temperature and pressure  =P M /RT
– For small elevation changes (as in engineering
applications, tanks, pipes etc) we can neglect the
effect of elevation on pressure
– In the general case start from:





 




o
o
RT
z
z
M
g
P
P
T
for
)
(
exp
:
const
T
1
2
1
2
g
dz
dP




20. Compressible
Linear Temperature Gradient
)
( 0
0 z
z
T
T 

 

 



z
z
p
p
z
z
T
dz
R
M
g
p
dp
0
0
)
( 0
0 
R
M
g
T
z
z
T
p
z
p







 


0
0
0
0
)
(
)
(

21. Atmospheric Equations
• Assume linear
R
M
g
T
z
z
T
p
z
p







 


0
0
0
0
)
(
)
(
• Assume constant
0
0 )
(
0
)
( RT
z
z
M
g
e
p
z
p



Temperature variation with altitude
for the U.S. standard atmosphere

22. Compressible Isentropic
v
p
C
C
P
constant
P





 

1
1
y
P
P
T
T
1
1
1
























 







 















 







 



1
1
2
1
1
1
2
1
1
1
1
RT
z
gM
T
T
RT
z
gM
P
P







23. Compressible Fluid – 10 minute problem
The temperature of the earth’s surface drops about 5 C for every
1000 m of elevation above the earth’s surface. If the air temperature
at ground level is 15 C and the pressure is 760 mm Hg, what is the air
pressure on top of Mt. Everest at 8847 m ? Assume air behaves as
an ideal gas.