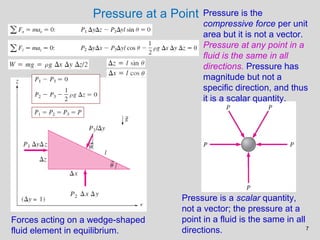
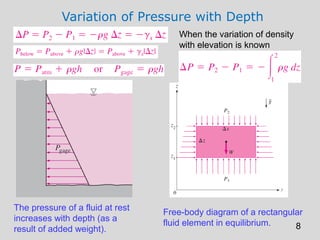
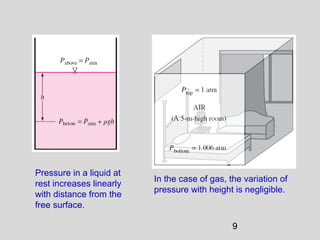
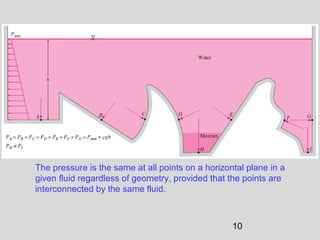
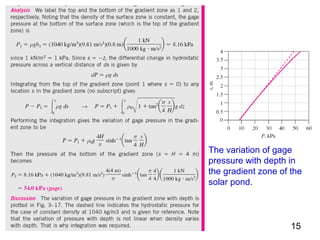
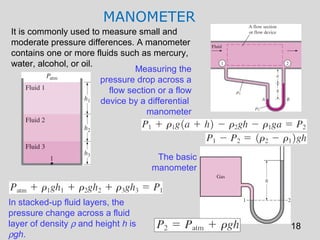
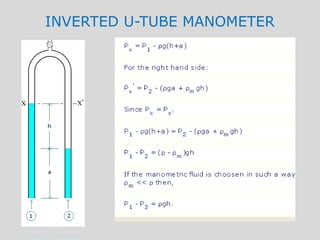
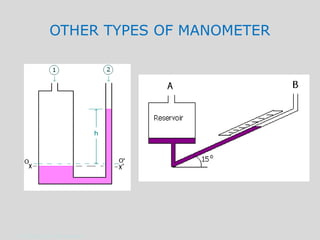
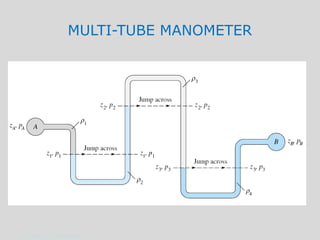
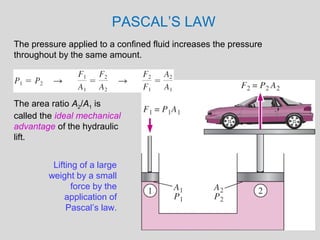
This document discusses pressure measurement and manometers. It begins by defining pressure and discussing absolute and gauge pressure. It then describes various pressure measurement devices like barometers, manometers, and pressure transducers. Manometers use fluid columns of different densities to measure pressure differences. U-tube, inverted U-tube, and multi-tube manometers are described. Pascal's law states that pressure increases uniformly in an incompressible fluid, and is used in hydraulic systems. Deadweight testers can precisely measure extremely high pressures.

1. FLUID MECHANICS – 1
First Semester 2011 - 2012
Week – 1
Class – 2
Pressure and Manometers
Compiled and modified
by
Sharma, Adam

2. Review
Introduction to Fluid mechanics
Concepts and definitions
Applications of fluid mechanics
Dimensions and Units
Basic dimensions in FM
Different units of measurement
Properties of fluids
Density and Relative density
Absolute and kinematic viscosity
2

3. OBJECTIVES
• Concept of pressure
• Pressure variation in a fluid at rest
• Pressure measuring devices
• Measurement of pressure using various kinds
of manometers
3

4. PRESSURE
Pressure: A normal force exerted
by a fluid per unit area
The normal stress (or “pressure”) on
the feet of a chubby person is much
Some basic greater than on the feet of a slim
pressure person.
gages. 4

5. Absolute pressure: The actual pressure at a given position. It
is measured relative to absolute vacuum (i.e., absolute zero
pressure).
Gage pressure: The difference between the absolute pressure
and the local atmospheric pressure. Most pressure-measuring
devices are calibrated to read zero in the atmosphere, and so
they indicate gage pressure.
Vacuum pressures: Pressures below atmospheric pressure.
5

6. 40 kPa
100 kPa
100 − 40 = 60 kPa
6

7. Pressure at a Point Pressure is the
compressive force per unit
area but it is not a vector.
Pressure at any point in a
fluid is the same in all
directions. Pressure has
magnitude but not a
specific direction, and thus
it is a scalar quantity.
Pressure is a scalar quantity,
not a vector; the pressure at a
Forces acting on a wedge-shaped point in a fluid is the same in all
fluid element in equilibrium. directions. 7

8. Variation of Pressure with Depth
When the variation of density
with elevation is known
The pressure of a fluid at rest
Free-body diagram of a rectangular
increases with depth (as a
fluid element in equilibrium. 8
result of added weight).

9. Pressure in a liquid at
In the case of gas, the variation of
rest increases linearly
pressure with height is negligible.
with distance from the
free surface.
9

10. The pressure is the same at all points on a horizontal plane in a
given fluid regardless of geometry, provided that the points are
interconnected by the same fluid.
10

11. PRESSURE MEASURING
DEVICES

12. PRESSURE MEASUREMENT DEVICES
The Barometer
• Atmospheric pressure is measured by a device called a barometer; thus,
the atmospheric pressure is often referred to as the barometric pressure.
• A frequently used pressure unit is the standard atmosphere, which is
defined as the pressure produced by a column of mercury 760 mm in
height at 0°C (ρHg = 13.595 kg/m3) under standard gravitational acceleration
(g = 9.807 m/s2).
The length or the
cross-sectional area
of the tube has no
effect on the height
of the fluid column of
a barometer,
provided that the
tube diameter is
large enough to
avoid surface tension
(capillary) effects.
The basic barometer. 12

13. 13

14. 14

15. The variation of gage
pressure with depth in
the gradient zone of the
solar pond.
15

16. MEASUREMENT OF PRESSURE
USING VARIOUS KINDS OF
MANOMETERS

17. PASCAL’S LAW
Pascal’s law: Any two points at the same elevation a
continuous mass of the same static fluid will be at the same
pressure.
The idea of jumping across to equal pressures facilitates
manometer calculations.
11-15 January 2010 M Subramanian

18. MANOMETER
It is commonly used to measure small and
moderate pressure differences. A manometer
contains one or more fluids such as mercury,
water, alcohol, or oil.
Measuring the
pressure drop across a
flow section or a flow
device by a differential
manometer
The basic
manometer
In stacked-up fluid layers, the
pressure change across a fluid
layer of density ρ and height h is 18
ρgh.

19. MANOMETER CALCULATIONS
Simple U-tube manometer
11-15 January 2010 M Subramanian

20. INVERTED U-TUBE MANOMETER
11-15 January 2010 M Subramanian

21. OTHER TYPES OF MANOMETER
11-15 January 2010 M Subramanian

22. MULTI-TUBE MANOMETER
11-15 January 2010 M Subramanian

23. 23

24. 24

25. 25

26. OTHER PRESSURE MEASUREMENT DEVICES
• Bourdon tube: Consists of a hollow metal tube
bent like a hook whose end is closed and
connected to a dial indicator needle.
• Pressure transducers: Use various techniques
to convert the pressure effect to an electrical
effect such as a change in voltage, resistance,
or capacitance.
• Pressure transducers are smaller and faster,
and they can be more sensitive, reliable, and
precise than their mechanical counterparts.
• Strain-gage pressure transducers: Work by
having a diaphragm deflect between two
chambers open to the pressure inputs. Pressure transducers
• Piezoelectric transducers: Also called solid-state
pressure transducers, work on the principle that
an electric potential is generated in a crystalline
substance when it is subjected to mechanical
pressure.
26
Piezoelectric pressure transducers

27. PASCAL’S LAW
The pressure applied to a confined fluid increases the pressure
throughout by the same amount.
The area ratio A2/A1 is
called the ideal mechanical
advantage of the hydraulic
lift.
Lifting of a large
weight by a small
force by the
application of
Pascal’s law.
27

28. Deadweight tester: Another type of mechanical pressure gage. It is used
primarily for calibration and can measure extremely high pressures.
A deadweight tester measures pressure directly through application of a
weight that provides a force per unit area—the fundamental definition of
pressure.
It is constructed with an internal chamber filled with a fluid (usually oil),
along with a tight-fitting piston, cylinder, and plunger.
Weights are applied to the top of the piston, which exerts a force on the oil
in the chamber. The total force F acting on the oil at the piston–oil interface
is the sum of the weight of the piston plus the applied weights.
A deadweight tester is able to measure
extremely high pressures (up to 70 MPa in 28
some applications).

29. Any Questions?
11-15 January 2010 M Subramanian