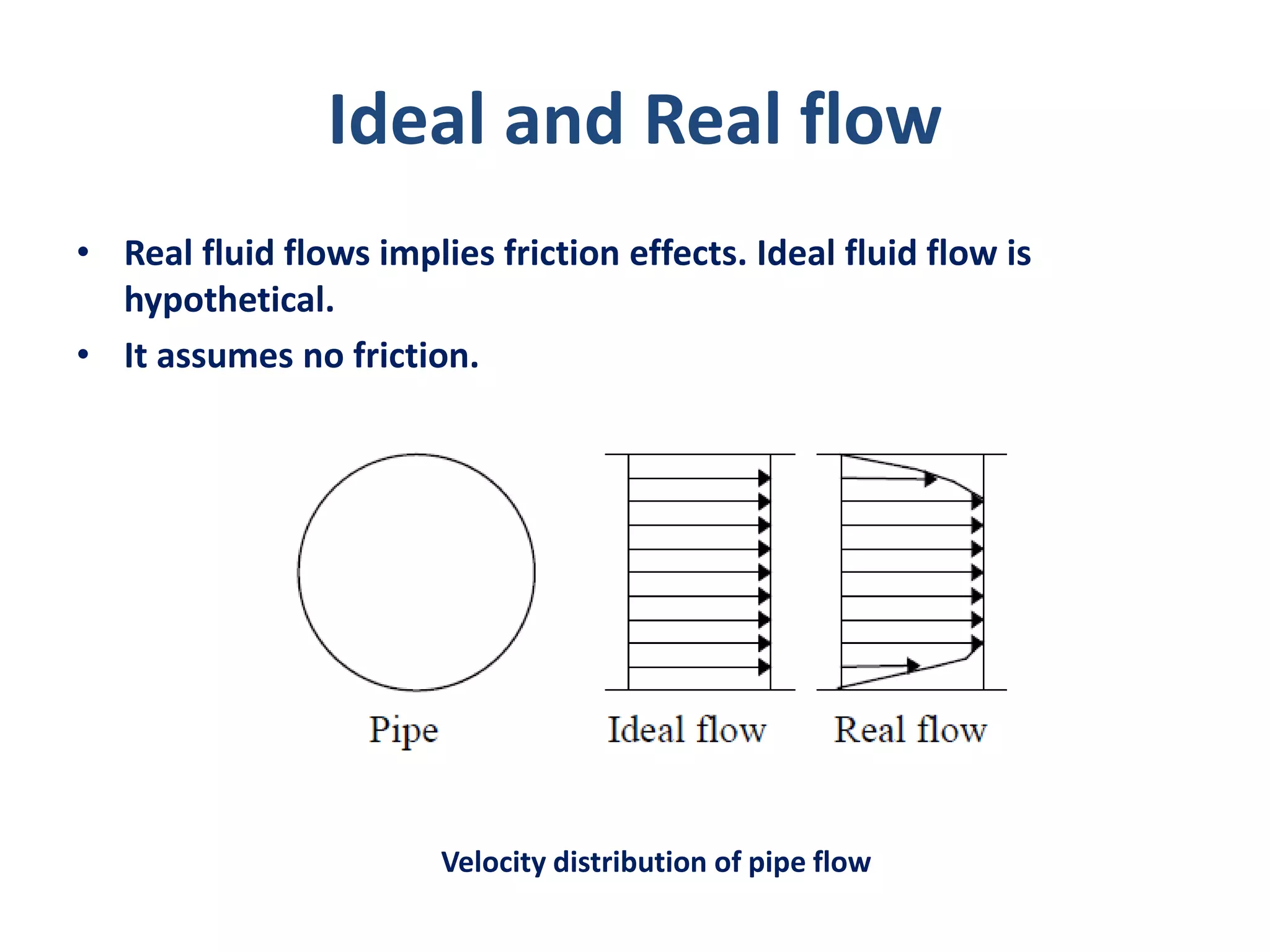
This document discusses fluid kinematics, which is the branch of fluid mechanics that deals with the geometry and motion of fluids without considering forces. It defines key concepts like acceleration fields, Lagrangian and Eulerian methods of describing motion, types of flow such as laminar vs turbulent and steady vs unsteady, streamlines vs pathlines vs streaklines, circulation and vorticity, and analytical tools like the stream function and velocity potential function. Flow nets are introduced as a way to graphically study two-dimensional irrotational flows using a grid of intersecting streamlines and equipotential lines.

1. FLUID KINEMATICS
By – Shabin George

2. What is Fluid Kinematics ?
 Branch of fluid mechanics which deals with response of fluids in
motion without considering forces and energies in them.
 The study of kinematics is often referred to as the geometry of
motion.
 It is generally a continuous function in space and time.

3. Acceleration Field
 The acceleration of the particle is ascribable to two reasons.
 One reason is due to the fluid particle being convected from one
given location to another location in flow and the second location
being of higher or lower velocity.
 This is called as convective acceleration. It is also known as
advective acceleration.
 The second reason is due to the unsteadiness of the flow, that is
due to the change in the local velocity of the fluid particle as a
function of time. This is called as local acceleration.

5. Methods of describing Fluid
Motion
 Langrangian Method :
 It describes a defined mass (position, velocity, acceleration,
temperature , pressure, etc) as functions of time.
 Eg. Track the location of a migrating bird.
 Eulerian Method :
 It describes the flow field ( velocity, acceleration, pressure,
temperature, etc. ) as functions of position and time.
 Eg. Ounting the birds passing a particular location.

6. Types of Flow
 Depending upon fluid properties
 Ideal and Real flow.
 Compressible and Incompressible flow.
 Depending upon properties of flow
 Laminar and turbulent flow.
 Steady and unsteady flow.
 Uniform and Non-uniform flow.
 Rotational and Irrotational flow.
 One, two and three dimensional flow.

7. Ideal and Real flow
• Real fluid flows implies friction effects. Ideal fluid flow is
hypothetical.
• It assumes no friction.
Velocity distribution of pipe flow

8. Compressible and Incompressible
flows
 Incompressible fluid flows assumes the fluid have constant
density while in compressible fluid flow, density is variable and
becomes function of temperature and pressure.

9. Laminar and turbulent flow
The flow in which adjacent
layer do not cross to each
other and move along the
well define path is called as
laminar flow.
Laminar flow
Turbulent flow
Transition of flow from Laminar to turbulent
Reynold’s number is used to
differentiate between laminar and
turbulent flows.

11. Steady and Unsteady flows
 Steady flow:
It is the flow in which conditions of flow remains
constant w.r.t. time at a particular section but the
condition may be different at different sections.
Flow conditions: velocity, pressure, density or
cross-sectional area etc.
e.g., A constant discharge through a pipe.
 Unsteady flow :
It is the flow in which conditions of flow changes
w.r.t. time at a particular section.
e.g. A variable discharge through a pipe.

12. Uniform and Non-uniform flow
 Uniform flow:
 The flow in which velocity at a given time
does not change with respect to space (length
of direction of flow) is called as uniform flow.
 e.g. Constant discharge though a constant
diameter pipe.
 Non – Uniform flow :
 The flow in which velocity at a given time
changes with respect to space (length of
direction of flow) is called as non – uniform
flow.
 e.g., Constant discharge through variable
diameter pipe.

13. Rotational & Irrotational Flow
 Rotational Flows :-
 The flow in which fuid particle while flowing
along stream lines rotate about their own axis is
called as rotational flow.
 Irrotational Flows:-
 The flow in which the fluid particle while
flowing along stream lines do not rotate about
their axis is called as irrotational flow.

14. One, Two and Three Dimensional
Flows
 Although in general all fluids flow three-dimensionally, with pressures
and velocities and other flow properties varying in all directions, in many
cases the greatest changes only occur in two directions or even only in
one. In these cases changes in the other direction can be effectively
ignored making analysis much more simple.
 Flow is one dimensional : if the flow parameters (such as velocity,
pressure, depth etc.) at a given instant in time only vary in the direction
of flow and not across the cross-section.

15. One, Two and Three Dimensional
Flows
 Flow is two-dimensional : if it can
be assumed that the flow parameters
vary in the direction of flow and in
one direction at right angles to this
direction.
 Flow is three-dimensional : if the
flow parameters vary in all three
direction of flow.

16. Visualization of flow Pattern
• The flow velocity is the basic description of how a fluid moves in
time and space, but in order to visualize the flow pattern it is
useful to define some other properties of the flow. These
definitions correspond to various experimental methods of
visualizing fluid flow. They are :
a. Streamlines
b. Pathlines
c. Streak lines
Flow around cylindrical object
CAR surface pressure contours
and streamlines

17. Visualization of flow Pattern
Streamlines around a wing shaped body
Flow around a skiing athlete

18. Stream line
A Streamline is a curve that is
everywhere tangent to the
instantaneous local velocity vector.
It has the direction of the velocity
vector at each point of flow across the
streamline.
Character of Streamline :
1. Streamlines can not cross each
other. (otherwise, the cross point
will have two tangential lines.)
2. Streamline can't be a folding line,
but a smooth curve.
3. Streamline cluster density reflects
the magnitude of velocity. (Dense
streamlines mean large velocity;
while sparse streamlines mean small
velocity.

19. PATHLINE
 A Pathline is the actual path
travelled by an individual fluid
particle over some time period.
 Same as the fluid particle's
material position vector .
 And the path of a particle
same as Streamline for Steady
Flow.

20. Streak line and Stream Tubes
 A streakline is the locus of
fluid particles that have passed
sequentially through a
prescribed point in the flow.
 Easy to generate in
experiments like dye in a water
flow, or smoke in an airflow.
Streamtube : is an imaginary
tube whose boundary
consists of streamlines.
The volume flow rate must
be the same for all cross
sections of the stream tube.

21. Circulation and Vorticity
 Circulation and vorticity are two primary measures of rotation in a
fluid.
 Circulation, which is a scalar integral quantity, is a macroscopic
measure of rotation for a finite area of the fluid.
 Vorticity however is a vector field that gives a microscopic measure of
the rotation at any point in the fluid.
VORTICITYCIRCULATION

22.  The circulation, C, about a closed contour in a fluid is defined as the
line integral evaluated along the contour of the component of the velocity
vector that is locally tangent to the contour.
“Meaning” of Circulation :
 Circulation can be considered as the amount of force that pushes along
a closed boundary or path. Circulation is the total “push” you get when
going along a path, such as a circle.
Circulation

23. Vorticity
 Vorticity is the tendency for elements of the fluid to spin.
 Vorticity can be related to the amount of circulation or rotation
(or more strictly the angular rate of rotation) in a fluid.
 Vertical Component of Vorticity :
 In large-scale dynamic meteorology, we are in concerned only
with the vertical components of absolute and relative vorticity.
 The vertical component of vorticity is defined as the circulation
about a closed contour in the horizontal plane divided by the area
enclosed, in the limit where the area approaches zero.

24. Stream Function
 It is defined as the scalar function of space and time, such that its
partial derivative with respect to any direction gives the velocity
component at right angles to that direction . It is denoted by psi
and defined for two dimensional flow.
 Properties of Stream Function :
i. If stream function exists, it is a possible case of fluid flow which
may be rotational or irrotational.
ii. If stream function satisfies the Laplace equation, it is a possible
case of an irrotational flow.
Laplace equation

25. Velocity Potential Function
 It is defined as a scalar function of space and time such that its
negative derivative with respect to any direction gives the fluid
velocity in that direction. It is denoted by phi.
 The negative sign indicates that the flow takes place in the direction
in which phi decreases.

28. Flow Net
 A grid obtained by drawing a series of stream lines and
equipotential lines is known as a flow net.
 Flow net provides a simple graphical technique for studying two –
dimensional irrotational flows, when the mathematical
calculation is difficult.
 The stream lines and equipotential lines are mutually
perpendicular to each other.
 A flow net analysis assist in the
design of an efficient boundary
shapes.
 It is also used to calculate the
flow at ground level.

29. THANK YOU!!