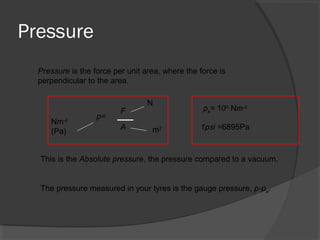
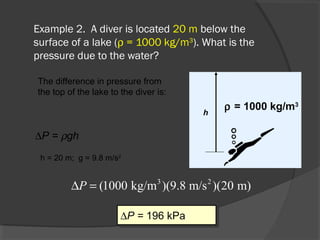
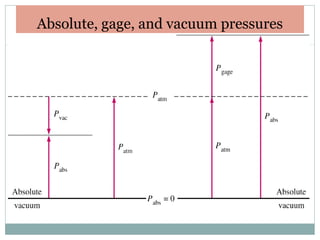
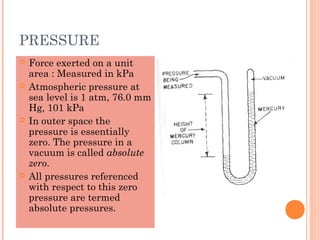
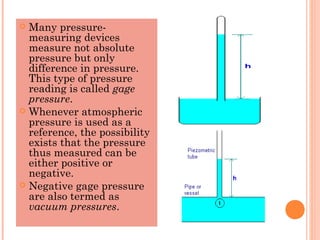
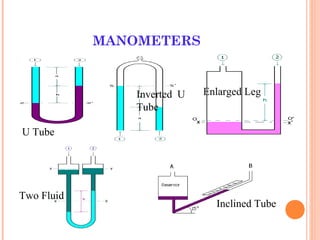
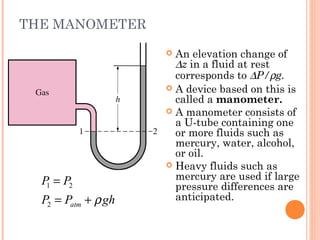
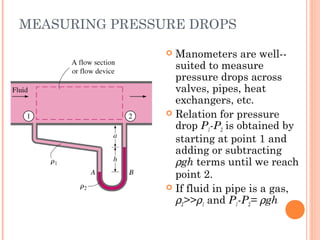
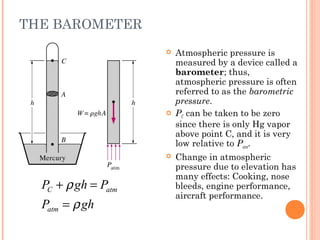
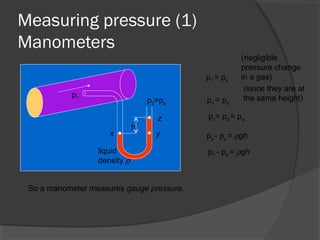
This document discusses fluid pressure and various ways to measure it. It defines pressure as a force per unit area and explains that pressure increases linearly with depth in a static fluid. It also describes how manometers and barometers work to measure pressure differences and atmospheric pressure respectively using the hydrostatic pressure equation. Manometers use columns of liquid like mercury or water, while barometers use a mercury column to directly measure atmospheric pressure at sea level.

1. CHAPTER 2: FLUIDPRESSURE
PREPARED BY :
NOOR ASSIKIN BINTI ABD WAHAB

2. Learn more about
Fluids
&
TODAY’S GOAL
PRESSURE

3. PRESSURE
 Pressure is defined as a normal force exerted by
a fluid per unit area.
 Units of pressure are N/m2
, which is called a
pascal (Pa).
 Since the unit Pa is too small for pressures
encountered in practice, kilopascal (1 kPa = 103
Pa) and megapascal (1 MPa = 106
Pa) are
commonly used.
 Other units include bar, atm, kgf/cm2
,
lbf/in2
=psi.

4. Pressure
Pressure is the force per unit area, where the force is
perpendicular to the area.
p=
A m2
Nm-2
(Pa)
N
F
This is the Absolute pressure, the pressure compared to a vacuum.
pa= 105
Nm-2
1psi =6895Pa
The pressure measured in your tyres is the gauge pressure, p-pa.

5. Pressure
Pressure in a fluid acts equally in all directions
Pressure in a static liquid increases linearly with depth
∆p=
increase in
depth (m)
pressure
increase
ρg ∆ h
The pressure at a given depth in a continuous, static body of liquid is
constant.
p1
p2
p3 p1 = p2 = p3

6. Pressure
Pressure is the ratio of a force F to the area A over which it is
applied:
Pressure ;
Force F
P
Area A
= =
A = 2 cm2
1.5 kg
2
-4 2
(1.5 kg)(9.8 m/s )
2 x 10 m
F
P
A
= =
P = 73,500 N/m2P = 73,500 N/m2

7. The Unit of Pressure (Pascal):
A pressure of one pascal (1 Pa) is defined as a force of one
newton (1 N) applied to an area of one square meter (1 m2
).
2
1 Pa = 1 N/mPascal:
In the previous example the pressure was 73,500
N/m2
. This should be expressed as:
P = 73,500 PaP = 73,500 Pa

8. PRESSURE HEAD
 P(A) static pressure of system
 Column of water supported by this pressure
 Pressure Head
 hp = p
ρg

9. Fluid exerts forces in many directions. Try to
submerse a rubber ball in water to see that an
upward force acts on the ball.
• Fluids exert pressure in all
directions.
F

10. Pressure vs. Depth in Fluid
Pressure = force/area
; ;
mg
P m V V Ah
A
ρ= = =
Vg Ahg
P
A A
ρ ρ
= =
h
mg
Area
• Pressure at any point in a
fluid is directly proportional
to the density of the fluid
and to the depth in the fluid.
P =
ρgh
Fluid Pressure:

11. Independence of Shape and
Area.
Water seeks its own level,
indicating that fluid pressure
is independent of area and
shape of its container.
• At any depth h below the surface of
the water in any column, the pressure
P is the same. The shape and area
are not factors.
• At any depth h below the surface of
the water in any column, the pressure
P is the same. The shape and area
are not factors.

12. PROPERTIES OF FLUID
PRESSURE
 The forces exerted by a fluid on the walls of
its container are always perpendicular.
 The fluid pressure is directly proportional to
the depth of the fluid and to its density.
 At any particular depth, the fluid pressure
is the same in all directions.
 Fluid pressure is independent of the shape
or area of its container.
 The forces exerted by a fluid on the walls of
its container are always perpendicular.
 The fluid pressure is directly proportional to
the depth of the fluid and to its density.
 At any particular depth, the fluid pressure
is the same in all directions.
 Fluid pressure is independent of the shape
or area of its container.

13. Example 2. A diver is located 20 m below the
surface of a lake (ρ = 1000 kg/m3
). What is the
pressure due to the water?
h
ρ = 1000 kg/m3
∆P = ρgh
The difference in pressure from
the top of the lake to the diver is:
h = 20 m; g = 9.8 m/s2
3 2
(1000 kg/m )(9.8 m/s )(20 m)P∆ =
∆P = 196 kPa∆P = 196 kPa

14. Atmospheric Pressure
at
m
at
m h
Mercury
P = 0
One way to measure atmospheric
pressure is to fill a test tube with
mercury, then invert it into a bowl
of mercury.
Density of Hg = 13,600 kg/m3
Patm = ρgh h = 0.760 m
Patm = (13,600 kg/m3
)(9.8 m/s2
)(0.760 m)
Patm = 101,300 PaPatm = 101,300 Pa

15. Absolute Pressure
Absolute Pressure:Absolute Pressure: The sum of the
pressure due to a fluid and the
pressure due to atmosphere.
Gauge Pressure:Gauge Pressure: The difference
between the absolute pressure and
the pressure due to the atmosphere:
Absolute Pressure = Gauge Pressure + 1 atmAbsolute Pressure = Gauge Pressure + 1 atm
h
∆P = 196 kPa
1 atm = 101.3 kPa
∆P = 196 kPa
1 atm = 101.3 kPa
Pabs = 196 kPa + 101.3 kPa
Pabs = 297 kPaPabs = 297 kPa

16. Pascal’s Law
Pascal’s Law: An external pressure applied to
an enclosed fluid is transmitted uniformly
throughout the volume of the liquid.
FoutFin AoutAin
Pressure in = Pressure outPressure in = Pressure out
in out
in out
F F
A A
=

17. Example 3. The smaller and larger pistons of a
hydraulic press have diameters of 4 cm and 12 cm.
What input force is required to lift a 4000 N weight
with the output piston?
Fout
Fin AouttAin
;in out out in
in
in out out
F F F A
F
A A A
= =
2
2
(4000 N)( )(2 cm)
(6 cm)
inF
π
π
=
2
;
2
D
R Area Rπ= =
F = 444 NF = 444 N
Rin= 2 cm; R = 6 cm

18. ABSOLUTE, GAGE, AND VACUUM
PRESSURES
 Actual pressure at a give point is called the
absolute pressure.
 Most pressure-measuring devices are calibrated
to read zero in the atmosphere, and therefore
indicate gage pressure, Pgage=Pabs - Patm.
 Pressure below atmospheric pressure are called
vacuum pressure, Pvac=Patm - Pabs.

19. Absolute, gage, and vacuum pressures

20. PRESSURE AT A POINT
 Pressure at any point in a fluid is the same in all
directions.
 Pressure has a magnitude, but not a specific
direction, and thus it is a scalar quantity.

21. SCUBA DIVING AND HYDROSTATIC
PRESSURE

22. PRESSURE MEASUREMENT
 Pressure is an important variable in fluid mechanics and
many instruments have been devised for its
measurement.
 Many devices are based on hydrostatics such as
barometers and manometers, i.e., determine pressure
through measurement of a column (or columns) of a
liquid using the pressure variation with elevation
equation for an incompressible fluid.

23. PRESSURE
 Force exerted on a unit
area : Measured in kPa
 Atmospheric pressure at
sea level is 1 atm, 76.0 mm
Hg, 101 kPa
 In outer space the
pressure is essentially
zero. The pressure in a
vacuum is called absolute
zero.
 All pressures referenced
with respect to this zero
pressure are termed
absolute pressures.

24.  Many pressure-
measuring devices
measure not absolute
pressure but only
difference in pressure.
This type of pressure
reading is called gage
pressure.
 Whenever atmospheric
pressure is used as a
reference, the possibility
exists that the pressure
thus measured can be
either positive or
negative.
 Negative gage pressure
are also termed as
vacuum pressures.

25. MANOMETERS
U Tube
Enlarged Leg
Two Fluid
Inclined Tube
Inverted U
Tube

26. THE MANOMETER
1 2
2 atm
P P
P P ghρ
=
= +
 An elevation change of
∆z in a fluid at rest
corresponds to ∆P/ρg.
 A device based on this is
called a manometer.
 A manometer consists of
a U-tube containing one
or more fluids such as
mercury, water, alcohol,
or oil.
 Heavy fluids such as
mercury are used if large
pressure differences are
anticipated.

27. MUTLIFLUID MANOMETER
 For multi-fluid systems
 Pressure change across a fluid
column of height h is ∆P = ρgh.
 Pressure increases downward, and
decreases upward.
 Two points at the same elevation in
a continuous fluid are at the same
pressure.
 Pressure can be determined by
adding and subtracting ρgh terms.
2 1 1 2 2 3 3 1P gh gh gh Pρ ρ ρ+ + + =

28. MEASURING PRESSURE DROPS
 Manometers are well--
suited to measure
pressure drops across
valves, pipes, heat
exchangers, etc.
 Relation for pressure
drop P1-P2 is obtained by
starting at point 1 and
adding or subtracting
ρgh terms until we reach
point 2.
 If fluid in pipe is a gas,
ρ2>>ρ1 and P1-P2= ρgh

29. THE BAROMETER
C atm
atm
P gh P
P gh
ρ
ρ
+ =
=
 Atmospheric pressure is
measured by a device called a
barometer; thus,
atmospheric pressure is often
referred to as the barometric
pressure.
 PC can be taken to be zero
since there is only Hg vapor
above point C, and it is very
low relative to Patm.
 Change in atmospheric
pressure due to elevation has
many effects: Cooking, nose
bleeds, engine performance,
aircraft performance.

30. Measuring pressure (1)
Manometers
h
p1
p2=pa
liquid
density ρ
x y
z
p1 = px
px = py
pz= p2 = pa
(negligible
pressure change
in a gas)
(since they are at
the same height)
py - pz = ρgh
p1 - pa = ρgh
So a manometer measures gauge pressure.

31. Measuring Pressure (2)
Barometers
A barometer is used to measure the
pressure of the atmosphere. The
simplest type of barometer consists of a
column of fluid.
p1 =
0
vacuum
h
p2 = pa
p2 - p1 = ρgh
pa = ρgh
examples
water: h = pa/ρg =105
/(103
*9.8) ~10m
mercury: h = pa/ρg =105
/(13.4*103
*9.8)
~800mm