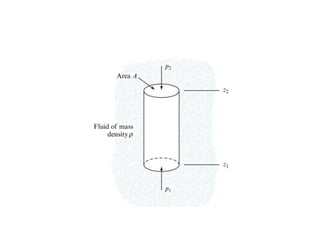
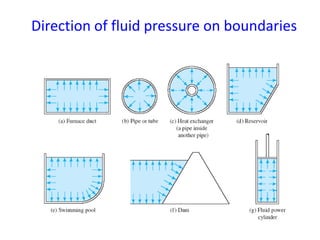
1. Fluid statics deals with fluids at rest, where only normal forces due to pressure are present, not shear stresses. 2. Pressure is defined as force per unit area and can be calculated using equations for either finite or infinite areas. 3. Pascal's principles state that pressure acts uniformly in all directions on an enclosed fluid and acts perpendicular to solid boundaries containing the fluid.

1. FLUID STATICS

2. Fluid Statics
• Fluid Statics means fluid at rest.
• At rest, there are no shear stresses, the only force is the
normal force due to pressure is present.
• Pressure is defined as:
• “Force per Unit Area” Or
“The amount of force exerted on a unit area of a substance
or on a surface.”
• This can be stated by the equation:
• Units : N/m2(Pa), lbs/ft2 (psf), lbs/in2 (psi)
Area)
Finite
(For
A
F
p 
Area)
Infinite
(For
dA
dF
p 

3. Example
A load of 200 pounds (lb) is exerted on a piston confining oil
in a circular cylinder with an inside diameter of 2.50 inches
(in). Compute the pressure in the oil at the piston.
Solution:

4. Principles about Pressure
• Two important principles about pressure were described by
Pascal, a seventeenth-century scientist:
1. Pressure acts uniformly in all directions on a small volume
of a fluid.
2. In a fluid confined by solid boundaries, pressure acts
perpendicular to the boundary.

5. Direction of fluid pressure on boundaries

6. Pressure at a Point is same in All direction
(Pascal’s Law)
x
x
x
z
x
p
p
Therefore;
cos
dl
dz
Since
0
dz
dy
p
-
dy
dl
cos
p
;
0
F
8.
Zero.
to
equal
be
must
direction
any
in
element
on
components
force
the
of
Sum
:
Condition
m
Equilibriu
7.
rest.
at
is
fluid
the
since
involved,
is
force
l
tangentia
No
6.
cancel.
they
because
considered
be
not
need
direction
y
in
Forces
5.
direction.
vertical
and
horizontal
in
pressure
avg.
are
p
and
p
4.
direction.
any
in
pressure
Avg.
p
Let
3.
paper).
of
plane
ular to
(perpendic
dy
Thickness
2.
rest.
at
fluid
of
element
shaped
wedge
a
Consider
1.










7. Pressure at a Point is same in All direction
direction.
all
in
same
is
rest
at
fluid
a
in
point
any
at
pressure
Thus
case.
l
dimensiona
three
a
g
considerin
by
py
p
proof
also
can
We
10.
p
p
Therefore;
sin
dl
dx
Since
order.
higher
to
due
term
3rd
Neglecting
0
dz
dy
dx
2
1
sin
dy
dl
p
-
dy
dx
p
;
0
F
9.
z
z
z











8. Variation of pressure vertically in a fluid
under gravity

11. Example

12. Pressure expressed in Height of Fluid
• The term elevation means the vertical distance from
some reference level to a point of interest and is
called z.
• A change in elevation between two points is called
h. Elevation will always be measured positively in
the upward direction.
• In other words, a higher point has a larger elevation
than a lower point.
• Fig shows the illustration of reference level for
elevation.

13. Relationship between Pressure and Elevation:

14. Pressure Head
• It is the pressure expressed in terms of height of fluid.
• h=p/ represents the energy per unit wt. stored in the fluid
by virtue of pressure under which the fluid exists. This is also
called the elevation head or potential head.

p
h 

16. Example
An open tank contains water 1.40m deep covered by a 2m
thick layer of oil (s=0.855). What is the pressure head at the
bottom of the tank, in terms of a water column?

17. m
p
h
h
h
p
SOLUTION
m
h
m
p
m
kN
x
h
m
kN
x
m
kN
w
b
we
w
w
o
o
b
w
w
i
o
o
o
w
11
.
3
81
.
9
51
.
30
30.51kN/m
9.81(1.4)
(8.39)2
2
11
.
3
710
.
1
40
.
1
h
h
So
710
.
1
81
.
9
78
.
16
h
:
oil
of
equivalent
for water
/
78
.
16
2
39
.
8
p
:
interface
For
/
39
.
8
81
.
9
855
.
0
/
81
.
9
2
oe
we
oe
2
i
3
3






























Solution: