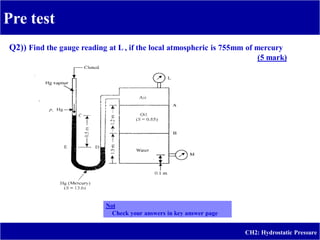
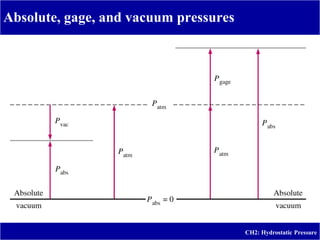
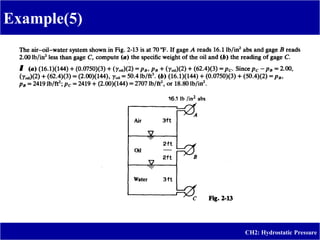
This document provides an overview and instruction on hydrostatic pressure for students, including defining hydrostatic pressure, discussing pressure measurement devices like manometers, calculating pressure at various points, and providing examples of solving hydrostatic pressure problems. The goal is for students to understand how pressure varies with depth in fluids, be able to use equations to calculate pressure, and describe common pressure measurement tools including piezometers, U-tube manometers, and inclined tube manometers. Practice problems are provided to help students apply the concepts.