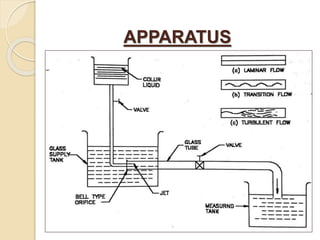
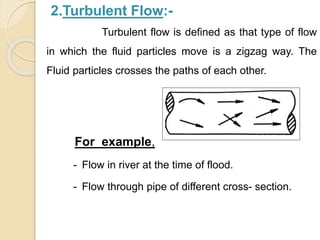
- The document summarizes Reynolds' experiment from 1883 that demonstrated laminar and turbulent fluid flow. - Laminar flow occurs at low velocities and has fluid particles moving in straight, parallel paths. Turbulent flow occurs at higher velocities and has fluid particles moving in a zigzag pattern, crossing each other's paths. - The Reynolds number is used to characterize the transition between laminar and turbulent flow, depending on whether it is less than, greater than, or between 2000-4000. - Examples are provided to calculate the Reynolds number and classify flow type in different pipe flow scenarios based on viscosity, velocity, diameter, and other properties.

1. SHREE SA’D VIDYA MANDAL
INSTITUTE OF TECHNOLOGY
DEPARTMENT OF CIVIL
ENGINEERING

2. Subject:-
Fluid
Mechanics
Topic:-Reynolds experiment

3. -:PRESENTED BY:-
Name
 Arvindsai
 Dhaval
 Fahim Patel
 Navazhushen Patel
 M.Asfak Patel
Enrollment no.
130454106002
130454106001
140453106005
140453106008
140453106007

4. INTRODUCTION
Prof. Osborne Reynolds conducted the
experiment in the year 1883.
This was conducted to demonstrate the
existence of two types of flow :-
1.Laminar Flow
2.Turbulent Flow

5. 1.Laminar Flow:-
Laminar flow is defined as that type of flow
in which the fluid particles move along well-defined
paths or stream lines and all the stream lines are
straight and parallel.
Factors responsible for laminar flow are:-
- High viscosity of fluid.
- Low velocity of flow.
- Less flow area.
For example,
‐ Flow through pipe of uniform cross-section.

6. 2.Turbulent Flow:-
Turbulent flow is defined as that type of flow
in which the fluid particles move is a zigzag way. The
Fluid particles crosses the paths of each other.
For example,
- Flow in river at the time of flood.
- Flow through pipe of different cross- section.

7. What is Reynolds Number ?
 The ratio of inertia force to viscous force
is said to be the Reynolds number (RN).

8. APPARATUS

9. Observation by Reynolds
1. At low velocity, the
dye will move in a
line parallel to the
tube and also it
does not get
dispersed.
2. At velocity little
more than before
the dye moves in a
wave form.
3. At more velocity the
dye will no longer
move in a straight-

10. FORMULAS
Where,
ρ =density of liquid (Kg/m3 )
V=mean velocity of liquid
m/S
D=diameter of pipe(m)
µ=dynamic velocity(N.S/m2
)
=kinematic viscosity(m2
/S)
Where
Reynold number is a dimensionless quantity.
ν
VxD
R
μ
ρxVxD
R
ForceViscous
ForceInertia
R
N
N
N








11. Types Of Flows Based On Reynold
Number:-
 If Reynold number, RN < 2000 the flow is
laminar flow.
 If Reynold number, RN > 4000 the flow is
turbulent flow.

12.  If Reynold number i.e. 2000 < RN < 4000,we
observe a flow in which we can see both
laminar and turbulent flow to gather. This flow is
called Transition flow.
 RN = 2300 is usually accepted as the value at
transition , RN that exists anywhere in the
transition region is called the critical Reynolds
number.

14. EXAMPLE

15. Example 1 :- An oil of viscosity 0.5 stoke is
flowing through a pipe of 30 cm in diameter at a
rate of 320 liters per second. Find the head loss
due to friction for the pipe length of 60 cm.
Solution:-
Q=320 liters/second
=0.32 m3/s
d=30 cm=0.30 m x 0.302
=0.070m2
L=60 m
=0.5 stoke
= 0.5 x 10-4 m2/s V= Q/A=0.32/0.0707
=4.52 m/s

16.  Reynolds number(RN):-
/sm10x6.156
RN1/4
0.079
f
Turbulent.isFlow4000)(27,120
4)-10x(0.5
0.30)x(4.52
ν
VxD
R
μ
ρxVxD
R
24-
N
N







17. • Head loss due to Friction:-
m5.128
0.30x9.81x2
(4.52)x60x10x6.156x4
2.g.d
4.f.l.V
hf
23-
2




18.  Example 2:- An oil of viscosity 0.9 and viscosity
0.06 poise is flowing through a pipe of diameter
200 mm at the rate of 60 liters per second. Find
the head loss due to friction for a 500 m length
of pipe. find the power required to maintain this
flow
Solution:-
Q = 60 liters/second x 0.202 = 0.0314
m2
= 0.06 m3/s
d = 200 cm ρ = 0.9 x1000 =
900kg/m3
= 0.20 m

19.  Reynolds number(RN):-
0.0051
1/4(0.079)/RNf
m/s1.91
Q/AV
TurbulentisFlow4000)(57,300
(0.006
0.20x1.91x900







20.  Head loss due to Friction:-
• Power required:-
kW5.02P
1000
9.48x0.06x9.81x900
μ
hfxQxxP
P
waterofm9.48
02x9.81x0.2
(1.91x30x0.0051x4
2.g.d
4.f.l.V
hf
g
)2
2







21.  Example 3:- oil of Sp. Gr 0.095 is flowing
through a pipe of 20 cm in diameter. if a rate of
flow 50 liters/second and viscosity of oil is 1
poise , decide the type of flow.
Solution:-
Q = 50 liters/second x 0.202 =0.314 m2
= 0.05m3/s
D =20 cm = 0.20 m ρ=0.95 x 1000 =950 kg/m3
µ = 1.0poise
= 0.1 Ns/m3 V= Q/A=0.05/0.0314
=1.59m/s

22.  Reynolds number(RN):-
.TransitionisFlow4000)Rn(20003021
0.1
0.20x1.59x950
μ
DxVxρ
RN
..



23.  Example 4:- Liquid is flowing through a pipe of
200 mm in diameter. Tube with mean viscosity
of oil 2 m/sec. If density of liquid is 912 kg/ m3
and viscosity is 0.38 N.S/m2 the type of flow.
Solution:-
V= 2 m/sec
d= 20 cm=0.20 m x
0.202=0.314m2
µ = 0.38 Ns/m3
ρ =950 kg/m3

24.  Reynolds number(RN):-
Laminar.isFlow(2000)960
0.38
0.20x2x912
μ
DxVxρ
RN


