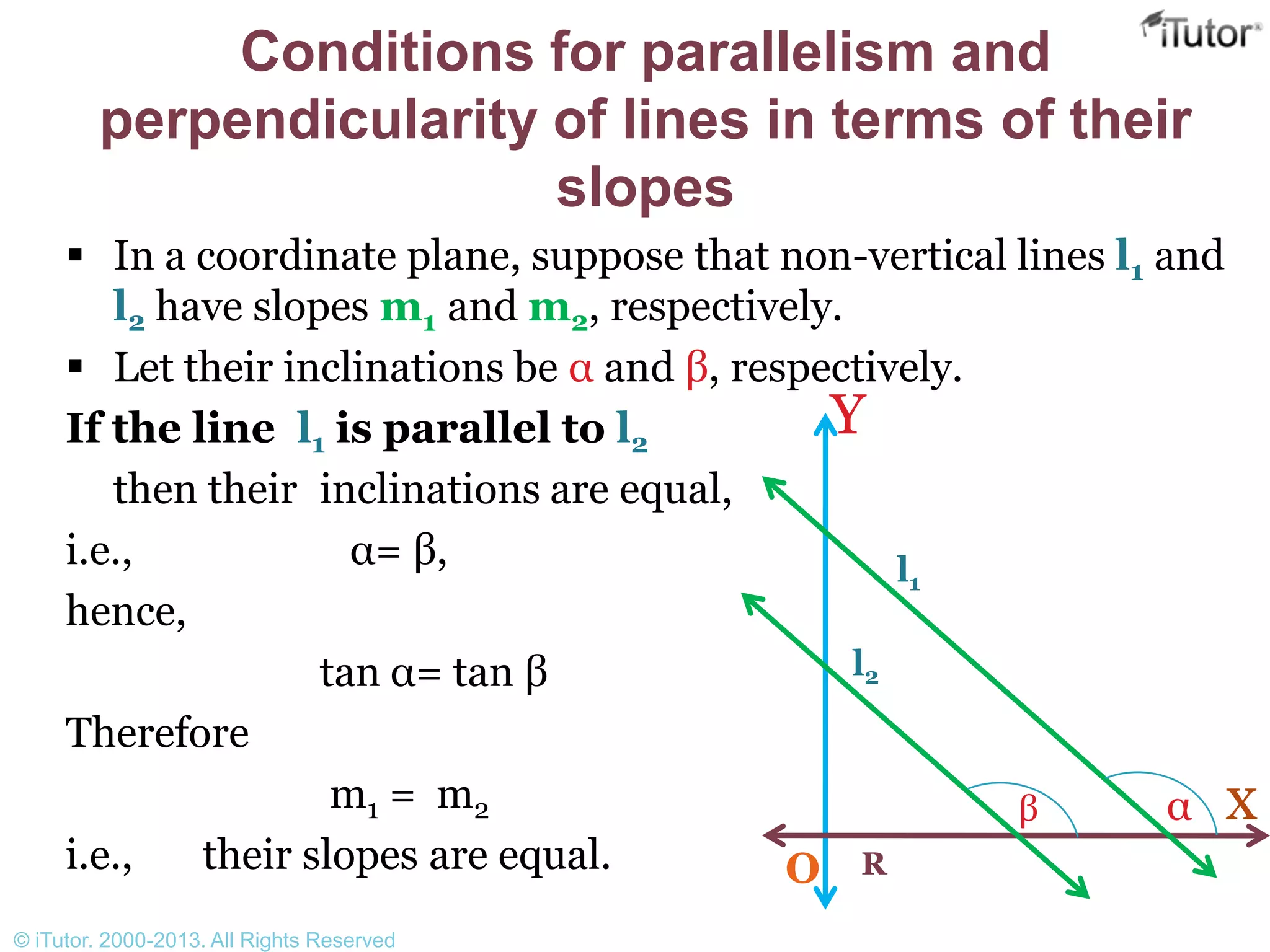
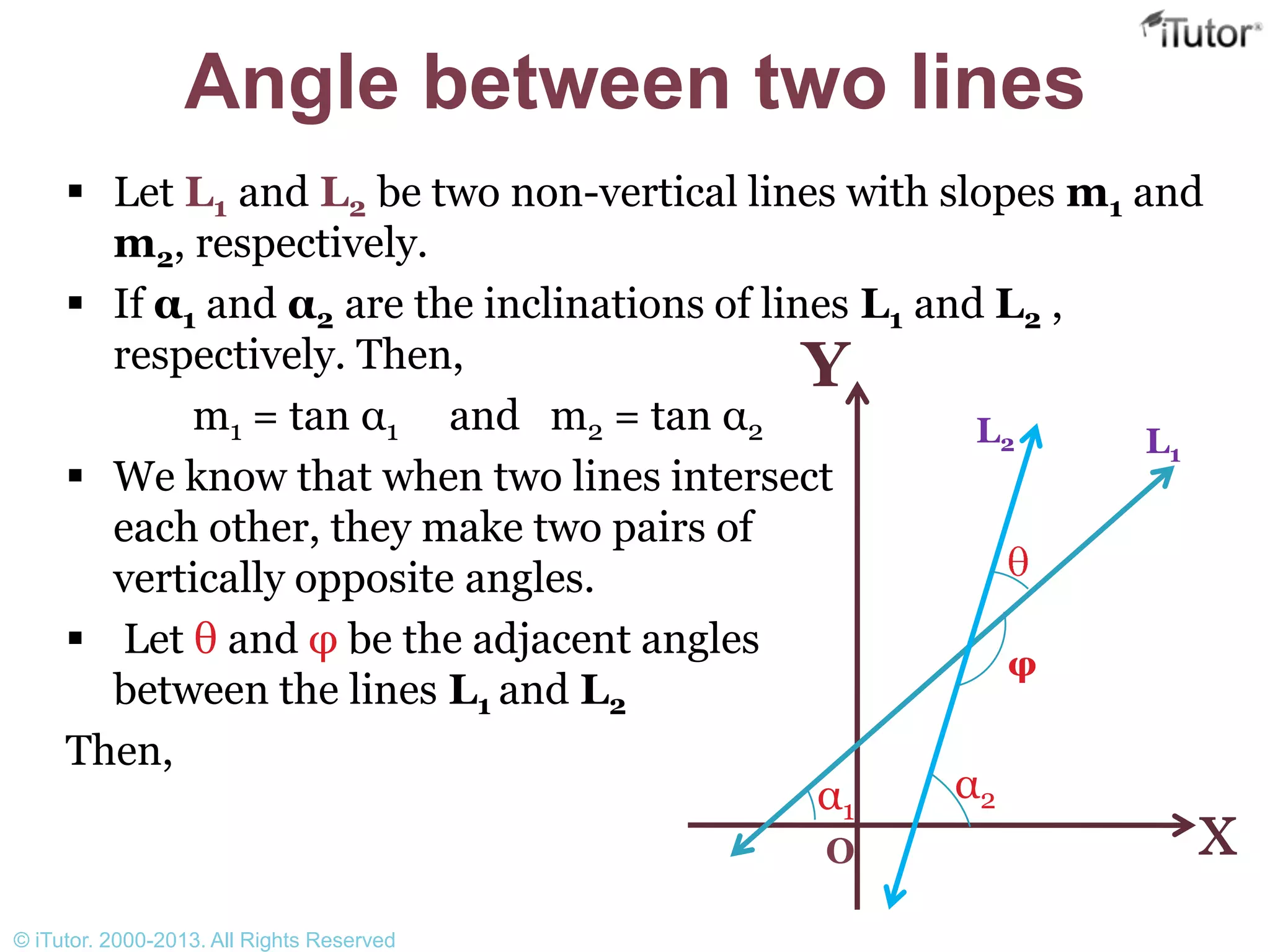
This document discusses slope and how to calculate it from the coordinates of two points on a line. It defines slope as the tangent of the angle of inclination of the line with respect to the x-axis. It provides the formula for calculating slope given two points and discusses how to determine if two lines are parallel, perpendicular, or the angle between them based on their slopes.