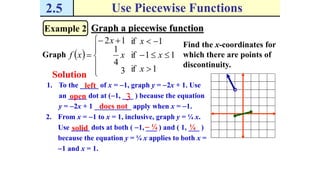
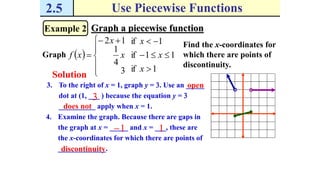
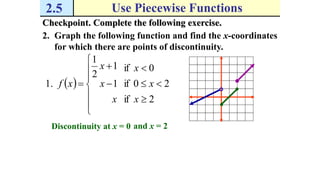
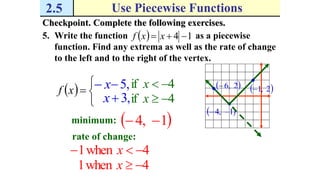
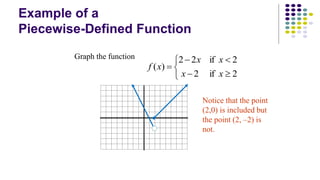
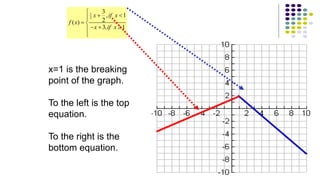
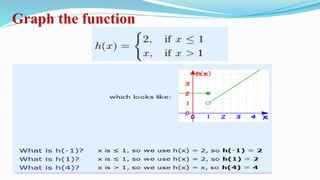
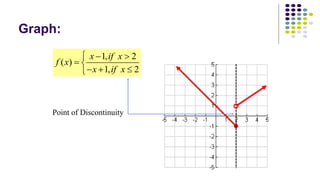
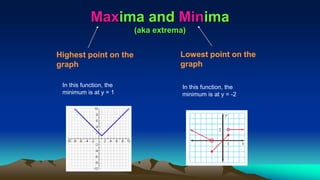
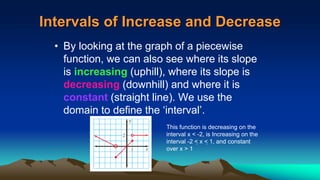
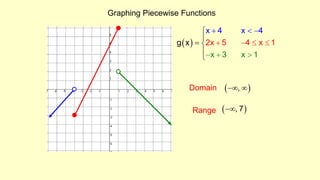
The document discusses piecewise functions, which are functions defined by multiple rules over different parts of the domain. It provides examples of piecewise functions, including how to graph them by applying each rule over the appropriate portion of the domain. It also discusses evaluating piecewise functions at given values, writing piecewise functions based on graphs, and analyzing properties like extrema. Piecewise functions allow modeling of real-world situations using multiple equations each corresponding to a part of the input range.

1. Piecewise
Functions

2. 2
Piecewise-Defined Functions
 Notice that this function is defined by different rules for
different parts of its domain. Functions whose definitions
involve more than one rule are called piecewise-defined
functions.
 Graphing one of these functions involves graphing each
rule over the appropriate portion of the domain.

3. Example of a
Piecewise-Defined Function






2if2
2if22
)(
xx
xx
xf
Graph the function
Notice that the point
(2,0) is included but
the point (2, –2) is
not.

4.  Up to now, we’ve been looking at
functions represented by a single
equation.
 In real life, however, functions are
represented by a combination of
equations, each corresponding to
a part of the domain.
 These are called piecewise
functions.

5. Piecewise Functions

6.  






1,13
1,12
xifx
xifx
xf
•One equation gives the value of f(x) when x ≤ 1
•And the other when x>1

7. Evaluate f(x) when x=0, x=2, x=4






2,12
2,2
)(
xifx
xifx
xf
•First you have to figure out which equation to use
•You NEVER use both
X=0
This one fits Into the top
equation
So:
0+2=2
f(0)=2
X=2
This one fits here
So:
2(2) + 1 = 5
f(2) = 5
X=4
This one fits here
So:
2(4) + 1 = 9
f(4) = 9

8. Graph:






1,3
1,
)( 2
3
2
1
xifx
xifx
xf
•For all x’s < 1, use the top graph (to the left of 1)
•For all x’s ≥ 1, use the bottom graph (to the
•right of 1)

9. Graphing a Piecewise Function

10. 1
2
3
, 1
2( )
3, 1
x if x
f x
x if x

 
 
  

x=1 is the breaking
point of the graph.
To the left is the top
equation.
To the right is the
bottom equation.

11. Graph the function

12. Graph:
1, 2
( )
1, 2
x if x
f x
x if x
  
 
  
Point of Discontinuity

14. Maxima and Minima
(aka extrema)
In this function, the
minimum is at y = 1
In this function, the
minimum is at y = -2
Highest point on the
graph
Lowest point on the
graph

15. Intervals of Increase and Decrease
• By looking at the graph of a piecewise
function, we can also see where its slope
is increasing (uphill), where its slope is
decreasing (downhill) and where it is
constant (straight line). We use the
domain to define the ‘interval’.
This function is decreasing on the
interval x < -2, is Increasing on the
interval -2 < x < 1, and constant
over x > 1

16. Piecewise Function – A function defined in pieces.
 
3
f
x 4 x 0
x 3 x 0
x
2

 
 


 f 3   2 3 3 3   
 f 6   3 6 14 4 
 f 5   3 5 14 1 
 f 2   2 2 3 1   
 f 0   2 0 33 
 
2
x x 3
x
x 1 x 2
xx 4 3 2f   










 f 0  0 44 
 f 5   
2
25 5 
 f 4  4 31 
 f 3 
 f 3 
 f 4 
3 21 
3 4 1  
 
2
14 6 

17.  
2x 5 x 1
g x x 3 1 x 3
3x 1 x 3
  

    
  
 g 6 
 g 2 
 g 0 
 g 1 
 g 3 
 3 6 11 7 
 2 1 5 7   
0 33  
2 13  
 2 3 5 11   
 
4 x 3
h x 2x 3 3 x 4
4x 7 x 6
 

    
  
 h 4 
 h 3 
 h 3 
 h 4 
 h 5 
 h 6 
4
4
 2 3 3 9 
 2 4 3 11 
DNE
 4 6 7 17 

18. Piecewise Function – Domain and Range
Domain
Range
(-6, 7)
(-1,5)
Domain
Range
[-7, 7]
(- 4.5,-1] ∪ [0, 4)

19. Domain
Range
(-7, -1)∪ (-1, 7]
[-1, 5) ∪ {6}
Domain
Range
(-7, 4) ∪ [5, 7)
[-7, -5) ∪ (-2, 7)

20. Graphing Piecewise Functions
 
x 4 x 4
2x
x 3 x
1
1
g x 5 4 x  
  
   
 




Domain  , 
Range  , 7

21.  
3 7 x 4
1
x 2 4 x 0
2
1
x 4
x
0 x 5
5 x 7
g

 
 
  



 

  
  




Domain
Range
(-7, 7]
(-4, -2) ∪ [-1, 4]

22.  
1
x 6 x 3
3
x 1 3 x 0h x
x 4 0 x 3
x 3 3 x 7

    
     
   

   
Domain
Range
[-6, 7]
[-4, 2] ∪ (4, 7)

23. • How do graph
piecewise
functions?

24. 2.5 Use Piecewise Functions
Example 1 Evaluate a piecewise function
Evaluate the function when x = 3.
 






2if,14
2if,1
xx
xx
xg
Solution
Because ______, use
_______ equation.
23 
second  _______xg 14 x
Substitute ___ for x.3  _________ g 3   134 
Simplify.____ 11

25. 2.5 Use Piecewise Functions
Checkpoint. Evaluate the function when x = 4 and x = 2.
 







0if,1
4
1
0if,23
1.
xx
xx
xf
04 
 4f   243  14
02 
 2f   12
4
1

2
3


26. 2.5 Use Piecewise Functions
Example 2 Graph a piecewise function
Graph  
1if
11if
1if
3
4
1
12







 

x
x
x
x
x
xf
Solution
Find the x-coordinates for
which there are points of
discontinuity.
1. To the _____ of x = 1, graph y = 2x + 1. Use
an _____ dot at (1, ___ ) because the equation
y = 2x + 1 __________ apply when x = 1.
left
3open
does not
2. From x = 1 to x = 1, inclusive, graph y = ¼ x.
Use _____ dots at both ( 1, ___ ) and ( 1, ___ )
because the equation y = ¼ x applies to both x =
1 and x = 1.
solid  ¼ ¼

27. 2.5 Use Piecewise Functions
Example 2 Graph a piecewise function
Graph  
1if
11if
1if
3
4
1
12







 

x
x
x
x
x
xf
Solution
Find the x-coordinates for
which there are points of
discontinuity.
3. To the right of x = 1, graph y = 3. Use an _____
dot at (1, ___ ) because the equation y = 3
__________ apply when x = 1.
3
open
does not
4. Examine the graph. Because there are gaps in
the graph at x = _____ and x = ___, these are
the x-coordinates for which there are points of
_____________.
1 1
discontinuity

28. 2.5 Use Piecewise Functions
Checkpoint. Complete the following exercise.
 
2if
20if
0if
1
1
2
1
1.













x
x
x
x
x
x
xf
2. Graph the following function and find the x-coordinates
for which there are points of discontinuity.
Discontinuity at x = 0 and x = 2

29. 2.5 Use Piecewise Functions
Example 3 Write a piecewise function
Write a piecewise function for the step
function shown. Describe any intervals over
which the function is constant.
For x between ___ and ___, including x = 1,
the graph is the line segment given by y = 1.
1 2
 





xf
,1 21if  x
For x between ___ and ___, including x = 2,
the graph is the line segment given by y = 2.
2 3
,2 32if  x
For x between ___ and ___, including x = 3,
the graph is the line segment given by y = 3.
3 4
,3 43if  x
So, a _____________
_________ for the
graph is as follows:
piecewise
function
The intervals over which the function
is ___________ are ____________,
____________, ______________.
constant 21  x
32  x 43  x

30. 2.5 Use Piecewise Functions
Example 4 Write and analyze a piecewise function
Write the function as a piecewise function.
Find any extrema as well as the rate of change of the function to
the left and to the right of the vertex.
  213  xxf
1. Graph the function. Find and label the vertex,
one point to the left of the vertex, and one point
to the right of the vertex. The graph shows one
minimum value of ____, located at the vertex,
and no maximum.  2,1 
2
2 4,3
 7,2
2

31. 2.5 Use Piecewise Functions
Example 4 Write and analyze a piecewise function
Write the function as a piecewise function.
Find any extrema as well as the rate of change of the function to
the left and to the right of the vertex.
  213  xxf
2. Find linear equations that represent each piece
of the graph.
 2,1 
2
2 4,3
 7,2
Left of vertex:
____m
 24 
 13 
3
  ___3__  xy 4 3
_____  xy 3 5
xy 34  9

32. 2.5 Use Piecewise Functions
Example 4 Write and analyze a piecewise function
Write the function as a piecewise function.
Find any extrema as well as the rate of change of the function to
the left and to the right of the vertex.
  213  xxf
2. Find linear equations that represent each piece
of the graph.
 2,1 
2
2 4,3
 7,2
Right of vertex:
____m
 27 
 12 
3
 __3__  xy 7 2
____  xy 3 1
xy 37  6

33. 2.5 Use Piecewise Functions
Example 4 Write and analyze a piecewise function
Write the function as a piecewise function.
Find any extrema as well as the rate of change of the function to
the left and to the right of the vertex.
  213  xxf
So the function may be written as
 2,1 
2
2 4,3
 7,2
 
1if
1if
,13
,53








x
x
x
x
xf
The extrema is a ____________ located at the
vertex ( 1, 2 ). The rate of change of the
function is ____ when x < 1 and ___ when x > 1.3
minimum
3

34. 2.5 Use Piecewise Functions
Checkpoint. Complete the following exercises.
4. Write a piecewise function for the step function shown.
Describe any intervals over which the function is
constant.
 





xf
,2 10if  x
,0 31if  x
,2 43if  x
Constant intervals:
10  x
31  x
43  x

35. 2.5 Use Piecewise Functions
Checkpoint. Complete the following exercises.
5. Write the function as a piecewise
function. Find any extrema as well as the rate of change
to the left and to the right of the vertex.
  14  xxf
 1,4 
 2,6  2,1 



xf
4if x,5x
4if x,3x
minimum:  1,4 
rate of change:
4when1  x
4when1 x