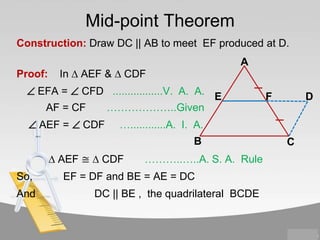
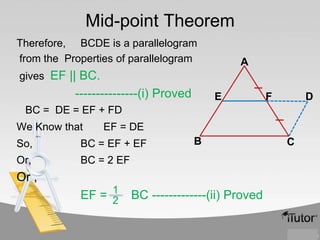
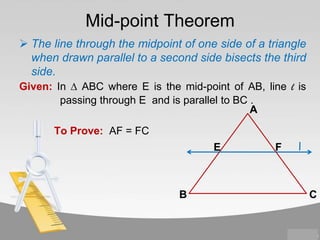
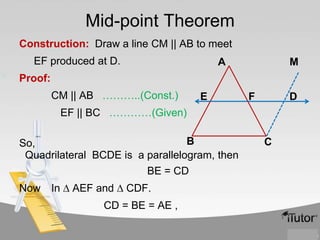
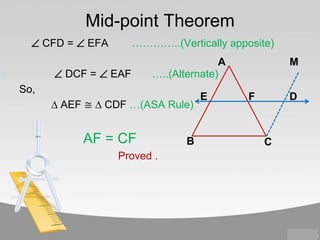
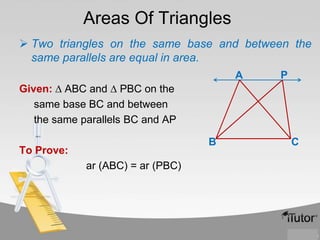
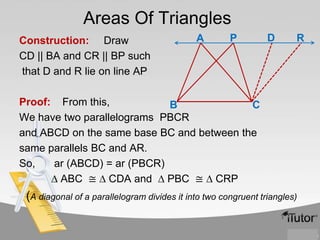
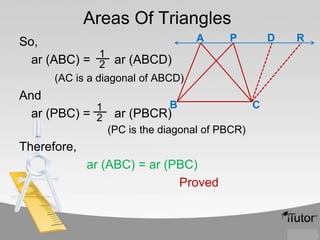
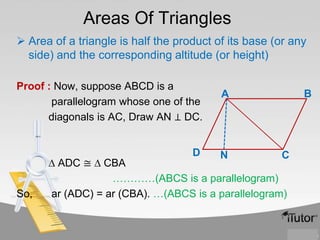
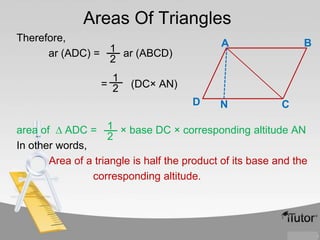
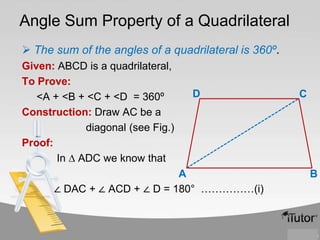
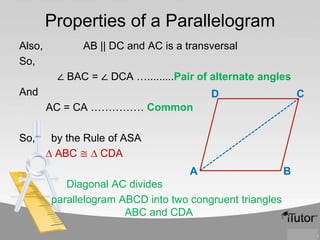
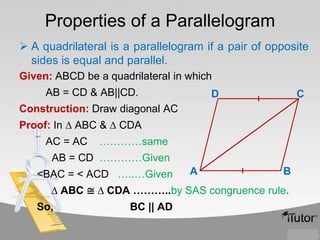
The document contains information about various properties of quadrilaterals, triangles, and parallelograms. It includes proofs of: 1) The sum of the interior angles of any quadrilateral is 360 degrees. 2) A diagonal of a parallelogram divides it into two congruent triangles. 3) If two triangles are on the same base and between the same parallels, they have equal areas.

1. By iTutor.com
T- 1-855-694-8886
Email- info@iTutor.com

2. Angle Sum Property of a Quadrilateral
 The sum of the angles of a quadrilateral is 360º.
Given: ABCD is a quadrilateral,
To Prove:
<A + <B + <C + <D = 360º
Construction: Draw AC be a
diagonal (see Fig.)
Proof:
In ∆ ADC we know that
D
A
∠ DAC + ∠ ACD + ∠ D = 180° ……………(i)
C
B

3. Angle Sum Property of a Quadrilateral
Similarly, in ∆ ABC,
∠ CAB + ∠ ACB + ∠ B = 180° …………. (ii)
Adding (i) and (ii), we get
∠ DAC + ∠ ACD + ∠ D +
D
∠ CAB + ∠ ACB + ∠ B
= 180° + 180° = 360°
Also, ∠ DAC + ∠ CAB =∠ A
and ∠ ACD + ∠ ACB = ∠ C
So,
i.e.,
C
A
B
∠ A + ∠ D + ∠ B + ∠ C = 360°
the sum of the angles of a quadrilateral is 360°.

4. Properties of a Parallelogram
 A diagonal of a parallelogram divides it into two
congruent triangles.
Given: ABCD be a parallelogram and AC be a diagonal
AC divides into two
D
C
triangles, ∆ ABC & ∆ CDA.
To prove: ∆ ABC ≅ ∆ CDA
Proof: In ∆ ABC and ∆ CDA
We know that BC || AD and
AC is a transversal
So,
A
∠ BCA = ∠ DAC ….(Pair of alternate angles)
B

5. Properties of a Parallelogram
Also,
So,
AB || DC and AC is a transversal
∠ BAC = ∠ DCA ….........Pair of alternate angles
And
D
C
AC = CA …………… Common
So,
by the Rule of ASA
∆ ABC ≅ ∆ CDA
A
Diagonal AC divides
parallelogram ABCD into two congruent triangles
ABC and CDA
B

6. Properties of a Parallelogram
 If each pair of opposite sides of a quadrilateral is
equal, then it is a parallelogram.
Given: Quadrilateral ABCD, sides AB and CD is equal and
also AD = BC
D
C
To Prove: ABCD is a Parallelogram
Construction: Draw diagonal AC
Proof: In ∆ ABC & ∆ CDA
∆ ABC ≅ ∆ CDA ……… S. S. S.
So,
∠ BAC = ∠ DCA
A
B
and
∠ BCA = ∠ DAC,
So that the line AB||DC and AD||BC ,
So that ABCD is a parallelogram

7. Properties of a Parallelogram
 If the diagonals of a quadrilateral bisect each other,
then it is a parallelogram.
Given: Quadrilateral ABCD, diagonal AC and BD
Where OA = OC and OB = OD D
C
To Prove: ABCD is a parallelogram
So,
∆ AOB ≅ ∆ COD
….….. SAS
Therefore,
O
∠ ABO = ∠ CDO
From this, we get AB || CD
Similarly,
A
BC || AD
Therefore ABCD is a parallelogram.
B

8. Properties of a Parallelogram
 A quadrilateral is a parallelogram if a pair of opposite
sides is equal and parallel.
Given: ABCD be a quadrilateral in which
AB = CD & AB||CD.
D
C
Construction: Draw diagonal AC
Proof: In ∆ ABC & ∆ CDA
AC = AC
…………same
AB = CD …………Given
<BAC = < ACD …..…Given
A
B
∆ ABC ≅ ∆ CDA ………..by SAS congruence rule.
So,
BC || AD

9. Properties of a Parallelogram
The opposite sides and opposite sides of a parallelogram are
respectively equal in measure.
b
c
3
Given:
Parallelogram abcd
4
1
a
2
To Prove: |ab| = |cd| and |ad| = |bc|
and abc = adc
d
Construction:
Draw the diagonal |ac|

10. Properties of a Parallelogram
The opposite sides and opposite sides of a parallelogram are
respectively equal in measure.
b
c
3
4
1
a
Proof: In the triangle abc and
the triangle adc
1 = 4 …….. Alternate angles
2 = 3 ……… Alternate angles
2
d
|ac| = |ac| …… Common
The triangle abc is congruent to the triangle adc

………ASA
|ab| = |cd| and |ad| = |bc|
and abc = adc
= ASA.

11. Mid-point Theorem
 The line which joins the midpoints of two sides of a
triangle is parallel to the third side and is equal to half
of the length of the third side
Given: In ∆ ABC where E and F are
mid-points of AB and AC respectively
To Prove:
(i) EF || BC
A
E
(ii) EF = 1 BC
2
B
F
C

12. Mid-point Theorem
Construction: Draw DC || AB to meet EF produced at D.
A
Proof:
In ∆ AEF & ∆ CDF
EFA =  CFD .................V. A. A.
………………..Given
AF = CF
AEF = CDF
E
∆ AEF ≅ ∆ CDF
And
D
…............A. I. A.
B
So,
F
………..…..A. S. A. Rule
EF = DF and BE = AE = DC
DC || BE , the quadrilateral BCDE
C

13. Mid-point Theorem
Therefore, BCDE is a parallelogram
from the Properties of parallelogram
A
gives EF || BC.
---------------(i) Proved
E
F
D
BC = DE = EF + FD
We Know that
EF = DE
So,
BC = EF + EF
Or,
B
BC = 2 EF
Or ,
EF = 1
2
BC -------------(ii) Proved
C

14. Mid-point Theorem
 The line through the midpoint of one side of a triangle
when drawn parallel to a second side bisects the third
side.
Given: In ∆ ABC where E is the mid-point of AB, line l is
passing through E and is parallel to BC .
A
To Prove: AF = FC
E
B
F
l
C

15. Mid-point Theorem
Construction: Draw a line CM || AB to meet
EF produced at D.
A
M
Proof:
CM || AB ………..(Const.)
E
F
D
EF || BC …………(Given)
B
So,
Quadrilateral BCDE is a parallelogram, then
BE = CD
Now
In ∆ AEF and ∆ CDF.
CD = BE = AE ,
C

16. Mid-point Theorem
 CFD =  EFA
…………..(Vertically apposite)
 DCF =  EAF
A
…..(Alternate)
So,
∆ AEF ≅ ∆ CDF …(ASA Rule)
AF = CF
Proved .
B
E
M
F
D
C

17. Areas Of Parallelograms
 Parallelograms on the same base and between the
same parallels are equal in area.
Given: Two parallelograms ABCD and EFCD,
A
E
On the same base DC and
between the same parallels
AF and DC
To Prove:
D
ar (ABCD) = ar (EFCD)
B
C
F

18. Areas Of Parallelograms
Proof: In ∆ ADE and ∆ BCF,
AD || BC
∠ DAE = ∠ CBF
………..
(Corresponding angles)
A
ED || FC
∠ AED = ∠ BFC
E
B
(Corresponding angles)
Therefore,
∠ ADE = ∠ BCF
D
C
(Angle sum property of a triangle)
Also,
So,
AD = BC (Opposite sides of the parallelogram ABCD)
∆ ADE ≅ ∆ BCF
………(By ASA rule)
F

19. Areas Of Parallelograms
Therefore,
ar (ADE) = ar (BCF) -------(Congruent figures have equal areas)
ar (ABCD) = ar (ADE) + ar (EDCB) A
E
B
F
= ar (BCF) + ar (EDCB)
= ar (EFCD)
So,
D
C
Parallelograms ABCD and EFCD are equal in area.

20. Areas Of Triangles
 Two triangles on the same base and between the
same parallels are equal in area.
A
P
Given: ∆ ABC and ∆ PBC on the
same base BC and between
the same parallels BC and AP
B
To Prove:
ar (ABC) = ar (PBC)
C

21. Areas Of Triangles
Construction: Draw
CD || BA and CR || BP such
that D and R lie on line AP
A
P
D
R
Proof: From this,
B
C
We have two parallelograms PBCR
and ABCD on the same base BC and between the
same parallels BC and AR.
So,
ar (ABCD) = ar (PBCR)
∆ ABC ≅ ∆ CDA and ∆ PBC ≅ ∆ CRP
(A diagonal of a parallelogram divides it into two congruent triangles)

22. Areas Of Triangles
So,
1
ar (ABC) = 2 ar (ABCD)
A
D
P
(AC is a diagonal of ABCD)
And
B
1
ar (PBC) = 2 ar (PBCR)
(PC is the diagonal of PBCR)
Therefore,
ar (ABC) = ar (PBC)
Proved
C
R

23. Areas Of Triangles
 Area of a triangle is half the product of its base (or any
side) and the corresponding altitude (or height)
Proof : Now, suppose ABCD is a
parallelogram whose one of the
diagonals is AC, Draw AN ⊥ DC.
D
So,
B
A
N
C
∆ ADC ≅ ∆ CBA
…………(ABCS is a parallelogram)
ar (ADC) = ar (CBA). …(ABCS is a parallelogram)

24. Areas Of Triangles
Therefore,
ar (ADC) = 1 ar (ABCD)
2
1
= 2
B
A
(DC× AN)
D
N
C
area of ∆ ADC = 1 × base DC × corresponding altitude AN
2
In other words,
Area of a triangle is half the product of its base and the
corresponding altitude.

25. Call us for more
Information:
1-855-694-8886
Visit
www.iTutor.com
The End