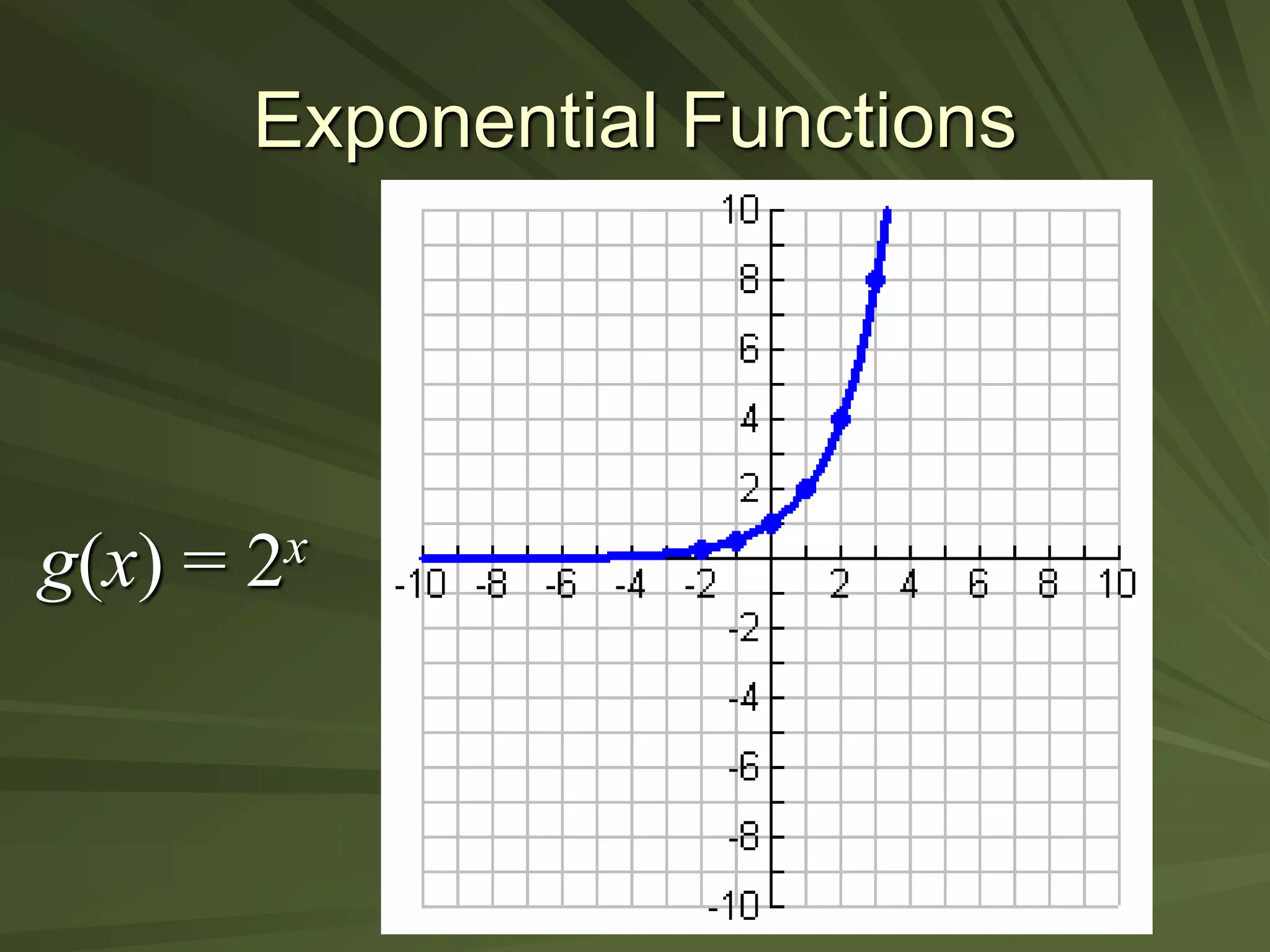
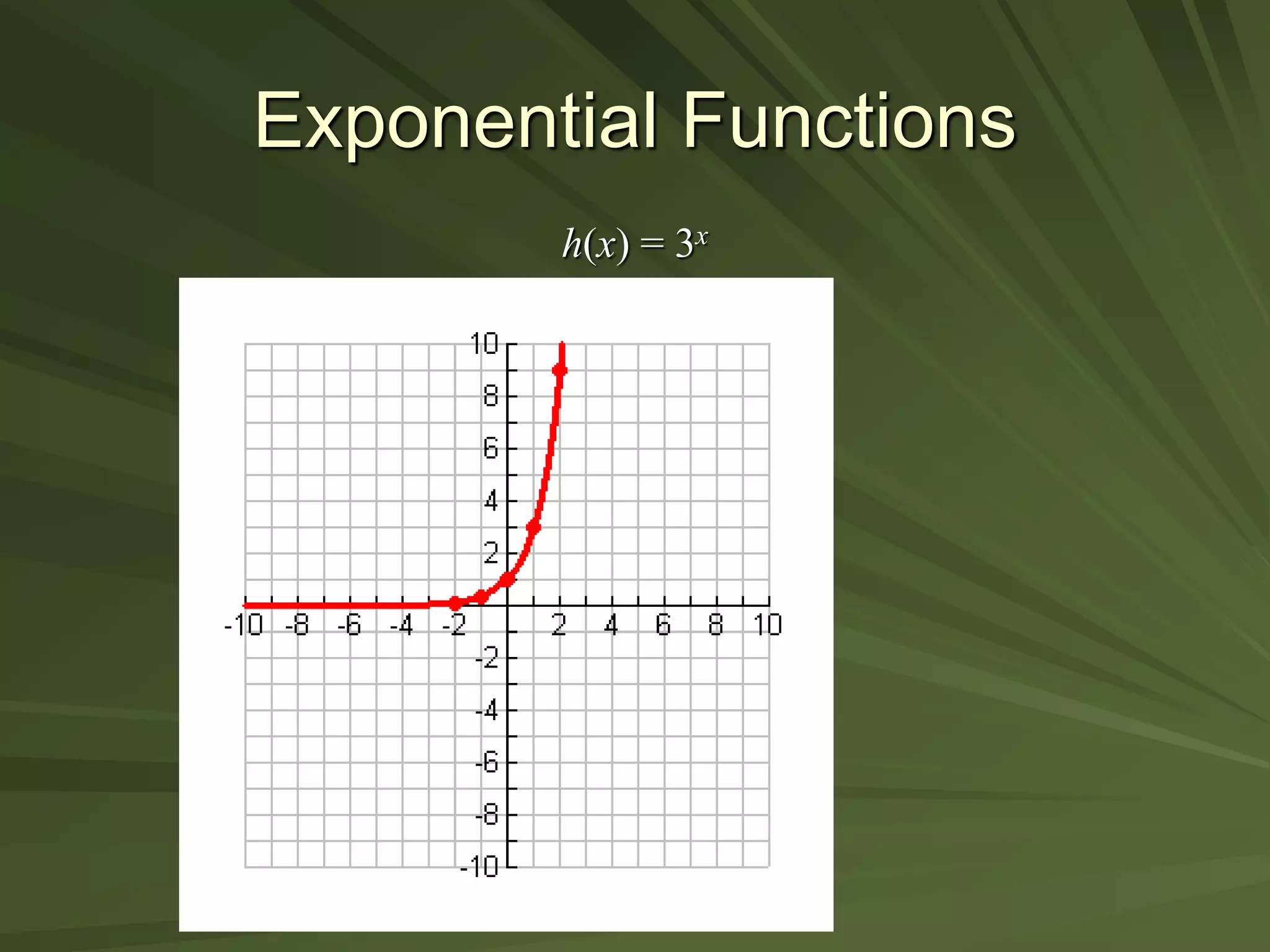
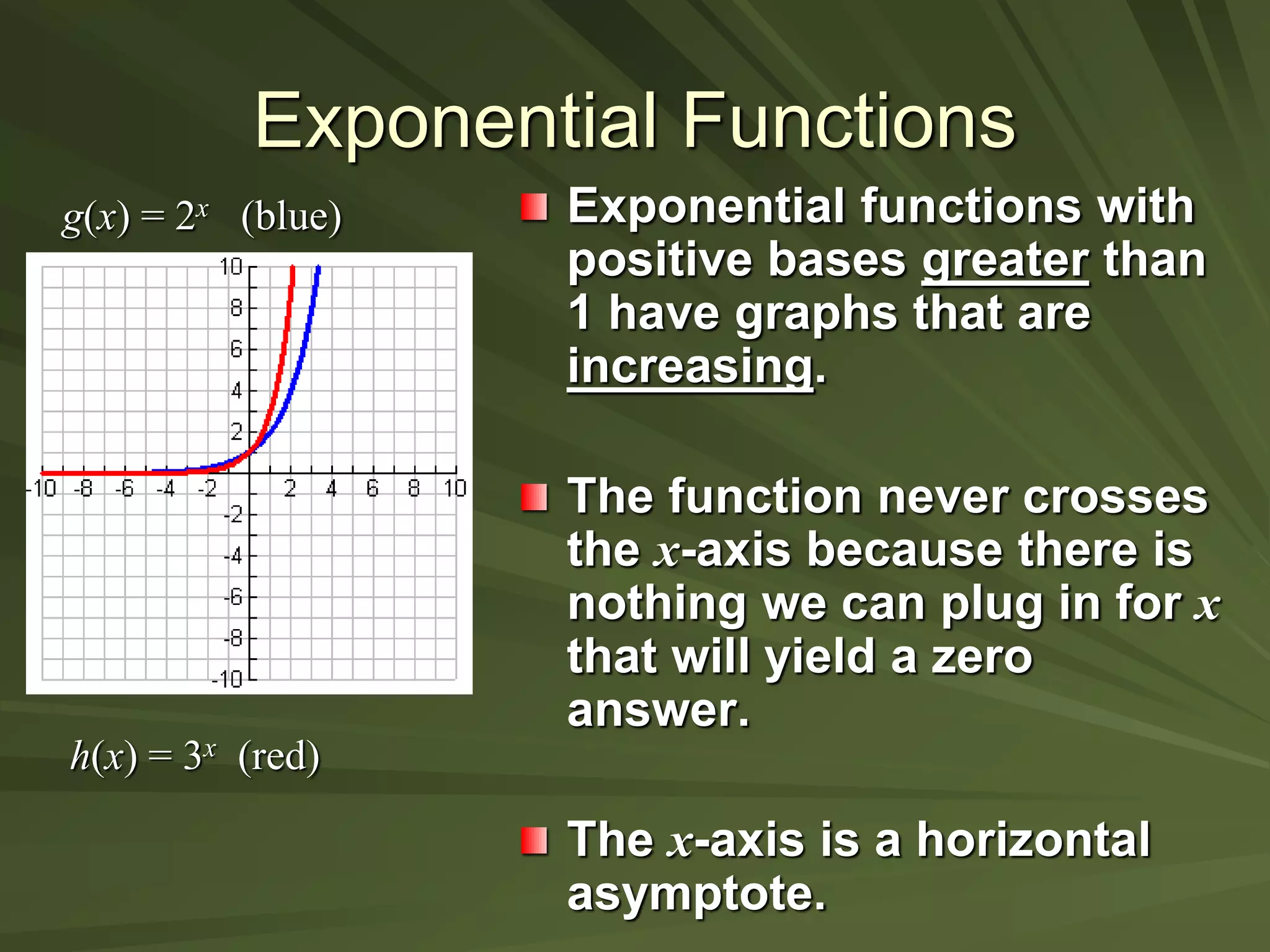
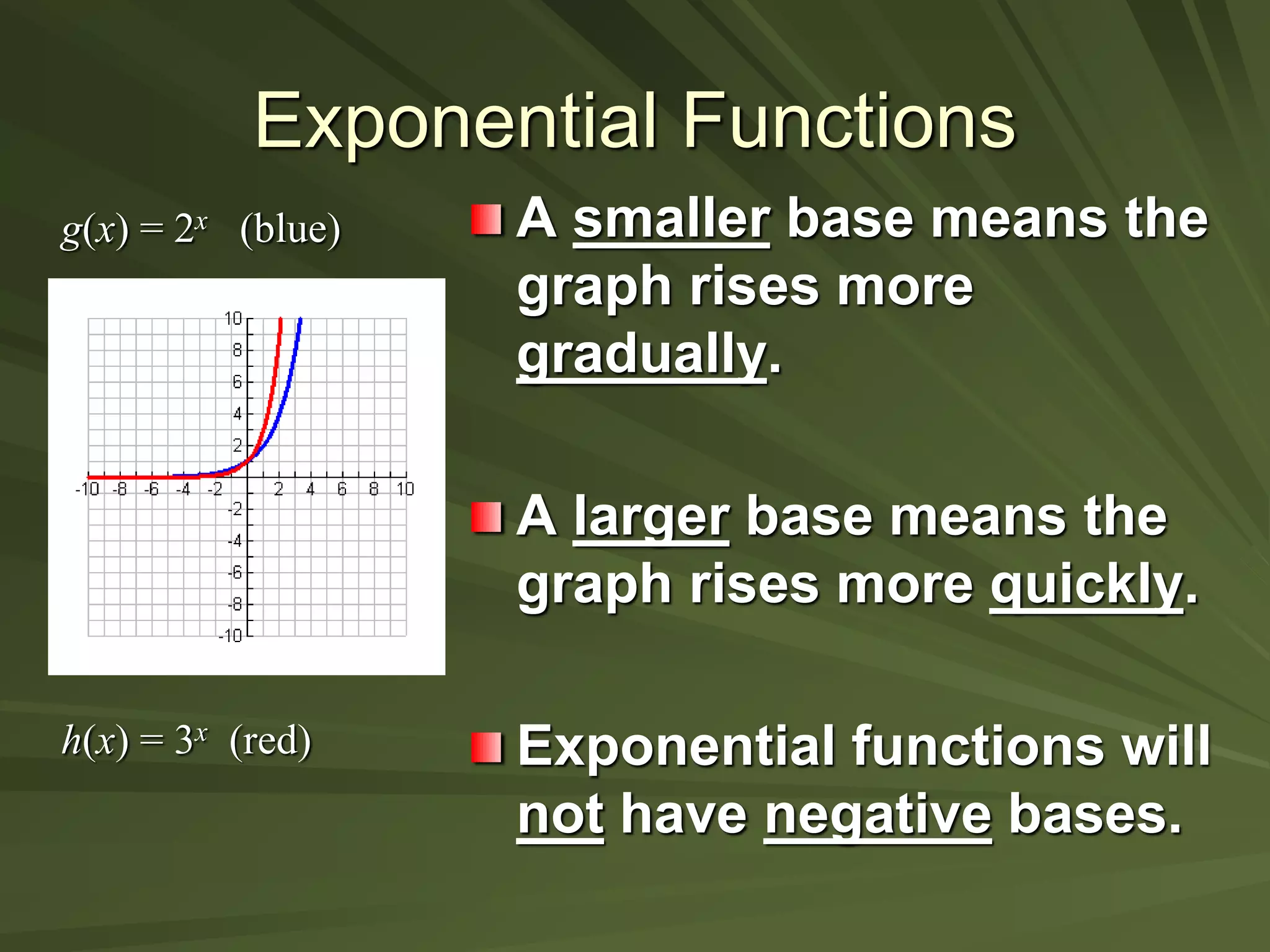
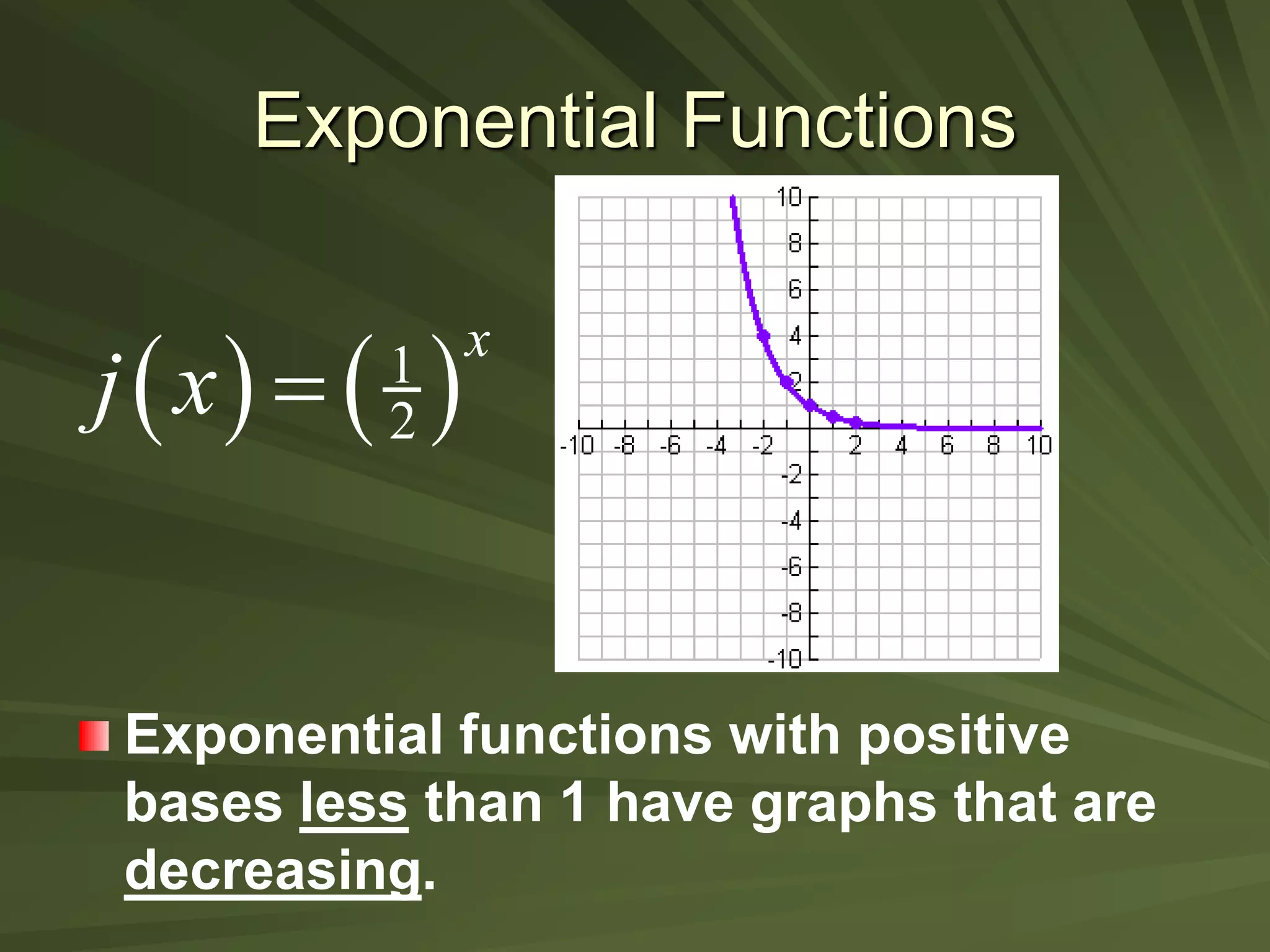
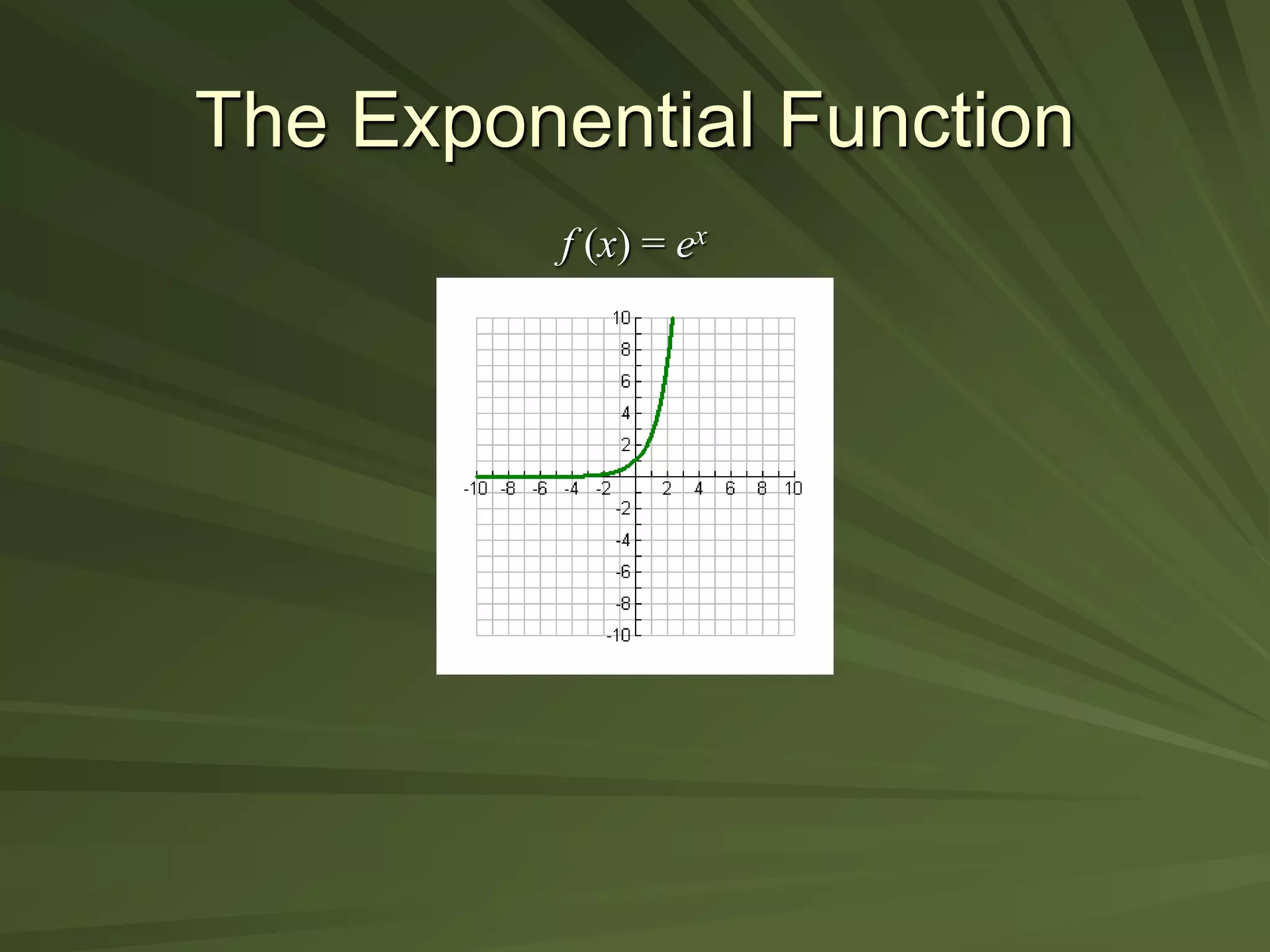
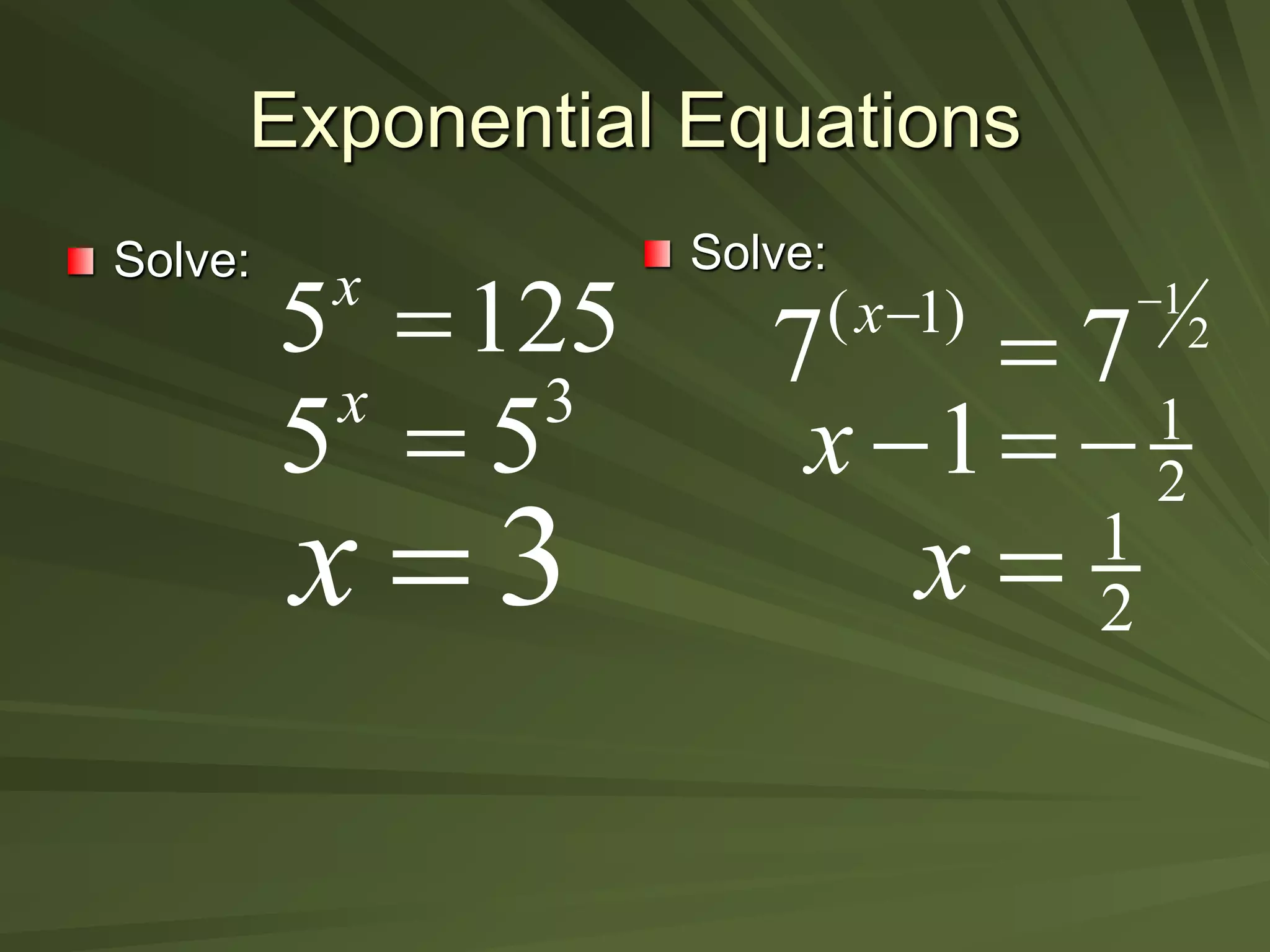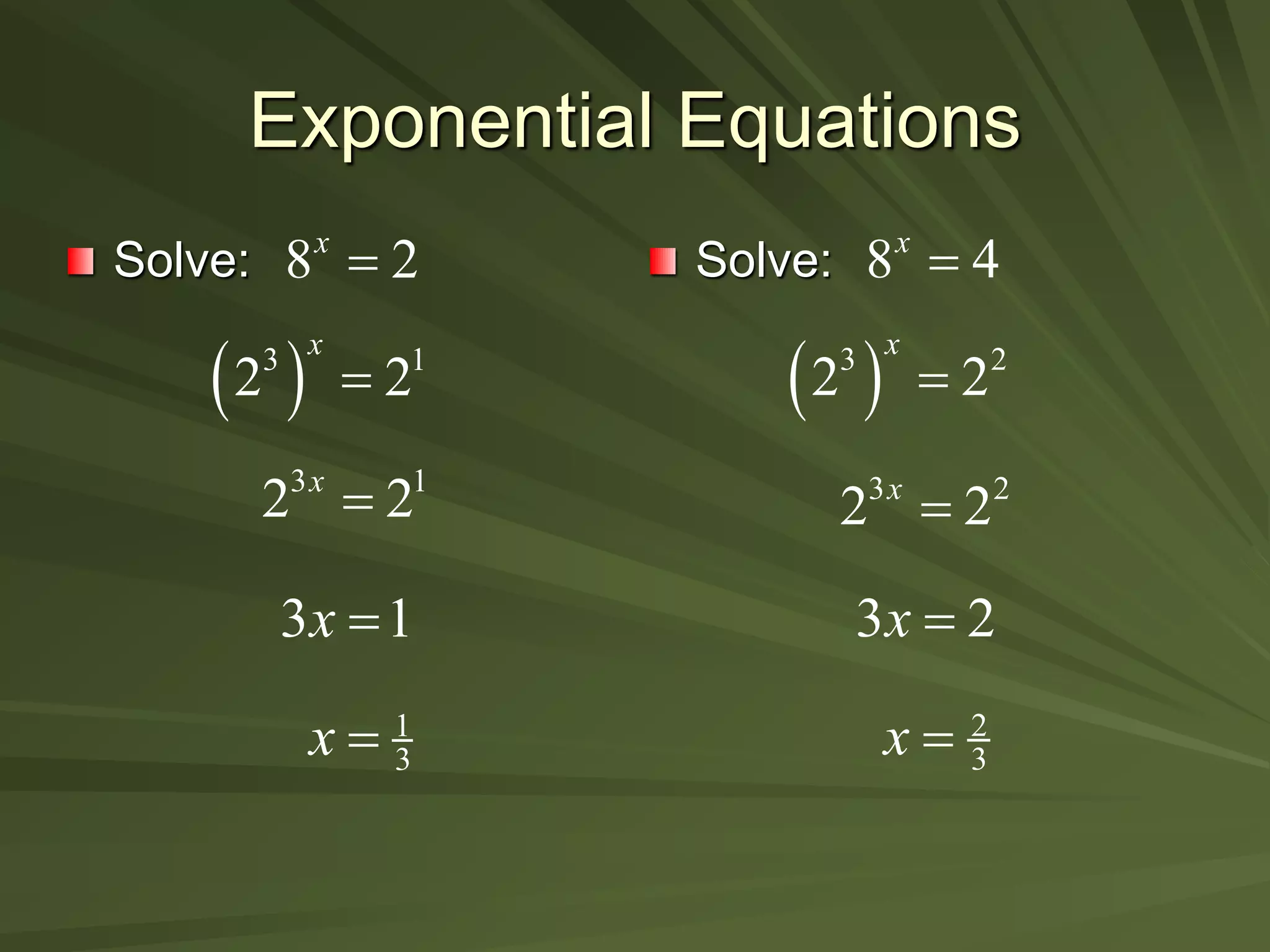This document discusses exponential functions. It begins by stating the objectives of understanding properties of exponents, simplifying exponential expressions, solving exponential equations, and sketching graphs of exponential functions. It then defines exponential functions and discusses their general form. Several properties of exponents are listed and examples of simplifying expressions using these properties are shown. The document also demonstrates how to solve various exponential equations. Finally, it discusses graphing and properties of exponential functions, including the special number e and the exponential function with base e.

1. Exponential Functions

2. Objectives
To use the properties of exponents to:
 Simplify exponential expressions.
 Solve exponential equations.
To sketch graphs of exponential functions.

3. Exponential Functions
A polynomial function has the basic form: f (x) = x3
An exponential function has the basic form: f (x) = 3x
An exponential function has the variable in the
exponent, not in the base.
General Form of an Exponential Function:
f (x) = Nx, N > 0

4. Properties of Exponents
X Y
A A
  X Y
A 
XY
A
X Y
A 
 
Y
X
A 
X
Y
A
A

 
X
AB  X X
A B
X
A
B
 

 
 
X
X
A
B
X
A

1
X
A
1
X
A
 X
A
X
Y
A  Y X
A  
X
Y
A


5. Properties of Exponents
2 3
2 2
 
5
2 32

2 6
2 2
  4
2
4
1
2

1
16

 
2
3
2  6
2 64

Simplify:

6. Properties of Exponents
3
2
3

 

 
 
3
3
2
3


3
3
3
2

7
9
3
3

2
3
2
1
3

1
9

  
1 1
2 2
2 8 
1
2
16 16

27
8

4

 
1
2
2 8
 
Simplify:

7. Exponential Equations
Solve: Solve:
5 125
x

3
5 5
x

3
x 
1
2
( 1)
7 7
x 


1
2
1
x   
1
2
x 

8. Exponential Equations
8 4
x

 
3 2
2 2
x

3 2
x 
2
3
x 
3 2
2 2
x

8 2
x

 
3 1
2 2
x

3 1
x 
1
3
x 
3 1
2 2
x

Solve: Solve:

9. Exponential Equations
1
3
27
x 
 
1
3
3
3
27
x 
19,683
x 
 
1
3 27
x

 
1
3 27
x


3
x
 
3
x  
3
3 3
x


Not considered an
exponential equation,
because the variable
is now in the base.
Solve: Solve:

10. Exponential Equations
3
4
8
x 
 
4
3 4
3
3
4
8
x 
 
4
3
8
x 
 
4
2
x 
16
x 
Not considered an
exponential equation,
because the variable
is in the base.
Solve:

11. Exponential Functions
General Form of an Exponential Function:
f (x) = Nx, N > 0
g(x) = 2x
x
2x
g(3) =
g(2) =
g(1) =
g(0) =
g(–1) =
g(–2) =
8
4
2
1 1
2 1
2

2
2
2
1
2
 1
4


12. Exponential Functions
g(x) = 2x
2
0
x 3 2 1 0 -1 -2
g(x) 8 4 2 1 1/2 1/4

13. Exponential Functions
g(x) = 2x

14. Exponential Functions
h(x) = 3x
x
2
1
0
9
3
1
 
h x
–1
–2
1
3
1
9

15. Exponential Functions
h(x) = 3x

16. Exponential Functions
Exponential functions with
positive bases greater than
1 have graphs that are
increasing.
The function never crosses
the x-axis because there is
nothing we can plug in for x
that will yield a zero
answer.
The x-axis is a horizontal
asymptote.
h(x) = 3x (red)
g(x) = 2x (blue)

17. Exponential Functions
A smaller base means the
graph rises more
gradually.
A larger base means the
graph rises more quickly.
Exponential functions will
not have negative bases.
h(x) = 3x (red)
g(x) = 2x (blue)

18. Exponential Functions
   
1
2
x
j x 
Exponential functions with positive
bases less than 1 have graphs that are
decreasing.

19. Properties of graphs of
exponential functions
Function and 1 to 1
y intercept is (0,1) and no x
intercept(s)
Domain is all real numbers
Range is {y|y>0}
Graph approaches but does not
touch x axis – x axis is asymptote
Growth or decay determined by base

20. The Number e
e  2.71828169
A base often associated with exponential functions is:

21. The Number e
Compute:  
1
0
lim 1 x
x
x


x
–.1
–.01
–.001
2.868
2.732
2.7196
 
1
1 x
x

 
1
0
lim 1 x
x
x



x
.1
.01
.001
2.5937
2.7048
2.7169
 
1
1 x
x

 
1
0
lim 1 x
x
x



2.71828169


22. The Number e
Euler’s number
Leonhard Euler
(pronounced “oiler”)
Swiss mathematician
and physicist

23. The Exponential Function
f (x) = ex

24. Exponential Functions
x
2
1
0
4
2
1
 
j x
–1
–2
1
2
1
4
   
1
2
x
j x 

25. Why study exponential functions?
Exponential functions are used in our real world
to measure growth, interest, and decay.
Growth obeys exponential functions.
Ex: rumors, human population, bacteria,
computer technology, nuclear chain reactions,
compound interest
Decay obeys exponential functions.
Ex: Carbon-14 dating, half-life, Newton’s Law of
Cooling