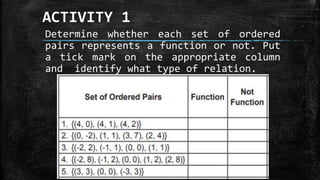
The document discusses domain and range of functions. It provides examples of determining the domain and range from graphs of functions and from algebraic rules that define functions. The domain of a function is the set of permissible input values, while the range is the set of permissible output values. Examples show how to identify the domain and range from graphs by considering limits, and how to determine them algebraically by manipulating equations to solve for variables.

1. Domain and Range
of a Function

2. Objectives:
▪ Illustrates function notation.
▪ Finds domain and range of a function.
▪ Appreciates the concept of domain and range
of a function.

3. ACTIVITY 1
Determine whether each set of ordered
pairs represents a function or not. Put
a tick mark on the appropriate column
and identify what type of relation.

4. Function Notation
The f(x) notation can also be used to define a
function. If f is a function, the symbol f(x), read as “f of x,”
is used to denote the value of the function f at a given
value of x. In simpler way, f(x) denotes the y-value
(element of the range) that the function f associates with
x-value (element of the domain). Thus, f(1) denotes the
value of y at x = 1. Note that f(1) does not mean f times 1.
The letters such as g, h and the like can also denote
functions.

5. Function Notation
Furthermore, every element x in the
domain of the function is called the pre-
image. However, every element y or f(x) in
the range is called the image. The figure at
the right illustrates concretely the input (the
value of x) and the output (the value of y or
f(x)) in the rule or function. It shows that for
every value of x there corresponds one and
only one value of y.

6. Function Notation
Example:
Consider the rule or the function f defined by
f(x) = 3x – 1. If x = 2, what will be the value of the
function?
Solution:
f(x) = 3x – 1 Rule/Function
f(2) = 3(2) – 1 Substituting x by 2
f(2) = 6 – 1 Simplification
f(2) = 5 Simplification
Therefore, the input is 2 (the
value of x) and the output is 5
(the value of y or f(x)).

7. Function Notation
Example:
Consider the rule or the function f defined by
f(x) = 3x – 1. What will be the value of the
function if x = 3?
Solution:
f(x) = 3x – 1 Rule/Function
f(3) = 3(3) – 1 Substituting x by 3
f(3) = 9 – 1 Simplification
f(3) = 8 Simplification
Therefore, the input is 3 (the
value of x) and the output is 8
(the value of function).

8. Domain and Range of a Function
In the previous section, you have learned how the
domain and the range of a relation are defined. The
domain of the function is the set of all permissible values
of x that give real values for y. Similarly, the range of the
function is the set of permissible values for y or f(x) that
give the values of x real numbers.

9. Domain and Range of a Function
You have taken the domain and the
range of the relation given in the table of
values in the previous lesson, the set of
ordered pairs and the graph.
Can you give the domain and the range if
the graph of the function is known? Try this
one!

10. Illustrative Examples:
If you are given the graph, how can you determine the
domain and the range?

11. Illustrative Examples:
Solutions: In (a), arrow heads indicate
that the graph of the function extends
in both directions. It extends to the left
and right without bound; thus, the
domain D of the function is the set of
real numbers. Similarly, it extends
upward and downward without bound;
thus, the range R of function is the set
of all real numbers. In symbols,

12. Illustrative Examples:
Solutions: In (b), arrow heads indicate
that the graph of the function is
extended to the left and right without
bound, and downward, but not upward,
without bound. Thus, the domain of the
function is the set of real numbers,
while the range is any real number less
than or equal to 0.That is,

13. Illustrative Examples:
Given the rule, we can find the domain and range of a
function algebraically.
c. Consider the function f (x) = x + 1.
We can substitute x with any real number that does
not make the function undefined. Therefore, the domain
is the set of real numbers. To find range, we let y = f (x) = x
+ 1 and solve for x in terms of y. In symbols,
𝑫 = 𝒙 𝒙 ∈ 𝕽

14. Illustrative Examples:
Given the rule, we can find the domain and range of a
function algebraically.
c) Consider the function f (x) = x + 1.
To find range, we let y = f (x) = x + 1 and solve for x in
terms of y.
Thus, -x = - y + 1 or x = y - 1 ; which can be defined for
any real number y. Therefore, the range of f (x) is the set
of real numbers.That is,
𝑹 = 𝒚 𝒚 ∈ 𝕽

15. Illustrative Examples:
Given the rule, we can find the domain and range of a
function algebraically.
d) If the function is in the form of a quotient like 𝑓 𝑥 =
4
𝑥−4
.
We have to take note that rational expression should
not have the denominator zero, therefore, 𝑥 here should not
be equal to 4, but other real numbers can be possible value of
𝑥
𝑫 = 𝒙 𝒙 ∈ 𝕽, 𝒙 ≠ 𝟒

16. Illustrative Examples:
Given the rule, we can find the domain and range of a function
algebraically.
d) If the function is in the form of a quotient like 𝑓 𝑥 =
4
𝑥−4
.
To find the range, let 𝑓 𝑥 =
4
𝑥−4
and then solve for 𝑥 in
terms of 𝑦. Solving for 𝑥 =
4𝑦+4
𝑦
, which is undefined for 𝑦 = 0.
Therefore, the range consists of nonzero real numbers.
𝑹 = 𝒚 𝒚 ∈ 𝕽, 𝒚 ≠ 𝟎