Dokumen ini membahas metode interpolasi linier, yang digunakan untuk memperkirakan nilai di antara titik data yang diketahui. Dalam metode ini, garis lurus menghubungkan dua titik untuk menentukan nilai baru, dan contoh aplikasi praktis termasuk perkiraan jumlah penduduk pada tahun tertentu. Metode ini juga dibahas dalam konteks interpolasi polinomial yang lebih umum.

1. METODE NUMERIK
“METODE INTERPOLASI LINIER”
Dosen Pembimbing :
Siti Dinarti S.Pd, M.Pd
Disusun Oleh :
OKTI AGUNG PAMBUDI (1251155)
PRODI PENDIDIKAN MATEMATIKA
SEKOLAH TINGGI KEGURUAN DAN ILMU PENDIDIKAN
PERSATUAN GURU REPUBLIK INDONESIA
JOMBANG
2015

2. INTERPOLASI
A. PENDAHULUAN
Dalam interpolasi dicari suatu nilai yang berada di antara beberapa titik data yang
telah diketahui nilainya. Untuk dapat memperkirakan nilai tersebut, pertama kali dibuat
suatu fungsi atau persamaan yang melalui titik-titik data. Setelah persamaan garis/kurva
terbentuk, kemudian dihitung nilai fungsi yang berada di antara titik-titik data. Kurva
pada Gambar 5.1.a menggunakan segmen garis lurus atau interpolasi linier untuk
menghubungkan titik-titik data, Gambar 5.1.b menggunakan kurva untuk
menghubungkan titik-titik data.
Metode interpolasi yang paling banyak digunakan adalah interpolasi polynomial.
Persamaan polinomial adalah persamaan aljabar yang mengandung jumlah dari variable
𝑥 berpangkat bulat (integer). Bentuk umum persamaan polinomial adalah :
( )f x ● ( )f x ●
● ●
● ●
● ●
x
(a) (b)
Gambar 5.1 Interpolasi a,b
𝒇( 𝒙) = 𝒂 𝟎 + 𝒂 𝟏 𝒙 + 𝒂 𝟐 𝒙 𝟐
+ … + 𝒂 𝒏 𝒙 𝒏
Dengan 𝑎0, 𝑎1, 𝑎2, … 𝑎 𝑛 adalah parameter yang akan dicari berdasaran titik data; n
adalah derajad (order) dari persamaan polinomial , dan 𝑥 adalah variable bebas.
Untuk 𝑛 + 1 titik data, hanya terdapat satu polinomial order 𝑛 atau kurang yang
melalui semua titik. Misalnya, hanya ada satu garis lurus (polinomial order 1) yang
menghubungkan dua titik (Gambar 5.2.a). demikian juga tiga titik buah dapat

3. dihubungkan oleh fungsi parabola (polinomial order 2), sedang untuk empat titik dapat
dilalui kurva polinomial order tiga , seperti terlihat dalam Gambar 5.2 c. Di dalam operasi
interpolasi ditentukan suatu persamaan polinomial order 𝑛 yang melalui 𝑛 + 1 titik data,
yang kemudian digunakn untuk menentukan suatu nilai di antara titik data tersebut. Pada
polinomial berderajad satu, diperoleh bentuk interpolasi linier yang sudah banyak
dikenal, metode tersebut mempunyai bentuk sederhana dan mudah dipahami.
y y
● ●
●
● ●
x x
a. order 1 menghubungkan 2 titik b. order 2 menghubungkan 3 titik
y
● ●
●
●
c. order 3 menghubungkan 4 titik x
Gambar 5.2 Interpolasi Polinomial
B. METODE INTERPOLASI LINIER
Bentuk paling sederhana dari interpolasi adalah menghubungkan dua buah titik
data dengan garis lurus. Metode ini disebut denagn interpolasi linier yang dapat
dijelaskan dengan menggunakan Gambar 5.3

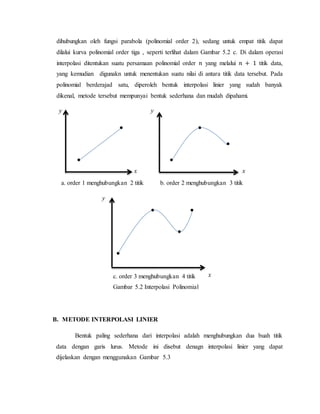
4. Diketahui nilai suatu fungsi di titik 𝑥0 dan 𝑥1, yaitu 𝑓(𝑥0 ) dan 𝑓( 𝑥1). Dengan
metode interpolasi linier akan dicari nilai fungsi di titik 𝑥, yaitu 𝑓1(𝑥). Indeks 1 pada
𝑓1(𝑥) menunjukkan bahwa interpolasi dilakukan dengan interpolasi polinomial order 1.
Dari dua segitiga sebangun ABC dan ADE seperti tampak dalam Gambar 5.3,
terdapat hubungan berikut :
𝐵𝐶
𝐴𝐵
=
𝐷𝐸
𝐴𝐷
𝑓1( 𝑥)− 𝑓(𝑥0 )
𝑥−𝑥0
=
𝑓( 𝑥1)−𝑓(𝑥0 )
𝑥1− 𝑥0
𝑓( 𝑥)
𝑓( 𝑥1) E
𝑓1( 𝑥) C
𝑓( 𝑥0)
A B D
𝑥0 𝑥 𝑥1
Gambar 5.3 Interpolasi Linier
𝑓1 ( 𝑥) − 𝑓( 𝑥0 ) =
[ 𝑓( 𝑥1)− 𝑓( 𝑥0 )].( 𝑥 − 𝑥0)
𝑥1 − 𝑥0
𝑓1 ( 𝑥) = 𝑓( 𝑥0 ) +
[ 𝑓( 𝑥1)− 𝑓( 𝑥0 )].( 𝑥 − 𝑥0)
𝑥1 − 𝑥0
Cara penulisan 𝑓1( 𝑥) menunjukkan bahwa ini adalah polinom interpolasi orde satu
(interpolasi linier). Suku [𝑓(𝑥1) − 𝑓(𝑥0)]/(𝑥1 − 𝑥0)] adalah kemiringan garis yang
menghubungkan dua titik data dan merupakan perkiraan beda hingga turunan pertama.
Semakin kecil interval antara titik data, hasil perkiraan akan semakin baik.

5. Algoritma Interpolasi Linier
1. Tentukan nilai 𝑥0, 𝑦0, 𝑥1,dan 𝑦1.
2. Periksa apakah 𝑥0 = 𝑥1. Jika ya, maka kembali ke langkah 1 sebab nilai fungsinya
tidak terdefinisi dalam kondisi ini. Jika tidak, maka dilanjutkan ke langkah 3.
3. Masukkan nilai 𝑥.
4. Periksa apakah min{x0 , x1} ≤ x ≤ max{x0, x1}. Jika tidak, maka masukkan nilai 𝑥
yang lain. Jika ya, maka dilanjutkan langkah 5.
5. Hitung 𝑓1( 𝑥) = 𝑦0 +
(𝑦1− 𝑦0)(𝑥− 𝑥0)
𝑥1− 𝑥0
6. Periksa apakah y0 = y1. Karena jika sama, maka akan diperoleh 𝑓1( 𝑥) = 𝑦0.
7. Tulis hasil 𝑦 = 𝑓1
( 𝑥)
Contoh
1. Perkirakan atau prediksi jumlah penduduk Gunungpati pada tahun 2005 berdasarkan data
tabulasi berikut:
Tahun 2000 2010
Jumlah Penduduk 179.300 203.200
Penyelesaian:
Diketahui: x0 = 2000, x1 = 2010, y0 = 179.300, y1 = 203.200.
Ditanya: Prediksi jumlah penduduk Gunungpati pada tahun 2005.
𝑓1( 𝑥) = 𝑦0 +
(𝑦1
− 𝑦0)(𝑥 − 𝑥0)
𝑥1 − 𝑥0
Misalkan 𝑥 = 2005
𝑓1(2005) = 179.300+
(203.200− 179.300)(2005− 2000)
2010− 2000
𝑓1(2005) = 191.250
Jadi, diperkirakan jumlah penduduk Gunungpati pada tahun 2005 adalah 191.250 orang.

6. 2. Dicari nilai ln 2 dengan metode interpolasi linier berdasarkan data ln 1 = 0 dan ln 6 =
1,7917595. Hitunglah juga nilai tersebut berdasarkan data ln 1 dan ln 4 = 1,3862944.
Untuk membandingkan hasil yang diperoleh, diketahui nilai eksak dari ln 2 =
0,69314718.
Penyelesaian:
Diketahui : ln 1 = 0 ; ln 6 = 1,7917595 ; ln 4 = 1,3862944. ;
nilai eksak dari ln 2 = 0,69314718
Ditanya : Hitunglah juga nilai ln 2 dan bandingkan hasil yang diperoleh .
Misalkan :
𝑛𝑖𝑙𝑎𝑖 ln 𝑝𝑎𝑑𝑎 𝑥 = 2
𝑛𝑖𝑙𝑎𝑖 ln 𝑑𝑖 𝑥0 = 1 𝑑𝑎𝑛 𝑥1 = 6
𝑓1(2) = 0 +
(1,7917595− 0)(2− 1)
6 − 1
= 0,35835190
Besar kesalahan adalah :
𝐸𝑡 =
0,69314718 − 0,3585190
0,69314718
× 100% = 48,3%
Apabila digunakan interval yang lebih kecil,yaitu nilai 𝑥0 = 1 𝑑𝑎𝑛 𝑥1 = 4 maka :
𝑓1(2) = 0 +
(1,3862944− 0)(2− 1)
4 − 1
= 0,46209813
Besar kesalahan adalah :
𝐸𝑡 =
0,69314718 − 0,46209813
0,69314718
× 100% = 33,3%
Terlihat bahwa dengan menggunakn interval yang lebih kecil diperoleh hasil yang lebih
baik (kesalahan lebih kecil)

7. 3. Perkirakan jumlah penduduk Korea Selatan tahun 1968 berdasarkan data tabulasi berikut:
Tahun 1960 1970
Jumlah Penduduk (juta) 179.3 203.2
Penyelesaian :
Diket : Tahun 1960 = 179.3 juta jiwa
Tahun 1970 = 203.2 juta jiwa
Ditanya : Taksiran jumlah penduduk Korea Selatan tahun 1968
𝑓1(1968) = 179.3 +
(203.2 − 179.3)(1968 − 1960)
1970 − 1960
= 198.4
Jadi taksiran jumlah penduduk Korea Selatan tahun 1968 adalah 198.4 juta jiwa

8. DAFTAR PUSTAKA
Fuad Yusuf.1994.METODE NUMERIK 1.University Press IKIP Surabaya : Surabaya
Triatmodjo,Bambang.1992.METODE NUMERIK.Beta Offet : Jogjakarta
http://risqi.blog.com/files/2010/12/MODUL-MATA-KULIAH3.pdf
http://s3.amazonaws.com/ppt-download/makalahinterpolasikelompok2-121119021744-
phpapp01.docx?response-content-
disposition=attachment&Signature=emyuZTQQVJo7RBjgNUR6UWmKoBY%3D&Expi
res=1427464606&AWSAccessKeyId=AKIAIA7QTBOH2LDUZRTQ