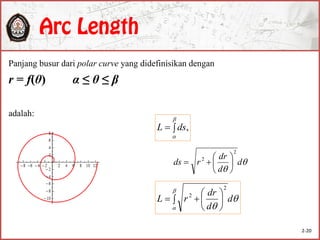
1. Materi ini membahas sistem koordinat polar dan kurva polar dalam kalkulus peubah banyak. 2. Sistem koordinat polar menggunakan jarak (r) dan sudut (θ) untuk merepresentasikan posisi suatu titik dalam bidang dua dimensi. 3. Kurva polar didefinisikan oleh persamaan r = f(θ) yang menggambarkan hubungan antara jarak dan sudut.

1. Instructor:
M. Mujiya Ulkhaq
Department of Industrial Engineering
Polar Coordinates & Polar Curves
Kalkulus Peubah Banyak
Multivariable Calculus

2. • Definisi sistem koordinat polar (kutub);
• Mengubah koordinat polar ke koordinat kartesius dan sebaliknya;
• Kurva polar;
• Gradien garis singgung kurva polar;
• Luas area yang dilingkupi kurva polar;
• Panjang busur kurva polar;
• Luas permukaan dari kurva polar yang diputar terhadap sumbu tertentu.
2-2

3. Sistem koordinat merepresentasikan posisi sebuah titik dalam suatu bidang (atau
ruang) dengan satu atau satu pasang bilangan yang disebut koordinat.
Terdapat beberapa sistem koordinat:
[1D] sistem koordinat garis:
[2D] sistem koordinat kartesius: [2D] sistem koordinat polar:
2-3

4. Sistem Koordinat Polar merepresentastikan posisi sebuah titik dalam suatu bidang
dua dimensi dengan sepasang bilangan (r, θ):
• r merupakan jarak antara titik tsb dengan titik
asal (pole/origin);
• θ merupakan sudut (dalam satuan radian) yang
dibentuk antara sumbu polar dengan OP.
Secara konvensional, sudut θ bernilai positif
ketika diukur berlawanan arah dari jarum jam
dari sumbu polar; begitu pula sebaliknya.
Ketika r > 0, maka titik berada dalam kuadran
yang sama dengan θ; begitu pula sebaliknya.(–r, θ) = (r, θ + π)
2-4

5. Contoh 2.1
Plot titik-titik berikut ke dalam sistem koordinat polar!
a. (1, 5π/4) b. (2, 3π) c. (2, –2π/3) d. (–3, 3π/4)
a. b.
c. d.
2-5

6. Dalam sistem koordinat kartesius, setiap titik hanya diwakili SATU pasang
bilangan yang merepresentasikan posisinya. Namun, dalam sistem koordinat polar,
satu titik dapat dilambangkan dalam LEBIH DARI SATU pasang bilangan.
Titik (1, 5π/4) dapat direpresentasikan dengan:
(r, θ)
(r, θ + 2nπ)
(–r, θ + (2n + 1)π)*n adalah integer (bilangan bulat) 2-6

7. Contoh 2.2
Ubah posisi titik berikut dari koordinat polar ke koordinat kartesius (2, π/3)!
x = r cos θ = 2 cos (π/3) = 1; y = r sin θ = 2 sin(π/3) = √3
Posisi dalam koordinat kartesius = (1, √3)
Contoh 2.3
Ubah posisi titik berikut dari koordinat kartesius ke koordinat polar (1, –1)!
Posisi dalam koordinat polar = (√2, –π/4) atau (√2, 7π/4)


cos
;cos
rx
r
x




sin
;sin
ry
r
y


x
y
ryx


tan
;222
  ;211
2222
 yxr ;111tan  xy 47atau4  
«»
2-7

8. Persamaan polar curve: r = f(θ)
Garis
cos
a
r 
Garis linier melalui titik asal (y = mx) → θ = α,
α merupakan konstanta sudut (satuan radian)
sin
b
r 
 cossin m
c
r

Garis linier tidak melalui titik asal (y = mx + c) →
Garis vertikal (x = a) →
Garis horisontal (y = b) →
2-8

9. Contoh 2.4
Ubah dalam koordinat polar garis berikut:
a. y = –x b. y = – 3 c. x = 4
y = –x
y/x = –1
tan θ = –1
tan–1 (tan θ) = tan–1 (–1)
θ = 3π/4
a.
y = –3
r sin θ = –3
r = –3/sin θ
b.
x = 4
r cos θ = 4
r = 4/cos θ
c.
2-9

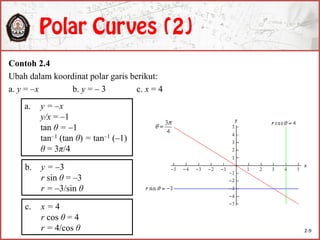
10. Persamaan polar curve: r = f(θ)
Lingkaran
Titik pusat di titik asal [0,0] dengan radius a → r = a
Titik pusat di titik [a, 0] dengan radius |a|→ r = 2a cos θ
Titik pusat di titik [0, b] dengan radius |b| → r = 2b sin θ
2-10
Titik pusat di titik [a, b] dengan radius → r = 2a cos θ + 2b sin θ22
ba 

11. Contoh 2.5
Gambarkan polar curve berikut ini:
a. r = 7 b. r = 4 cos θ c. r = –7 sin θ
2-11

12. Latihan 2.1
Sketsa polar curve berikut ini dalam koordinat polar:
r = 1 + sin θ 0 ≤ θ ≤ 2π
Latihan 2.2
Sketsa polar curve berikut ini dalam koordinat polar:
r = cos 2θ 0 ≤ θ ≤ 2π
Latihan 2.3
Sketsa polar curve berikut ini dalam koordinat polar:
r = 2 + 4 cos θ 0 ≤ θ ≤ 2π
2-12

13. Dalam command window, tuliskan:
syms theta %mendefinisikan parameter theta
ezpolar(r,[a,b]) %menggambar polar curve
Keterangan: r = f(θ); a = initial point (theta); b = terminal point (theta)
Contoh:
syms theta
ezpolar(2*cos(3*theta/2),[0,4*pi])
2-12d
*MATLAB versi 2012a
0.5
1
1.5
2
30
210
60
240
90
270
120
300
150
330
180 0
r = 2 cos((3 )/2)

14. Untuk menentukan garis singgung dari polar curve, r = f(θ), θ akan dianggap
sebagai suatu parameter, sehingga persamaan parametrik akan ditulis dengan:
Maka, turunan pertama yang merupakan gradien dari garis singgung didefinisikan
dengan:
x = r cos θ = f(θ) cos θ y = r sin θ = f(θ) sin θ






sincos
cossin
r
d
dr
r
d
dr
d
dx
d
dy
dx
dy
m



Kurva mempunyai garis singgung horisontal bila:
dy/dθ = 0 (diberikan dx/dθ ≠ 0)
Kurva mempunyai garis singgung vertikal bila:
dx/dθ = 0 (diberikan dy/dθ ≠ 0) 2-14

15. Contoh 2.6
Cari gadien garis singgung pada polar curve r = 3 + 8 sin θ pada θ = π/6.
Gradien garis singgung:
  
  
     
      5
311
6sin86sin36cos8
6cos36sin6cos16
sin8sin3cos8
cos3sincos16
sinsin83coscos8
cossin83sincos8
sincos
cossin
2222























m
r
d
dr
r
d
dr
m
2-15

16. Luas area (A) yang dilingkupi polar curve yang didefinisikan dengan
r = f(θ) α ≤ θ ≤ β
adalah:



drA
2
1 2
A
2-16

17. Contoh 2.7
Cari luas area four-leaved rose (r = cos 2θ) dari θ = –π/4 sampai θ = π/4
      
8
24
1
sinsin
4
1
44
4
1
4sin
4
1
4
1
4cos1
4
1
4cos
2
1
2
1
2
1
2cos
2
1
2
1
4
4
4
4
4
4
4
4
2
4
4
2




































 
 







A
A
A
A
dA
dA
dA
drA
2-17

18. Luas area (A) yang di antara dua polar curve yang didefinisikan dengan
r1 = f(θ) dan r0 = g(θ) α ≤ θ ≤ β
adalah:
  


drrA
2
1 2
1
2
0
A
2-18

19. Latihan 2.4
Tentukan luas area sbb:
di dalam r = 3 + 2 sinθ
di luar r = 2
Latihan 2.5
Tentukan luas area sbb :
di luar r = 3 + 2 sinθ
di dalam r = 2
2-19

20. Panjang busur dari polar curve yang didefinisikan dengan
r = f(θ) α ≤ θ ≤ β
adalah:
,


dsL


d
d
dr
rds
2
2







 










d
d
dr
rL
2
2
2-20

21. Contoh 2.8
Cari panjang busur dari polar curve dengan persamaan sbb:
r = 3 sin θ 0 ≤ θ ≤ π/3
   
 
 
 













 
 
 
 
L
L
dL
dL
dL
dL
3
0
3
0
22
3
0
22
3
0
22
3
0
22
3
cossin3
cossin9
cos9sin9
cos3sin3
1
2
3
30
210
60
240
90
270
120
300
150
330
180 0
r = 3 sin()
2-21

22. Luas permukaan dari polar curve yang didefinisikan dengan
r = f(θ) α ≤ θ ≤ β
• yang diputar terhadap sumbu-polar adalah:
• yang diputar terhadap sumbu-y adalah:





 dsrydsS sin22





 dsrxdsS cos22
Note that because we will pick up
a dθ from the ds, we’ll need to
substitute one of the parametric
equations in for polar or y
depending on the axis of rotation.
This will often mean that the integrals
will be somewhat unpleasant.
2-22

23. Contoh 2.9
Tentukan luas permukaan yang dibentuk dari polar curve yang dirotasi terhadap
sumbu-polar dengan persamaan sbb :
r = sin θ 0 ≤ θ ≤ π
 
2
0
0
0
2
0
22
0
22
2sin
2
1
2cos1
2
1
2
sin2
cossinsinsin2
cossin2



















 

 
 
S
S
dS
dS
dS
drrS
0.2
0.4
0.6
0.8
1
30
210
60
240
90
270
120
300
150
330
180 0
r = sin()
2-23

24. Latihan 2.6
Cari gradien garis singgung pada polar curve yang mempunyai persamaan sbb:
r = 4 sin θ cos θ pada titik θ = π/6
Latihan 2.7
Cari gradien garis singgung pada polar curve yang mempunyai persamaan sbb:
r = θ – cos θ pada titik θ = 3π/4
Latihan 2.8
Cari panjang busur dari polar curve yang mempunyai persamaan sbb:
r = –4 sin θ 0 ≤ θ ≤ π
2-24

25. Instructor:
M. Mujiya Ulkhaq
Department of Industrial Engineering
Kalkulus Peubah Banyak
Multivariable Calculus
Thank You for Your Attention