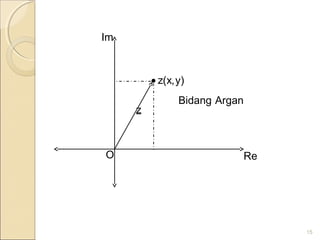
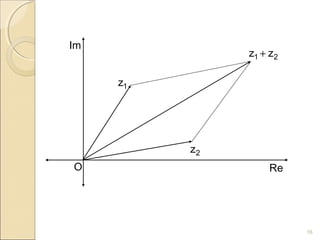
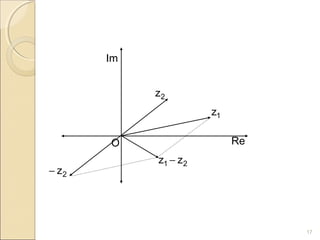
Dokumen tersebut membahas tentang sistem bilangan riil dan kompleks. Bilangan kompleks didefinisikan sebagai bilangan berbentuk a + bi, dimana a dan b adalah bilangan riil dan i^2 = -1. Bilangan kompleks dapat digambarkan secara geometris sebagai titik pada bidang kompleks dan operasi aljabar bilangan kompleks memiliki interpretasi geometris.

1. FUNGSI KOMPLEKS
1

2. BAB 1BAB 1
ReviewReview
Sistem Bilangan RiilSistem Bilangan Riil
System bilangan yang kita kenal selama ini dapat dijabarkan menjadi:
 Bilangan asli: 1, 2, 3, 4, …………..,
Himpunan bilangan asli dinotasikan N={1, 2, 3, …………….}
 Bilangan Cacah ; 0,1,2 3, 4, …
Himpunan Cacah asli dinotasikan C = {1, 2, 3, …………….}
 Bilangan bulat
Himpunan bilangan bulat ditulis Z = {……, -3, -2, -1, 0, 1, 2, 3,………..}
 Bilangan rasional (Q) adalah bilangan yang dapat ditulis sebagai
dengan bentuk p/q, p disebut pembilang dan q disebut penyebut.
 Bilangan irrasional (I) yaitu bilangan yang bukan bilangan rasional, atau
bilangan yang tidak dapat dinyatakan sebagai p/q .
 Bilangan riil dapat dilukiskan pada suatu garis lurus yang disebut
sumbu riil atau garis bilangan dinotasikan .
2
IQR ∪=

3. BILANGAN KOMPLEKS
Kenapa butuh atau ada bilangan kompleks?
Dengan memiliki sistem bilangan real ℝ saja kita
tidak dapat menyelesaikan persamaan x2
+1=0. Jadi
disamping bilangan real kita perlu bilangan jenis
baru.
Bilangan jenis baru ini dinamakan bilangan imajiner
atau bilangan kompleks.
3

4. BILANGAN KOMPLEKS DAN OPERASINYA
Definisi 1
Bilangan kompleks adalah bilangan yang berbentuk:
a + bi atau a + ib, a dan b bilangan real dan i2
= –1.
Notasi
Bilangan kompleks dinyatakan dengan huruf z,
sedang huruf x dan y menyatakan bilangan real. Jika
z = x + iy menyatakan sembarang bilangan kompleks,
maka x dinamakan bagian real dan y bagian imajiner
dari z. Bagian real dan bagian imaginer dari bilangan
kompleks z biasanya dinyatakan dengan Re(z) dan
Im(z).
4

5. OPERASI HITUNG PADA BILANGAN
KOMPLEKS
DEFINISI 2
Bilangan kompleks z1=x1+iy1 dan bilangan kompleks
z2=x2+iy2 dikatakan sama, z1=z2, jika dan hanya jika
x1=x2 dan y1=y2.
DEFINISI 3
Untuk bilangan kompleks z1=x1+iy1 dan z2=x2+iy2
jumlah dan hasilkali mereka berturut-turut
didefinisikan sbb:
z1+z2 = (x1+x2) + i(y1+y2)
z1 •z2 = (x1x2 – y1y2) + i(x1y2+x2y1) 5

6. Operasi-Operasi Aljabar Pada BilanganOperasi-Operasi Aljabar Pada Bilangan
KompleksKompleks
 Penambahan
 Pengurangan
 Perkalian
 Pembagian
6
( ) ( )
( ) ( )
a ib c id a ib c id
a c i b d
+ + + = + + +
= + + +
( ) ( )
( ) ( )
a ib c id a ib c id
a c i b d
+ − + = + − −
= − + −
2
( ) . ( ) .
( ) ( )
a ib c id ac a id ibc bdi
ac bd i ad bc
+ + = + + +
= − + +
2
1i = −
2
2 2 2
2 2
2 2 2 2
. .
.
( )
.
a ib a ib c id ac a id i bc i bd
c id c id c id c d i
ac bd i bc ad
c d
ac bd bc ad
i
c d c d
+ + − − + −
= =
+ + − −
+ + −
=
+
+ −
= +
+ +

7. Himpunan semua bilangan kompleks diberi notasi ℂ
Jadi ℂ = { z | z = x + iy, x∈ℝ, y∈ℝ }.
Jika Im(z)=0 maka bilangan kompleks z menjadi
bilangan real x, sehingga bilangan real adalah keadaan
khusus dari bilangan kompleks, sehingga ℝ⊂ℂ.
Jika Re(z)=0 dan Im(z)≠0, maka z menjadi iy dan
dinamakan bilangan imajiner murni. Bilangan imajiner
murni dengan y=0, yakni bilangan i, dinamakan satuan
imajiner.
7

8. Sifat-sifat lapangan bilangan kompleks
Himpunan semua bilangan kompleks bersama operasi
penjumlahan dan perkalian (ℂ ,+,•) membentuk sebuah
lapangan (field). Adapun sifat-sifat lapangan yang berlaku
pada bilangan kompleks z1,z2 dan z3 adalah sebagai berikut:
1. z1+z2∈ℂ dan z1•z2∈ℂ . (sifat tertutup)
2. z1+z2= z2+z1 dan z1•z2= z2•z1 (sifat komutatif)
3. (z1+z2)+z3= z1+(z2+z3) dan (z1•z2) •z3= z1•(z2•z3)
(sifat assosiatif)
4. z1•(z2+z3)=(z1•z2)+(z1•z3) (sifat distribtif)
5. Ada 0=0+i0∈ℂ , sehingga z+0=z (0 elemen netral
penjumlahan)
8

9. 6. Ada 1=1+i0∈ℂ , sehingga z•1=z (1elemen netral
perkalian
7. Untuk setiap z=x+iy∈ℂ, ada –z=–x–iy
sehingga z+(–z)=0
8. Untuk setiap z=x+iy∈ℂ, ada z-1
=sehingga z•z-1
=1.
Tugas: Buktikan sifat-sifat 1 – 8 menggunakan definsi
yang telah diberikan.
9

10. soal:
1. Jika z1=x1+iy1 dan z2=x2+iy2,
buktikan bahwa: z1 –z2= (x1 – x2)+i(y1 –y2)
2. Diketahui: z1=2+3i dan z2=5–i.
tentukan z1
+z2, z1
–z2 ,z1
z2, dan
10
2
1
z
z

11. Kompleks Sekawan
Jika z = x + iy bilangan kompleks, maka bilangan
kompleks sekawan dari z ditulis , didefinisikan
sebagai = (x,–y) = x – iy.
Contoh:
sekawan dari 3 + 2i adalah 3 – 2i , dan sekawan
dari 5i adalah –5i.
Operasi aljabar bilangan kompleks sekawan di dalam
himpunan bilangan kompleks memenuhi sifat-sifat
berikut :
11
z

12. Teorema 1 :
a. Jika z bilangan kompleks, maka :
1.
2.
3.
4.
12
[ ] [ ]22
)zIm()zRe(zz
)zIm(2zz
)zRe(2zz
zz
+=⋅
=−
=+
=

13. b. Jika z1
, z2
bilangan kompleks , maka :
1.
2.
3.
4. , dengan z2≠0.
13
2121 zzzz +=+
2121 zzzz −=−
2121 zzzz ⋅=⋅
2
1
2
1
z
z
z
z
=





2121 zzzz +=+
2121 zzzz −=−
2121 zzzz ⋅=⋅
2121 zzzz +=+
2121 zzzz −=−

14. Interpretasi Geometris Bilangan Kompleks
Karena z = x + iy dapat dinyatakan sebagai z= (x,y),
merupakan pasangan terurut bilangan real, maka z
dapat digambarkan secara geometri dalam koordinat
Kartesius sebagai sebuah titik (x,y). Pemberian nama
untuk sumbu x diubah menjadi sumbu Real dan
sumbu y diubah menjadi sumbu Imajiner. Bidang
kompleks tersebut di beri nama bidang Argand atau
bidang z. Jika kita hubungkan titik asal (0,0) dengan
titik (x,y), maka terbentuk vektor; sehingga bilangan
kompleks z = x+iy = (x,y) dapat dipandang sebagai
vektor z. Arti geometris dari penjumlahan dan
pengurangan bilangan kompleks dapat dilihat pada
gambar berikut.
14

15. 15
Re
Im
)y,x(z•
O
ArganBidang
z

16. 16
Im
Re
2z
1z
O
21 zz +

17. 17
Re
Im
2z
2z−
1z
21 zz −
O

18. Tugas :
Diketahui z1
= 2 + 3i dan z2
= 5 – i. Gambarkan pada
bidang kompleks (bidang argand), z1
,z2
, z1
+z2
, z1
-z2
,
18
⋅
212121 zz,zz,z,z −+

19. Modulus (Nilai Mutlak) dari Bilangan Kompleks
Definisi 4 :
Jika z = x+iy = (x,y) bilangan kompleks, maka
modulus dari z, ditulis |z| = |x+iy| =
Arti geometri dari modulus z adalah merupakan jarak
dari titik O(0,0) ke z = (x,y). Akibatnya, jarak antara
dua bilangan kompleks z1
=x1
+iy1
dan z2
= x2
+iy2
adalah
19
22
yx +
2
21
2
21 )yy()xx( −+−

20. Selanjutnya apabila z1
=x1
+iy1
dan r real positif,
maka |z – z1
| = r merupakan lingkaran yang berpusat di
titik z1
dengan jari-jari r.
Bagaimanakah dengan |z – z1
| < r dan |z – z1
| > r
Gambarkanlah pada bidang z.
20

21. Teorema 2 :
A. Jika z bilangan kompleks, maka berlaku :
1.
2.
3.
4.
5.
21
( ) ( )
)zIm()zIm(z
)zRe()zRe(z
zzz
zz
)zIm()zRe(z
2
222
≥≥
≥≥
⋅=
=
+=

22. B. Jika z1
, z2
bilangan kompleks, maka berlaku :
1.
2.
3.
4.
5.
Tugas : Buktikanlah teorema A di atas dengan
memisalkan z = x+iy, kemudian berdasarkan hasil A,
buktikan juga teorema B !
22
2121
2121
2121
2
1
2
1
2121
zzzz
zzzz
zzzz
z
z
z
z
zzzz
−≥−
−≥−
+≤+
=
⋅=⋅

23. 1. Bukti:
23
2121 zzzz ⋅=⋅
)iyx()iyx(zz 221121 +⋅+=⋅
)yxyx(i)yyxx( 12212121 ++−=
2121
2
1
2
2
2
2
2
12121
2
2
2
1
2
2
2
1 yyxx2yxyxyyxx2yyxx +++−+=
2
1221
2
2121 )yxyx()yyxx( ++−=
)yx()yx( 2
2
2
2
2
1
2
1 +⋅+=
)yx()yx( 2
2
2
2
2
1
2
1 +⋅+=
21 zz ⋅=
2121 zzzz ⋅=⋅∴

24. 2. Bukti:
24
22
22
22
11
2
1
iyx
iyx
iyx
iyx
z
z
−
−
⋅
+
+
=
2
2
2
2
2112
2
2
2
2
2121
yx
yxyx
i
yx
yyxx
+
−
+
+
+
=
2
2
2
2
2
2112
2
2
2
2
2
2121
yx
yxyx
yx
yyxx






+
−
+





+
+
=
22
2
2
2
2121
2
2
2
1
2
1
2
22121
2
2
2
1
2
2
2
1
)yx(
yyxx2yxyxyyxx2yyxx
+
−++++
=
)yx()yx(
)yx()yx(
2
2
2
2
2
2
2
2
2
2
2
2
2
1
2
1
+⋅+
+⋅+
=
.terbukti
z
z
yx
yx
2
1
2
2
2
2
2
1
2
1
=
+
+
=

25. 3. Bukti:
25
2121 zzzz +≤+
2
1221 )yxyx(0 −≤
2121
2
1
2
2
2
2
2
1 yyxx2yxyx0 −+≤
2
1
2
2
2
2
2
12121 yxyxyyxx2 +≤
2
1
2
2
2
2
2
1
2
2
2
1
2
2
2
12121
2
2
2
1
2
2
2
1 yxyxyyxxyyxx2yyxx +++≤++
)yx)(yx()yyxx( 2
2
2
2
2
1
2
1
2
2121 ++≤+
)yx)(yx(2)yyxx(2 2
2
2
2
2
1
2
12121 ++≤+
≤+++++ 2
221
2
1
2
221
2
1 yyy2yxxx2x
2
2
2
2
2
2
2
2
2
1
2
1
2
1
2
1 yx)yx)(yx(2yx ++++++
( )2
2
2
2
2
2
1
2
1
2
21
2
21 yxyx)yy()xx( +++≤+++
2
2
2
2
2
1
2
1
2
21
2
21 yxyx)yy()xx( +++≤+++
terbukti
zzzz 2121 +≤+

26. 4. Bukti:
26
2121 zzzz −≥−
2121
2121
221
2211
zzzz
zzzz
zzz
zzzz
−≥−∴
−≤−
+−≤
+−=

27. Bentuk Kutub (Polar) dan Eksponen dari
Bilangan
Kompleks
Selain dinyatakan dalam bentuk z = x+iy = (x,y),
bilangan kompleks z dapat dinyatakan pula dalam
bentuk koordinat kutub atau Polar, yaitu z = (r,θ).
27
O
θ
Im
Re
),r()y,x(z θ==
rz =

28. Adapun hubungan antara keduanya, dan
adalah :
x = r cosθ , y = r sinθ,
sehingga θ = arc tan
θ adalah sudut antara sumbu x positif dengan oz
didapat juga
Jadi, bentuk kutub bilangan kompleks z adalah
z = (r, θ) = r(cos θ + i sin θ) = r cis θ.
dan sekawan dari z adalah = (r, -θ) = r(cos θ - i sin
θ).
28






x
y
zyxr 22
=+=
)y,x( ),r( θ

29. Definisi 5 :
Pada bilangan kompleks z = (r, θ) = r(cos θ + i sin θ),
sudut θ disebut argument dari z, ditulis arg z. Sudut θ
dengan 0 ≤θ < 2π atau -π < θ ≤ π disebut argument
utama dari z, ditulis θ = Arg z. Pembatasan untuk
sudut θ tersebut dipakai salah satu saja.
Definisi 6 :
Dua bilangan kompleks z1
= r1
(cos θ1
+ i sin θ1
) dan z2
= r2
(cos θ2
+ i sin θ2
) dikatakan sama, jika r1
= r2
, dan θ1
= θ2
.
29

30. Selain penulisan bilangan kompleks z = (x , y) = (r, θ)
= r(cos θ + i sin θ) = r cis θ, maka anda dapat
menuliskan z dalam rumus Euler (eksponen), yaitu z
= reiθ
, dan sekawannya adalah re-iθ
.
Tugas: Buktikan bahwa eiθ
= cos θ + i sin θ, dengan
menggunakan deret MacLaurin untuk cos θ , sin θ
dan et
dengan mengganti t = iθ.
30

31. Contoh :
Nyatakan bilangan kompleks z = 1 + i dalam bentuk
polar dan eksponen !
31

32. Contoh :
Nyatakan bilangan kompleks z = 1 + i dalam bentuk
polar dan eksponen !
Jawab :
z = 1 + i, r = , tan θ = 1, sehingga θ = 45⁰= π
Jadi z = (cos π + i sin π) = cis π =
32
2 4
1
4
1
2 4
1 2
i
4e
π2 4
1

33. Pangkat dan Akar dari Bilangan Kompleks
Perkalian dan Pemangkatan
Telah kita ketahui bahwa bilangan kompleks dalam
bentuk kutub adalah z = r(cos θ + i sin θ).
Jika z1
= r1
(cos θ1
+ i sin θ1
) & z2
= r2
(cos θ2
+ i sin θ2
),
maka kita peroleh hasil perkalian keduanya sebagai
berikut :
z1
z2
= [r1
(cos θ1
+ i sin θ1
)][r2
(cos θ2
+ i sin θ2
)]
z1
z2
= r1
r2
[(cos θ1
cos θ2
- sinθ1
sin θ2
) +
i (sin θ1
cos θ2
+ cos θ1
sin θ2
)]
z1
z2
= r1
r2
[cos (θ1
+ θ2
) + i sin (θ1
+ θ2
)]
33

34. Dari hasil perkalian tersebut diperoleh:
arg(z1
z2
) = θ1
+ θ2
= arg z1
+ arg z2
Pertanyaan :
Bagaimanakah jika kita perkalikan z1
z2
. . . zn
dan
z z z z … z = zn
?
34

35. Jika diketahui:
z1
= r1
(cos θ1
+ i sin θ1
)
z2
= r2
(cos θ2
+ i sin θ2
)
zn
= rn
(cos θn
+ i sin θn
), untuk n asli,
maka secara induksi matematika, diperoleh rumus
perkalian z1
z2
… zn
= r1
r2
…rn
[cos (θ1
+ θ2
+…+θn
) + i sin
(θ1
+ θ2
+…+θn
)] .
Akibatnya jika, z = r(cos θ + i sin θ) maka
zn
= rn
(cos nθ + i sin nθ).
. . . . . . . . . .1
Khusus untuk r = 1, disebut Dalil De-Moivre
(cos θ + i sin θ)n
= cos nθ + i sin nθ, n asli.
35


36. Pembagian:
Sedangkan pembagian z1
dan z2
adalah sebagai
berikut:
Setelah pembilang dan penyebut dikalikan dengan
sekawan penyebut, yaitu r2(cos θ2
- i sin θ2
), maka
diperoleh : [cos (θ1
- θ2
) + i sin (θ1
- θ2
)]
Dari rumus di atas diperoleh:
arg θ1
-θ2
= arg z1
– arg z2.
36
)sini(cosr
)sini(cosr
z
z
222
111
2
1
θ+θ
θ+θ
=
2
1
2
1
r
r
z
z
=
=
2
1
z
z

37. Akibat lain jika z = r(cos θ + i sin θ),
maka:
Untuk: .
Setelah pembilang dan penyebut dikalikan sekawan
penyebut, maka didapat :
. . . . . . 2
37
( )
( )θ+θ
=
θ−+θ−=
nsinincosr
1
z
1
)sin(i)cos(
r
1
z
1
nn
( ))nsin(i)ncos(
r
1
z
1
nn
θ−+θ−=

38. Dari 1 dan 2 diperoleh:
, Dalil De-Moivre
berlaku untuk semua n bilangan bulat.
38
)nsin(i)ncos(rz nn
θ+θ=

39. Contoh:
Hitunglah :
Jawab :
Misalkan maka
karena z di kuadran IV, maka dipilih
jadi
maka
39
3
1tan
213zr
,i3z
−=θ
=+==
−=
( ) ( )
6
6
6
6
3 2 cos 180 sin 180
2 ( 1 0)
2
o o
i i
−
−
−
−
− = − + −
= − +
=−
o
30−=θ
( ) 6
i3
−
−
( )3 2 cos 30 sin 30o o
i i− = − + −

40. Akar Bilangan Kompleks
Bilangan kompleks z adalah akar pangkat n dari
bilangan kompleks w, jika zn
= w, dan ditulis .
Jika z = ρ(cosφ +i sinφ) akar pangkat n dari bilangan
kompleks w = r(cosθ+i sinθ), maka dari zn
= w
diperoleh: ρn
(cosnφ +i sinnφ) = r(cosθ+i sinθ),
sehingga ρn
= r dan nφ= θ+2kπ , k bulat.
Akibatnya dan
Jadi . . .
40
n
1
wz =
n
1
r=ρ n
k2 π+θ=φ

41. Jadi, akar pangkat n dari bilangan kompleks
w = r(cosθ+i sinθ) adalah:
z = [cos( ) + i sin ( )], k bulat dan n
bilangan asli.
Dari persamaan zn
= w, ada n buah akar berbeda
yang memenuhi persamaan itu.
Untuk mempermudah dipilih k = 0,1,2,3,…,(n-1);
0 ≤ < 2π, sehingga diperoleh z1
,z2
,z3
,…,zn
sebagai akar ke-n dari z.
41
n
k2 π+θ2k
n
θ π+
n
k2 π+θ

42. Contoh :
Hitunglah (-81)1/4
Jawab :
Misalkan z = (-81)1/4
, berarti harus dicari penyelesaian
persamaan z4
= -81.
Tulis z = ρ(cosφ +i sinφ) dan –81 = 81(cos1800
+i sin1800
),
sehingga ρ4
(cos4φ +i sin4φ) = 81(cos1800
+i sin1800
),
diperoleh ρ4
= 81, atau ρ = 3 dan .
Jadi z= 3[cos( )+i sin( )]
Keempat akar yang dicari dapat diperoleh dengan
mensubstitusi k = 0,1,2,3 ke persamaan terakhir.
42
4
k2 π+π=φ
4
k2 π+π
4
k2 π+π

43. Latihan Soal Bab I
1. Buktikan Teorema 1 dengan memisalkan
z = (x,y) = x + iy.
2. Diketahui z1
= 6 + 5i dan z2
= 8 – i.
Tentukan z1
+z2
, z1
-z2
,z1
z2
, dan z1
/ z2
3. Jika z = -1-i, buktikan z2
+ 2z + 2 = 0.
4. Cari bilangan kompleks z yang memenuhi
sifat: a. z-1
= z dan b.
5. Buktikan untuk setiap z bilangan kompleks
berlaku : z1
. + .z2
= 2Re(z1
. )
6. Hitung jarak antara z1
= 2 + 3i dan z2
= 5 – i.
43
zz −=
1z2z 2z

44. 7.Gambarkan pada diagram argand dan
sebutkan nama kurva yang terjadi :
a. |z – 5| = 6 dan |z – 5| > 6
b. |z + i| = |z – i|
c. 1 < |z – i| < 3
8.Nyatakan bilangan kompleks z = 2 -2i dalam
bentuk polar dan eksponen !
9. Hitunglah (-2+2i)15
10.Tentukan himpunan penyelesaian dari : z3
- i = 0
44

45. BAB II
FUNGSI , LIMIT DAN KEKONTINUAN
Sebelum dibahas mengenai fungsi kompleks,
maka perlu dipelajari konsep-konsep topologi yang
akan digunakan pada fungsi kompleks.
Konsep-Konsep Topologi Pada Fungsi
Kompleks
Himpunan pada pembahasan ini adalah koleksi atau
kumpulan titik-titik pada bidang Z. Dianggap anda
telah memahami operasi pada himpunan yaitu
gabungan, irisan, penjumlahan dan pengurangan
beserta sifat-sifatnya.
45

46. 1. Lingkungan/persekitaran
a. Persekitaran zo
adalah himpunan semua titik z yang
terletak di dalam lingkaran yang berpusat di zo
,
berjari-jari r, r > 0. Ditulis N(zo
,r) atau |z – zo
| < r.
b. Persekitaran tanpa zo
adalah himpunan semua titik
z≠zo
yang terletak di dalam lingkaran yang berpusat
di zo
, berjari-jari r, r > 0. Ditulis N*(zo
,r) atau
0< |z – zo
| < r.
46

47. Contoh :
a. N(i,1) atau |z – i | < 1, lihat pada gambar 1
b. N*(O,a) atau 0< |z – O| < a, lihat pada gambar 2
47
Im
Re
•i
i2•
O
1gambar
Re
Im
O
2gambar
a

48. 2. Komplemen
Andaikan S suatu himpunan. Komplemen dari S
ditulis Sc
,merupakan himpunan semua titik pada
bidang Z yang tidak termasuk di S.
Contoh :
Gambarkan !
A = { z | Im z< 1}, maka Ac
= { z | Im z≥ 1}.
B ={ z | 2<z<4}, maka Bc
= { z | z≤2 atau z≥4}.
48

49. A = { z | Im z< 1}, maka Ac
= { z | Im z≥ 1}.
B ={ z | 2<z<4}, maka Bc
= { z | z≤2 atau z≥4}.
49
Re
Im
O
1
A
Re
Im
O 2 4
4
2
B
c
A
c
B

50. 3. Titik limit
Titik zo disebut titik limit dari himpunan S jika untuk
setiap N*(zo,δ) maka N*(zo,δ) ∩ S ≠ φ. Jika zo ∈ S dan
zo bukan titik limit, maka zo disebut titik terasing.
50

51. 3. Titik limit
Titik zo disebut titik limit dari himpunan S jika untuk
setiap N*(zo,δ) maka N*(zo,δ) ∩ S ≠ φ. Jika zo ∈ S dan
zo bukan titik limit, maka zo disebut titik terasing.
4. Titik batas
Titik zo disebut titik batas dari himpunan S jika untuk
setiap N*(zo,δ) memuat suatu titik di S dan memuat
suatu titik yang tidak di S.
51

52. 3. Titik limit
Titik zo disebut titik limit dari himpunan S jika untuk
setiap N*(zo,δ) maka N*(zo,δ) ∩ S ≠ φ. Jika zo ∈ S dan
zo bukan titik limit, maka zo disebut titik terasing.
4. Titik batas
Titik zo disebut titik batas dari himpunan S jika untuk
setiap N*(zo,δ) memuat suatu titik di S dan memuat
suatu titik yang tidak di S.
5. Batas dari himpunan S
adalah himpunan semua titik batas dari S.
52

53. 6. Interior dan Eksterior
Titik zo disebut interior dari himpunan S jika ada
N(zo,δ) sehingga N(zo,δ) ⊂ S. Titik yang bukan titik
interior atau bukan titik batas disebut titik eksterior.
53

54. 6. Interior dan Eksterior
Titik zo disebut interior dari himpunan S jika ada
N(zo,δ) sehingga N(zo,δ) ⊂ S. Titik yang bukan titik
interior atau bukan titik batas disebut titik eksterior.
7. Himpunan Terbuka
Himpunan S disebut himpunan terbuka jika semua
anggota S adalah titik interior S.
54

55. 6. Interior dan Eksterior
Titik zo disebut interior dari himpunan S jika ada
N(zo,δ) sehingga N(zo,δ) ⊂ S. Titik yang bukan titik
interior atau bukan titik batas disebut titik eksterior.
7. Himpunan Terbuka
Himpunan S disebut himpunan terbuka jika semua
anggota S adalah titik interior S.
8. Himpunan Tertutup
Himpunan S disebut himpunan tertutup jika S
memuat semua titik limitnya.
55

56. 9. Himpunan Terhubung
Himpunan terbuka S disebut terhubung, jika setiap
dua titik di S dapat dihubungkan oleh penggal garis
yang seluruhnya terletak di S.
56

57. 9. Himpunan Terhubung
Himpunan terbuka S disebut terhubung, jika setiap
dua titik di S dapat dihubungkan oleh penggal garis
yang seluruhnya terletak di S.
10. Daerah domain
Himpunan terbuka S yang terhubung disebut daerah
domain.
57

58. 9. Himpunan Terhubung
Himpunan terbuka S disebut terhubung, jika setiap
dua titik di S dapat dihubungkan oleh penggal garis
yang seluruhnya terletak di S.
10. Daerah domain
Himpunan terbuka S yang terhubung disebut daerah
domain.
11. Daerah Tertutup
Daerah tertutup S adalah daerah terbuka digabung
dengan batasnya.
58

59. 12. Penutup dari himpunan S
adalah himpunan S digabung dengan titik limitnya.
59

60. Contoh :
1.Diberikan A = { z / |z|<1}, maka:
A adalah himpunan terbuka dan terhubung.
Batas dari A adalah { z / |z|=1}.
Penutup dari A adalah { z / |z|≤1}.
60
Im
Re
1
11−
1−
A

61. 2.Diberikan B = { z / |z|<1} U {(0,1)}, maka:
B adalah bukan himpunan terbuka dan juga bukan
himpunan tertutup.
Titik-titik limit dari B adalah { z / |z|≤1}.
61
Im
Re
1
11−
1−
•
B

62. 3.Diberikan C = { z / |z|≤ 2}, maka:
Titik-titik interior C adalah { z / |z|<2}.
62
Im
Re
1
11−
1−
2
22−
2−

63. Fungsi Kompleks
Definisi :
Misalkan D himpunan titik pada bidang Z.
Fungsi kompleks f adalah suatu aturan yang
memasangkan setiap titik z anggota D dengan satu dan
hanya satu titik w pada bidang W, yaitu (z,w).
Fungsi tersebut ditulis w = f(z).
Himpunan D disebut daerah asal (domain) dari f, ditulis
Df
dan f(z) disebut nilai dari f atau peta dari z oleh f.
Range atau daerah hasil (jelajah) dari f ditulis Rf
, yaitu
himpunan f(z) untuk setiap z anggota D.
63

64. 64
z )z(fw =
)zRe( )wRe(
)zIm( )wIm(
Bidang Z Bidang W
f

65. Contoh :
a) w = z + 1 – i
b) w = 4 + 2i
c) w = z2
– 5z
d) f(z) =
Contoh a,b,c adalah fungsi kompleks dengan domain
semua titik pada bidang Z.
Contoh d adalah fungsi kompleks dengan domain
semua titik pada bidang Z , kecuali z =
65
1z2
z3
+
−
2
1−

66. Jika z = x + iy, maka fungsi w = f(z) dapat diuraikan
menjadi w = u(x,y) + iv(x,y) yang berarti Re(w) dan Im(w)
masing-masing merupakan fungsi dengan dua variabel
real x dan y.
Apabila z = r(cosθ + i sinθ), maka w = u(r, θ) + iv(r, θ).
66

67. Contoh :
Tuliskan f(z) = 2z2
– i dalam bentuk u dan v !
67

68. Contoh :
Tuliskan f(z) = 2z2
– i dalam bentuk u dan v !
Jawab :
Misal z = x + iy,
maka fungsi w = f(z) = 2z2
– i
= 2(x + iy )2
– i
= 2(x2
+2xyi-y2
) – i
= 2(x2
-y2
) + i(2xy-1).
Jadi u = 2(x2
-y2
) dan v = 2xy-1.
68

69. Jika z = r(cosθ + i sinθ).
Tentukan f(z) = z2
+ i
69

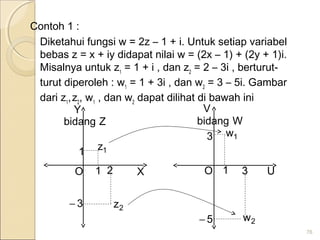
70. Jika z = r(cosθ + i sinθ).
Tentukan f(z) = z2
+ i
Jawab
f(z) = z2
+ i
= [r (cosθ+i sinθ)]2
+ i
= r2
[cos2
θ - sin2
θ + 2isinθcosθ] + i
= r2
(cos2
θ - sin2
θ) + r2
isin2θ + i
= r2
(cos2
θ - sin2
θ) +(1+r2
sin2θ)i
berarti u = r2
(cos2θ - sin2
θ) dan v = 1+r2
sin2θ) .
70

71. Komposisi Fungsi
Diberikan fungsi f(z) dengan domain Df
dan fungsi
g(z) dengan domain Dg
.
‣ Jika Rf
∩ Dg
≠ φ, maka ada fungsi komposisi (g⃘f) (z)
= g (f (z)), dengan domain Df
.
71
f g
fg 
z )z(f
( )
)z)(fg(
)z(fg

=

72. ‣ Jika Rg
∩ Df
≠ φ, maka ada fungsi komposisi (f⃘g) (z)
= f (g (z)), dengan domain Dg
.
∷ Tidak berlaku hukum komutatif pada (g⃘f) (z) dan
(f⃘g)(z).
72
g f
gf 
z )z(g
( )
)z)(gf(
)z(gf

=

73. Contoh :
Misal:f(z) = 3z – i dan g(z) = z2
+ z –1 + i
‣ Jika Rf
∩ Dg
≠ φ,
maka (g⃘f) (z) = g (f (z))
= g(3z – i)
= (3z – i)2
+ (3z – i) –1 + i
= 9z2
– 6iz – 1 + 3z – i – 1 + i
= 9z2
– 3z – 2 – 6iz
73

74. ‣ Jika Rg
∩ Df
≠ φ,
maka (f⃘g) (z) = f (g (z))
= f(z2
+ z –1 + i)
= 3z2
+ 3z – 3 + 3i – i
Karena 9z2
– 3z – 2 – 6iz ≠ 3z2
+ 3z – 3 + 3i – i
Jadi (g⃘f) (z) ≠ (f⃘g)(z) atau
(g⃘f) ≠ (f⃘g), (tidak komutatif)
74

75. Interpretasi Geometris
Untuk setiap variabel bebas z = x + iy anggota
domain ada satu dan hanya satu variabel tak bebas
w = u + iv yang terletak pada suatu bidang kompleks.
Masing-masing variabel terletak pada suatu bidang
kompleks, z pada bidang Z dan w pada bidang W.
Karena pasangan (z,w) mengandung 4 dimensi,
maka kita tidak dapat menggambarkannya pada satu
sistem. Tetapi kita dapat melihat gambaran dari w =
f(z). Caranya dengan memandang fungsi f tersebut
sebagai pemetaan (transformasi) dari titik di bidang Z
ke titik di bidang W dengan aturan f. Untuk suatu titik
z maka f(z) disebut peta dari z.
75

76. Contoh 1 :
Diketahui fungsi w = 2z – 1 + i. Untuk setiap variabel
bebas z = x + iy didapat nilai w = (2x – 1) + (2y + 1)i.
Misalnya untuk z1
= 1 + i , dan z2
= 2 – 3i , berturut-
turut diperoleh : w1
= 1 + 3i , dan w2
= 3 – 5i. Gambar
dari z1
,z2
, w1
, dan w2
dapat dilihat di bawah ini
76
X U
Y V
1z
2z
1w
2w
O O
Zbidang Wbidang
1
1
2
3−
1
3
3
5−

77. Contoh 2 :
Diketahui fungsi w = z2
.
Dengan menggunakan z = r (cosθ+i sinθ), maka
diperoleh w = z2
= r2
(cos2θ+i sin2θ).
Jika sebuah lingkaran pusat O berjari-jari r pada
bidang Z, maka dapat dipetakan ke bidang W
menjadi sebuah lingkaran pusat O berjari-jari r2
.
Daerah 0 ≤ arg z ≤ α dipetakan menjadi daerah
0 ≤ arg w ≤ 2α.
Gambar keduanya dapat dilihat di bawah ini.
77

78. 78
α α2
Zbidang
Wbidang
r
2
r

79. 79
Diketahui daerah D pada bidang
Z dan titik zo terletak di dalam D
atau pada batas D. Misalkan
fungsi w = f(z) terdefinisi pada D,
kecuali di zo.
•
oz
D z
),z(*N o δ
δ
Apabila titik z bergerak mendekati
titik zo melalui setiap lengkungan
sebarang K dan mengakibatkan
nilai f(z) bergerak mendekati
suatu nilai tertentu, yaitu wo pada
bidang W, maka dikatakan limit
f(z) adalah wo untuk z mendekati
zo, ditulis :
)z(f•
),w(N o ε
ε
o
zz
w)z(flim
o
=
→
Limi
t

•
ow
D
K
Zbidang
Wbidang

80. Definisi :
Misalkan fungsi w = f(z) terdefinisi pada daerah D,
kecuali di zo
(titik zo
di dalam D atau pada batas D).
limit f(z) adalah wo
untuk z mendekati zo
, jika untuk
setiap ε > 0, terdapat δ > 0 sedemikian hingga
|f(z) – wo
|< ε, apabila 0 <|z – zo
|< δ,
ditulis:
80
o
zz
w)z(flim
o
=
→

81. Perlu diperhatikan bahwa :
1. Titik zo
adalah titik limit domain fungsi f.
2. Titik z menuju zo
melalui sebarang lengkungan K,
artinya z menuju zo
dari segala arah.
3. Apabila z menuju zo
melalui dua lengkungan yang
berbeda, mengakibatkan f(z) menuju dua nilai yang
berbeda, maka limit fungsi f tersebut tidak ada
untuk z mendekati zo
.
81

82. 82
Contoh 1 :
Buktikan bahwa : 5
2z
2z3z2
lim
2
2z
=
−
−−
→

83. Contoh 1 :
Buktikan bahwa :
Bukti:
Misalkan diberikan bilangan ε > 0, kita akan mencari
δ > 0 sedemikian, sehingga:
, untuk z ≠ 2
Lihat bagian sebelah kanan
83
ε<−
−
−−⇒δ<−< |5
2z
2z3z2||2z|0
2
5
2z
2z3z2
lim
2
2z
=
−
−−
→

84. Dari persamaan kanan diperoleh:
Hal ini menunjukkan bahwa telah diperoleh.
84
2
|2z|
|)2z(2|
|
)2z(
)2z)(51z2(
|
|5
)2z(
)2z)(1z2(
||5
2z
2z3z2|
2
ε<−⇔
ε<−⇔
ε<
−
−−+
⇔
ε<−
−
−+
⇔ε<−
−
−−
2
ε=δ

85. Bukti Formal :
Jika diberikan ε > 0 , maka terdapat , sehingga
untuk z ≠ 2, diperoleh
Jadi apabila
Terbukti
85
ε=δ<−=
−
−
−+
=
−
−
−−⇒δ<−<
2|)2z(2|
|5
)2z(
)2z)(1z2(
|
|5
2z
2z32z2||2z|0
2
ε=δ
ε<−
−
−− |5
2z
2z32z2|
2
|2z|0 ε=δ<−<
5
2z
2z3z2lim
2
2z
=
−
−−
→

86. Teorema Limit :
Teorema 1 :
Jika fungsi f mempunyai limit untuk z menuju zo
,
maka nilai limitnya tunggal.
86

87. Teorema Limit :
Teorema 1 :
Jika fungsi f mempunyai limit untuk z menuju zo
,
maka nilai limitnya tunggal.
Bukti:
Misal limitnya w1 dan w2, maka
87
21
21
2121
2
11
wwjadi
wwsehingga
22
w)z(f)z(fww)z(f)z(fw
2
w)z(f
2
)z(fww)z(f
=
ε≤−
ε=ε+ε=−+−≤−+−
ε=−
ε=−=−

88. Teorema 2 :
Misalkan z = (x,y) = x+iy dan f(z) = u(x,y) + iv(x,y)
dengan domain D. Titik zo
= (xo
,yo
) = xo
+iyo
di dalam D
atau batas D.
Maka jika dan hanya jika
dan
88
oo
zz
iyx)z(flim
o
+=
→
o
zz
x)y,x(ulim
o
=
→
o
zz
y)y,x(vlim
o
=
→

89. Teorema 3 :
Misalkan fungsi f dan g limitnya ada.
lim f(z) = a dan lim g(z) = b, maka
1. lim (f(z) +g(z)) = a + b (untuk z → zo
)
2. lim (f(z) . g(z)) = a . b (untuk z → zo
)
3. lim (f(z) / g(z)) = a / b (untuk z → zo
)
Tugas : Buktikan ketiga teorema limit tersebut !
89

90. Contoh 1 :
Hitunglah
90
iz
1z
lim
2
iz −
+
→

91. Contoh 1 :
Hitunglah
Jawab:
91
iz
1z
lim
2
iz −
+
→
i2
)iz(lim
iz
)iz)(iz(
lim
iz
1zlim
iz
iz
2
iz
=
+=
−
−+
=
−
+
→
→→

92. Contoh 2 :
Jika . Buktikan tidak ada !
92
i
1y
x
yx
xy2
)z(f
2
22 +
+
+
= )z(flim
0z→

93. 93
Contoh 2 :
Jika . Buktikan tidak ada !i
1y
x
yx
xy2
)z(f
2
22 +
+
+
= )z(flim
0z→
Bukti :
Kita tunjukkan bahwa untuk z menuju 0 di sepanjang
garis y = 0, maka
Sedangkan di sepanjang garis y = x,
Dari 1 dan 2, terbukti tidak ada
10ixlim)z(flim)z(flim 2
0x)0,0()0,x(0z
===
→→→
21)i
1x
x1(lim)z(flim)z(flim
2
0x)0,0()x,x(0z
=
+
+==
→→→
)z(flim
0z→

94. Kekontinuan Fungsi
Definisi :
Misalkan fungsi f(z) terdefinisi di D pada bidang Z
dan titik zo
terletak pada interior D, fungsi f(z)
dikatakan kontinu di zo
jika untuk z menuju zo
,
maka lim f(z) = f(zo
).
94

95. Jadi, ada tiga syarat fungsi f(z) kontinu di zo
, yaitu :
Fungsi f(z) dikatakan kontinu pada suatu daerah R,
jika f(z) kontinu pada setiap titik pada daerah R
tersebut.
95
)z(f)z(flim.3
ada)z(flim.2
ada)z(f.1
o
zz
zz
o
o
o
=
→
→

96. Teorema 4 :
Jika f(z) = u(x,y) + iv(x,y), f(z) terdefinisi di setiap titik
pada daerah R, dan zo
= xo
+ i yo
titik di dalam R, maka
fungsi f(z) kontinu di zo
jika dan hanya jika u(x,y) dan
v(x,y) masing-masing kontinu di (xo
,yo
).
96

97. Teorema 5 :
Andaikan f(z) dan g(z) kontinu di zo
, maka masing-
masing fungsi :
1. f(z) + g(z)
2. f(z) . g(z)
3. f(z) / g(z), g(z) ≠ 0
4. f(g(z)); f kontinu di g(zo
),
kontinu di zo
.
97

98. 98
Contoh 1 :
Fungsi f(z) = , apakah kontinu di 2i
Jawab :
f(2i) = 3 + 4(2i) = 3 + 8i,
sedangkan untuk z mendekati 2i, lim f(z) = z + 2i,
jadi f(z) diskontinu di z = 2i.







=+
≠
−
+
i2z,z43
i2z,
i2z
4z2
)i2(f)z(flimsehingga
i2z
≠
→

99. 99
Contoh 2.
Dimanakah fungsi kontinu ?
Jawab :
Coba anda periksa bahwa g(z) diskontinu di z = 1 dan
z = 2. Jadi g(z) kontinu di daerah
2z3z
1z)z(g 2
2
+−
+=
{ }2zz >

100. BAB III. TURUNAN
3.1 Definisi Turunan
Diberikan fungsi f yang didefinisikan pada daerah D dan
zo
∈ D.
Jika diketahui bahwa nilai ada, maka
nilai limit ini dinamakan turunan atau derivatif fungsi f di
titik zo
.
Dinotasikan : f’(zo
)
100
o
o
zz zz
)z(f)z(f
lim
o
−
−
→

101. ⇛ Jika f’(zo
) ada, maka f dikatakan terdifferensial atau
diferensiabel di zo
.
Dengan kata lain :
⇛ Jika f terdifferensial di semua titik pada D, maka f
terdifferensial pada D
Contoh 3.1.1
Buktikan f(z) = z2
terdifferensiasi diseluruh ℂ
101
z
)z(f)zz(f
lim
z
flim)z('f oo
0z0z
o ∆
−∆+
=
∆
∆=
→∆→∆

102. Bukti :
Ditinjau sebarang titik zo
∈ ℂ
102
o
o
oo
zz
o
2
o
2
zz
o
o
zz
o
z2
zz
)zz)(zz(
lim
zz
zz
lim
zz
)z(f)z(f
lim)z('f
o
o
o
=
−
−+
=
−
−
=
→
−
=
→
→
→
Karena zo sebarang maka f(z) = z2
terdefferensial
di seluruh ℂ

103. Teorema 3.1
Jika f fungsi kompleks dan f’(zo
) ada, maka
f kontinu di zo
Bukti :
103

104. Bukti :
Diketahui f’(zo
) ada
Akan dibuktikan f kontinu di zo
atau
104
)z(f)z(flim o
zz o
=
→
0
0)z('f
)zz(lim
)zz(
)z(f)z(f
lim
)zz(
)zz(
)z(f)z(f
lim))z(f)z(f(lim
o
zzo
o
zz
o
o
o
zz
o
zz
oo
oo
=
⋅=
−⋅
−
−
=





 −⋅
−
−
=−
→→
→→
sehingga
dengan kata lain f kontinu di zo.
)z(f)z(flim)z(flim oo
zzzz oo
==
→→

105. Contoh 3.1.2
Buktikan f(z) = |z|2
kontinu di seluruh bidang kompleks
tetapi hanya terdifferensial di z = 0
Bukti :
f(z) = |z|2
= x2
+ y2
berarti u(x,y) = x2
+ y2
dan
v(x,y) = 0
u dan v kontinu di D, maka f(z) kontinu di D
105
0
z
zzlim
z
|z|
lim
0z
)0(f)z(f
lim)0('f
0z
2
0z0z
==
=
−
−
=
→
→→
Jadi f(z) terdifferensial di z = 0

106. 106
3.2 Syarat Chauchy-Riemann
Syarat yang diperlukan agar fungsi f terdiferensial di
zo = xo + i yo adalah syarat Chauchy-Riemann, yang
menghubungkan derivatif-derivatif parsial tingkat pertama
dari fungsi bagian real dan fungsi bagian imajiner dari f.

107. 107
Terema 3.2.1 (Syarat Chauchy-Riemann
Jika f(z) = u(x,y) + i v(x,y) terdifferensial di zo = xo + i yo,
maka u(x,y) dan v(x,y) mempunyai derivatif parsial
pertama di (xo,yo) dan di titik ini dipenuhi persamaan
Cauchy – Riemann
derivatif f di zo dapat dinyatakan dengan
Jika persamaan C-R tidak dipenuhi di (xo,yo) maka
f(z) = u(x,y) + i v(x,y) tidak terdifferensial di zo = xo + i yo
x
v
y
udan
y
v
x
u
∂
∂−=
∂
∂
∂
∂=
∂
∂
)y,x(vi)y,x(u)z('f ooxooxo +=

108. 108
Contoh 3.2.1
Buktikan f(z) = |z|2
tidak terdifferensiasi di z ≠ 0
Bukti : f(z) = x2
+ y2
sehingga
u(x,y) = x2
+ y2
v(x,y) = 0
Persamaan Cauchy – Riemann
y2
y
udanx2
x
u =
∂
∂=
∂
∂
0
y
vdan0
x
v =
∂
∂=
∂
∂
)1(0x2
y
v
x
u =⇔
∂
∂=
∂
∂

109. 109
)2(0y2
x
v
y
udan =⇔
∂
∂−=
∂
∂
(1) dan (2) tidak dipenuhi jika x ≠ 0 atau y ≠ 0,
jadi pasti f tidak terdeferensial di z ≠ 0

110. 110
Catatan :
Syarat C-R hanya syarat perlu untuk keterdifferensialan.
Contoh 3.2.2
Buktikan fungsi f(z) = 22
33
yx
i)1(yi)1(x
+
−−+
dan f(0) = 0, tidak terdifferensial di 0, memenuhi C-R
Bukti :
u = 22
33
yx
yx
+
−
dengan u(0,0) = 0
v = 22
33
yx
yx
+
+
dengan v(0,0) = 0
ux
(0,0) =
ox
lim
→ x
)0,0u()0u(x, −
= 1
uy
(0,0) = y
)0,0u(,y)0u(
lim
oy
−
→
= -1

111. 111
vx
(0,0) =
x
)0,0v()0v(x,
lim
ox
−
→
= 1
oy
lim
→ y
)0,0v(,y)0v( −
vy
(0,0) = = 1
Jadi persamaan Cauchy – Riemann terpenuhi
iy))(xy(x
i)1(yi)1(x
lim
z
)0(f)z(f
lim 22
33
0z0z ++
−−+
=
−
→→
Tetapi
Untuk z → 0
ox
lim
→ 3
3
x
i)1(x +
Sepanjang garis real y = 0 → = 1 + i

112. 112
ox
lim
→ 3
3
xi)1(2
xi2
+ i1
i
+Sepanjang garis real y = x → =
oz
lim
→ z
)0f(f(z) −Jadi tidak ada
sehingga f tidak terdifferensial di 0 meskipun
persamaan C-R dipenuhi di (0,0)

113. 113
x
u
∂
∂
y
u
∂
∂
x
v
∂
∂
y
v
∂
∂
x
u
∂
∂
y
v
∂
∂
y
u
∂
∂
x
v
∂
∂−
Dengan demikian dapat disimpulkan bahwa :
i. Syarat perlu
f(z) = u(x,y) + iv(x,y), zo
= xo
+ i yo
f’(z) ada maka ,, ,
berlaku C-R yaitu :
= dan =
dan f’(z0
) = ux
(x0
,y0
) + i vx
(x0
,y0
)
ada di (xo, yo)

114. 114
ii. Syarat cukup
u(x,y), v(x,y), ux(x,y), vx(x,y), uy(x,y), vy(x,y) kontinu
pada kitar zo = xo + i yo dan di (xo,yo) dipenuhi C-R
maka f’(zo) ada

115. 115
Contoh 3.2.3
Buktikan f(z) = ex
(cos y + i sin y) terdiferensial
untuk setiap z dalam ℂ
Bukti :
u(x,y) = ex
cos y → ux
(x,y) = ex
cos y
uy
(x,y) = -ex
sin y
v(x,y) = ex
sin y → vx
(x,y) = ex
sin y
vy
(x,y) = ex
cos y
ada dan
kontinu di
setiap (x,y) ∈ ℂ

116. 116
Berdasarkan persamaan C-R :
ux = vy dan uy = -vx dipenuhi di ∀ (x,y) ∈ ℂ, dan ada kitar
dimana keenam fungsi kontinu dan C-R dipenuhi di (x,y).
Jadi f’(z) ada ∀ z ∈ ℂ.
Dan f’(z) = ux(x,y) + i vx(x,y)
= ex
cos y + i ex
sin y

117. 117
3.3 Syarat C-R Pada Koordinat Kutub
Jika f(z) = u(x,y) + i v(x,y) dapat diilustrasikan
dalam koordinat kartesius maka dengan menggunakan
hubungan x = r cos ϕ dan y = r sin ϕ , diperoleh
z = r cos ϕ + i sin ϕ , sehingga
f(z) = u(r, ϕ) + i v(r, ϕ) dalam sistem koordinat kutub

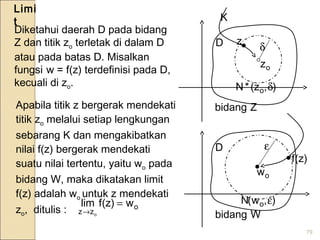
118. 118
Teoreama 3.3.1
Jika f(z) = u(r, ϕ) + i v(r, ϕ) terdiferensial dan kontinu
pada suatu kitar (ro, ϕo) dan jika dalam kitar tersebut
ur, uϕ, vr, vϕ ada dan kontinu di (ro, ϕo) dan dipenuhi
C-R yaitu:
r
u
∂
∂
r
1
ϕ∂
∂v
r
1
ϕ∂
∂v
r
v
∂
∂−= dan = , r ≠ 0
maka f’(z) = ada di z = zo dan
f’(z) = (cos ϕo – i sin ϕo) [ur(ro, ϕo) + i vr(ro, ϕo)]

119. 119
Contoh 3.3.1
Diketahui f(z) = z-3
,
tentukan f’(z) dalam bentuk kootdinat kutub

120. 120
Jawab :
f(z) = z-3
= r-3
(cos 3ϕ - i sin 3ϕ), maka :
u = r-3
cos 3ϕ , sehingga ur = -3r-4
cos 3ϕ dan
uϕ = -3r-3
sin 3ϕ
v = -r-3
sin 3ϕ , sehingga vr = 3r-4
sin 3ϕ dan
vϕ = -3r-3
cos 3ϕ
keenam fungsi ini kontinu dan syarat C-R dipenuhi
untuk semua z ≠ 0
Jadi f(z) = z-3
terdiferensial untuk z ≠ 0
Dengan demikian f’(z) dalam koordinat kutub adalah :
f’(z) = (cos ϕ – i sin ϕ) (-3r-4
cos 3ϕ + i 3r-4
sin 3ϕ)
= cis(-ϕ) (-3r-4
) cis(-3ϕ)
= -3r-4
cis(-4ϕ)

121. 121
[ ]
[ ]
[ ]
[ ]2
)z(g
)z('g)z(f)z(g)z('f
)z(g
)z(f
dx
d.5
)z('g)z(f)z(g)z('f)z(g)z(f
dx
d.4
)z('g)z('f)z(g)z(f
dx
d.3
)z('cf
dz
)z(cfd
.2
1
dz
d(z)
,0
dz
dc.1
−
=





+=
±=±
=
==
3.4 Aturan Pendiferensialan
Jika f(z), g(z) dan h(z) adalah fungsi- fungsi kompleks
serta f’(z), g’(z) dan h’(z) ada, maka berlaku rumus-rumus :

122. 122
dz
d
.
d
dw
dz
dw
)rantaiaturan(komposisidengandisebutbiasa
)z('f)]z(f['g)z('hmaka)]z(f[g)z(hJika.7
nz
dz
dz.6 1n
n
ϕ
ϕ
=
==
= −

123. 123
3.5 Fungsi Analitik
Definisi 3.5.1
Fungsi f analitik di zo, jika ada r > 0 sedemikian,
hingga f’(z) ada untuk setiap z ∈ N(zo,r)
(persekitaran zo)
r
f diferensiable
Fungsi analitik untuk setiap z∈ℂ dinamakan fungsi utuh
oz

124. 124
Contoh 3.5.1
1. f(z) =
2. f(z) = x3
+ iy3
diperoleh : u = x3
; v = y3
sehingga
ux = 3x2
; vx = 0 ; uy = 0 ; vy = 3y2
dengan menggunakan persamaan C-R :
3x2
= 3y2
⇒ y = ± x dan vx = uy = 0
persamaan C-R dipenuhi dan kontinu digaris y = ± x
berarti f’(z) ada hanya di y = ± x
Jadi f(z) tidak analitik dimanapun karena tidak ada
kitar.
z
1
analitik kecuali di z = 0

125. 125
( )
( )
( )
( )
0)z('g0)z(gdengan,
zg'
zf'
zg
zf
lim
ozz
≠≠=
→
Sifat sifat analitik
Misalnya f dan g analitik pada D, maka :
o f ± g merupakan fungsi analitik
o fg merupakan fungsi analitik
o f/g merupakan fungsi analitik dengan g ≠ 0
o h = g ∘ f merupakan fungsi analitik
o berlaku aturan L’hospital yaitu :

126. 126
3.6 Titik Singular
Definisi 3.6.1
Titik z1 disebut titik singular dari f jika f tidak analitik di z1
tetapi untuk setiap kitar dari z1 memuat paling sedikit
satu titik dimana f analitik.

127. 127
Jenis kesingularan f(z) atau titik singular antara lain :
1. Titik singular terisolasi
Titik zo dinamakan titik singular terisolasi dari f(z)
jika
terdapat δ > 0 demikian sehingga lingkaran |z – zo| = δ
hanya melingkari titik singular lainnya. Jika δ seperti itu
tidak ada, maka z = zo disebut titik singular tidak
terisolasi.

128. 128
2. Titik Pole (titik kutub)
Titik z = zo disebut titik pole tingkat n, jika berlaku
.
Jika n = 1, zo disebut sebagai titik pole sederhana.
3. Titik Cabang
Dari fungsi bernilai banyak dapat menjadi titik singular.
4. Titik Singular dapat dihapuskan
Titik singular zo disebut titik singular dapat
dihapuskan
dari f(z) jika f(z) ada.
0A)z(f)zz(lim n
o
zz o
≠=−
→
oz
lim
→

129. 129
5. Titik Singular Essensial
Titik singular z = zo yang tidak memenuhi syarat titik
singular pole titik cabang atau titik singular yang dapat
dihapuskan disebut titik singular essensial.
6. Titik Singular tak hingga
Jika f(z) mempunyai titik singular di z = ∞, maka sama
dengan menyatakan f(1/w) mempunyai titik singular di
w = 0.

130. 130
Contoh 3.6.1
• g(z) = berarti titik z = i adalah titik pole tingkat 2
dari g(z)
• h(z) = |z|2
tidak merupakan titik singular
• k(z) = ln (z2
+ z – 2) maka titik cabang adalah z1 = 1 dan
z2 = –2 karena (z2
+ z – 2) = (z – 1) (z + 2) = 0
2
)1z(
1
−

131. 131
3.7 Fungsi Harmonik
f(z) = u(x,y) + iv(x,y) analitik pada D maka u dan v
mempunyai derivatif parsial di semua orde yang
kontinue pada D. Jadi dalam D berlaku C-R , ux = vy dan
uy = –vx
Karena derifatif-derivatif parsial dari u dan v kontinue
dalam D, maka berlaku vxy = vyx. Jika dalam ux = vy dan
uy = –vx diderivatifkan parsial terhadap x dan y maka
∀(x,y) ∈D berlaku
uxx + uyy = 0
vxx = vyy = 0

132. 132
Jika f analitik pada D maka u dan v pada D memenuhi
persamaan differensial Laplace dalam 2 dimensi.
u dan v dimana f(z) = u(x,y) + iv(x,y) analitik pada suatu
domain maka f(z) harmonik pada domain tersebut.
Dua fungsi u dan v sedemikian sehingga
f(z) = u(x,y) + iv(x,y) analitik dalam suatu domain
dinamakan dua fungsi yang harmonik konjugat
dalam domain itu.
0
yx 2
2
2
2
=
∂
ϕ∂
+
∂
ϕ∂

133. 133
Contoh 3.7.1
Diberikan u(x,y) harmonik pada D dan tentukan fungsi v
yang harmonik konjugat dengan u = 4xy3
– 12x3
y, (x,y) ∈ℂ
Jawab :
Misal diklaim konjugatnya adalah v(x,y)
jadi f(z) = u(x,y) + iv(x,y) analitik pada ℂ sedemikian
sehingga berlaku C-R ux = vy dan uy = -vx
ux = 4y3
– 12x2
y vy = 4y3
– 12x2
y
uy= 12xy2
– 4x3
v= y4
– 6x2
y2
+ g(x)
karena vx = –uy maka –12xy2
+ g’(x) = –12xy2
+ 4x3
sehingga g’(x) = 4x3
diperoleh g(x) = x4
+ C
Jadi v = y4
– 6x2
y2
+ x4
+ C

134. 134
Cara Milne Thomson
Cara yang lebih praktis menentukan fungsi harmonik
konjugat atau dari fungsi harmonik u diberikan u(x,y)
harmonik pada D andaikan v(x,y) sehingga
f(z) = u(x,y)+ iv(x,y) analitik pada D
f”(z) = ux(x,y) + ivx(x,y)
sesuai persamaan C-R : f”(z) = ux(x,y) – iuy(x,y)
z = x + iy dan = x – iy sehingga diperoleh
z
i2
zzydan
2
zzx −=+=





 −+
i2
zz,
2
zz





 −+
i2
zz
,
2
zzf(z) = ux – iuy

135. 135
Suatu identitas dalam z dan , jika diambil = z maka
f’(z) = ux(z,0) – iuy(z,0)
Jadi f(z) adalah fungsi yang derivatifnya ux(z,0) – iuy(z,0)
kemudian didapat v(x,y)
z z

136. 136
Contoh 3.7.2
Dari Contoh 3.7.1 dengan u= 4xy3 – 4x3y, (x,y) ∈ ℂ,
jika diselesaikan dengan menggunakan cara Milne
Thomson.
Jawab :
ux = 4y3
– 12x2
y
uy= 12xy2
– 4x3
f’(z) = ux(z,0) – iuy(z,0)
= –i(– 4z3
)
= 4iz3
sehingga f(z) = iz4
+ A
f(z) = i(x + iy)4
+ A
= 4xy3
– 4x3
y + i(x4
– 6x2
y2
+ y4
) + A