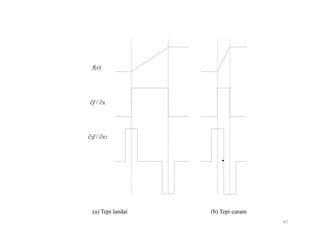
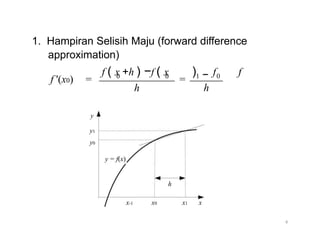
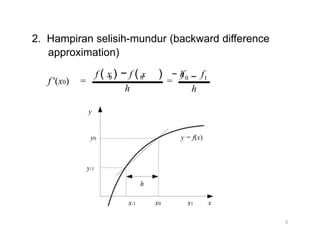
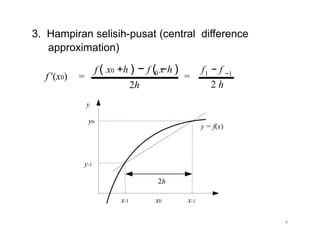
Dokumen ini membahas turunan numerik, termasuk definisi, pendekatan untuk menghitung turunan (selisih maju, mundur, dan pusat), serta bagaimana merumuskan turunan pertama dan kedua menggunakan deret Taylor dan polinom interpolasi. Beragam rumus disajikan untuk menghitung turunan dengan pendekatan yang berbeda, dicontohkan melalui analisis data tabel. Contoh konkret diberikan untuk menghitung nilai turunan pada titik tertentu dengan berbagai orde akurasi.

1. Turunan Numerik
Nama Kelompok :
Bobby Chandra A
1

2. Definisi Turunan (derivatif)
f '(x) =
lim f ( x+h ) − fx)
h → 0 h
• Bila persamaan fungsi f(x) diberikan secara eksplisit, maka kita
dapat menentukan fungsi turunannya, f '(x), f "(x), ..., f (n+1)(x), lalu
menggunakannya untuk menghitung nilai turunan fungsi di x = t.
• Tetapi jika fungsi f(x) tidak diketahui secara eksplisit, tetapi kita
hanya memiliki beberapa titik data saja. Pada kasus seperti ini kita
tidak dapat menemukan nilai turunan fungsi secara analitik.
• Sebaliknya, pada kasus lain, meskipun f(x) diketahui secara eksplisit
tetapi bentuknya rumit sehingga menentukan fungsi turunannya
merupakan pekerjaan yang tidak mangkus
2

3. Persoalan Turunan Numerik
• Persoalan turunan numerik ialah menentukan
hampiran nilai turunan fungsi f yang diberikan dalam
bentuk tabel.
• Tiga pendekatan dalam menghitung turunan
numerik:
1. Hampiran selisih maju
2. Hampiran selisih mundur
3. Hampiran selisih pusat
3

4. 1. Hampiran Selisih Maju (forward difference
approximation)
f ( x +h ) −f ( x ) f f
f '(x0) =
y
y1
y0
0 0
h
y = f(x)
h
1 − 0
=
h
x-1 x0 x1 x
4

5. 2. Hampiran selisih-mundur (backward difference
approximation)
f
f '(x0) =
y
y0
y-1
( x0 ) − f ( x − h0
h
h
) f f0 − 1
=
h
y = f(x)
x-1 x0 x1 x
5

6. 3. Hampiran selisih-pusat (central difference
approximation)
f
f '(x0) =
y
y0
y-1
( x0 +h ) − f ( x
2h
0 −h ) f − f1 −1
=
2 h
y = f(x)
2h
x-1 x0 x-1
6

7. • Rumus-rumus turunan numerik untuk ketiga
pendekatan tersebut dapat diturunkan dengan dua
cara, yaitu:
1. Dengan bantuan deret Taylor
2. Dengan hampiran polinom interpolasi
• Kedua cara tersebut menghasilkan rumus yang sama.
7

8. Penurunan Rumus dengan Deret Taylor
(a) Hampiran selisih-maju
Uraikan f(xi+1) di sekitar xi :
x
f(xi+1) = f(xi) + ( i+1
− x )i
f '(xi) +
2
( x − x )i+1 i
f "(xi) + ...
1! 2!
fi+1 = fi + hfi' + h2/2 fi " + .. .
hfi ' = fi+1 - fi - h2/2 fi " + ...
f − f
fi ' =
f
fi ' =
i+1
i+1
i
- h/2 fi "
h
− f i
+ O(h)
h
yang dalam hal ini, O(h) = h/2 f "(t), xi < t < xi+1
8

9. Untuk nilai-nilai f di x0 dan x1 persamaan rumusnya menjadi:
f − f
f0
1 0
' = + O(h)
h
yang dalam hal ini O(h) = h/2 f "(t), xi < t < xi+1 .
9

10. (b) Hampiran selisih-mundur
Uraikan f(xi-1) di sekitar xi :
x
f(xi-1) = f(xi) + ( i+1 − x ) xi
f '(xi) + (
2
− x )i+1 i
f "(xi) + ...
1! 2!
fi-1 = fi - hfi ' + h2/2 fi " + ...
hfi ' = fi - fi-1 + h2/2 fi " + ...
f − f
fi ' =
f
fi ' =
i
i
i −1
- h/2 fi " + ...
h
− f i −1
+ O(h),
h
yang dalam hal ini, O(h) = - h/2 f "(t), xi-1 < t < xi
10

11. Untuk nilai-nilai f di x0 dan x-1 persamaan rumusnya menjadi:
f0
f
' = 0 − f −1
+O(h)
h
yang dalam hal ini, O(h) = - h/2 f "(t), xi+1 < t < xi.
11

12. (a) Hampiran selisih-pusat
Kurangkan persamaan (P.7.4) dengan persamaan (P.7.6):
fi+1 - fi-1 = 2hfi' + h3/3 fi "' + ...
2hfi ' = fi+1 - fi-1
f − f
- h3/3 fi "' + ...
fi ' =
f
fi ' =
i+1
i+1
i −1
- h2/6 fi "' + ...
2h
− f i −1
+ O(h2),
2h
yang dalam hal ini, O(h2) = - h2/6 f "'(t), xi-1 < t < xi+1
Untuk nilai-nilai f di x-1 dan x1 persamaan rumusnya menjadi:
f1 − f −1 2
fo '= + O(h )
2h
yang dalam hal ini, O(h2) = - h/6 f "'(t), xi-1 < t < xi+1.
12

13. Rumus untuk Turunan Kedua, f ’’(x), dengan
Bantuan Deret Taylor
(a) Hampiran selisih-pusat
Tambahkan persamaan (P.7.4) dengan persamaan (P.7.6) di atas :
fi+1 + fi-1 = 2 fi + h2 fi " + h4/12 fi (4) + ...
fi+1 - 2fi + fi-1 = h2 fi " + h4/12 fi (4)
f − 2f + f
Jadi,
f i+1
fi" =
i+1
fi" =
− 2 f i + f i −1
2
h
i i −1
- h2/12 fi (4)
2
h
+ O(h2),
yang dalam hal ini, O(h2) = - h2/12 f (4)(t), xi-1 < t < xi+1
13

14. Untuk nilai-nilai f di x-1 , x0, dan x1 persamaan rumusnya menjadi:
1
f0" = f
− 2 f + f0 1
+ O(h2)2
h
yang dalam hal ini O(h2) = - h2/12 f (4)(t), xi-1 < t < xi+1.
14

15. (b) Hampiran selisih-mundur
Dengan cara yang sama seperti (a) di atas, diperoleh :
f
fi" =
i −2 − 2 f + fi −1 i
+ O(h),2
h
yang dalam hal ini O(h) = h f "(t), xi-2 < t < xi
Untuk nilai-nilai f di x-2 , x-1, dan x0 persamaan rumusnya :
f0
f
"= −2 − 2 f + f−1 0
+ O(h),2
h
yang dalam hal ini, O(h) = h f "(t) , xi-2 < t < xi
15

16. (c) Hampiran selisih-maju
Dengan cara yang sama seperti di atas, diperoleh :
i+2
fi" = f
− 2 f i+1 + f i
+ O(h),2
h
yang dalam hal ini, O(h) = - h f "(t), xi < t < xi+2
Untuk nilai-nilai f di x0 , x1, dan x2 persamaan rumusnya :
f0
f
"= 2
− 2 f + f1 0
+ O(h),2
h
yang dalam hal ini, O(h) = - h f "(t), x1 < t < xi+2.
16

17. Penurunan Rumus Turunan Numerik
dengan Polinom Interpolasi
• Polinom Newton-Gregory:
s Δf
f (x) ≈ pn(x) = f0 +
1 !
0
+ s(s-1)
Δ2 f0
2!
n
Δ f
Δ3 f0
+ s(s-1)(s-2) +
3!
0
s(s-1)(s-2)...(s- n+1)
n!
= F(s)
yang dalam hal ini, s = (x-x0)/h.
17

18. s Δf
f (x) ≈ pn(x) = f0 +
1 !
0
+ s(s-1)
Δ2 f0
2!
n
Δ f
Δ3 f0
+ s(s-1)(s-2) +
3!
0
s(s-1)(s-2)...(s- n+1)
n!
= F(s)
yang dalam hal ini, s = (x-x0)/h.
18

19. (a) Hampiran selisih-maju
- bila digunakan titik-titik x0 dan x1 :
f1 − f0
f '(x0) = 1/h ( Δf0) =
h
- bila digunakan titik-titik x0, x1, dan x2 :
f '(x0) = 1/h ( Δf0 + (s- 1/2) Δ2 f 0 )
untuk titik x0 → s = (x0 - x0)/h = 0, sehingga
f '(x0) = 1/h ( Δf0 - 1/2 Δ2f 0 )
= 1/h ( Δf0 - 1/2( Δf1 - Δf0) )
= 1/h (3/2 Δf0 - 1/2 Δf1)
= 1/h (3/2 f1 - 3/2 f0 - 1/2 f2+ 1/2 f1 )
= 1/h (-3/2 f0 + 2 f1 - 1/2 f2 )
−3f 0 +4f 1 − f 2
f '(x0 ) =
2h
19

20. (b) Hampiran selisih-mundur
- polinom interpolasi: Newton-Gregory mundur
- bila digunakan titik-titik x0 dan x-1 :
f − f0 −1
f '(x0) = 1/h ( ∇f0) =
h
20

21. (c) Hampiran selisih-pusat
- digunakan tiga titik x0 , x1 , dan x2 :
f '(x0) = 1/h ( Δf0 + (s - 1/2) Δ2f 0 )
untuk titik x1 → s = (x1 - x0)/h = h/h = 1, sehingga
f '(x1) = 1/h ( Δf0 + 1/2 Δ2f 0 )
= 1/h ( Δf0 + 1/2( Δf1 - Δf0) )
= 1/h (1/2 Δf0 + 1/2 Δf1)
= 1/2h ( f1 - f0 + f2 - f1 )
f2 − f0
=
2h
untuk titik x-1 , x0 , dan x1 :
f '(x0)
f 1 − f −1
=
2h
21

22. Rumus untuk Turunan Kedua, f "(x),
dengan Polinom Interpolasi
Turunan kedua f adalah
2
d f
2
dx
=
d df  ds
 
ds dx  dx
= 1/h (0 + Δ2f 0 + (s - 1) Δ3f 0 ) . 1/h
= 1/h2 ( Δ2 f0 + ( s - 1) Δ3f0 )
22

23. Misalkan untuk hampiran selisih-pusat, titik-titik yang digunakan x0 , x1 , dan x2 :
- pada titik x1 → s = (x1 - x0)/h = h/h = 1, sehingga
f "(x1) = 1/h2 ( Δ2f 0 + (1 - 1) Δ3f 0 )
= 1/h2 ( Δ2f 0 )
= 1/h2 ( Δf1 - Δf0)
2
= 1/h ( f2 - f1 + f1 + f0 )
= 1/h2 ( f0 - 2f1 + f2 )
- untuk titik x-1 , x0 , dan x1 :
f − 2 f + f
f " (x0
−1 0
) = 2
h
1
23

24. Ringkasan Rumus-Rumus Turunan
1. Rumus untuk turunan pertama
f0' =
f0' =
f0' =
f0' =
f 1 − f 0
+ O(h)
h
f − f0 −1
+ O(h)
h
f 1 − f −1
+ O(h2)
2h
−3 f 0 +4 f 1 − f 2
2h
− f 2 +8 f 1 −8 f −1
(selisih-maju)
(selisih-mundur)
(selisih-pusat)
+ O(h2) (selisih-maju)
+ f − 2
f0' = + O(h4)
12h
(selisih-pusat)
24

25. 2. Rumus untuk turunan kedua
f
f0" =
f
1 − 2f + f0 −1
+ O(h2)2
h
− 2f + f
(selisih-pusat)
−2
f0" =
h
f −2f
−1 0
+ O(h)2
+ f
(selisih-mundur)
2 1
f0" = 2
h
− f +4
0
+ O(h)
f −5 f +2 f
(selisih-maju)
3
f0" =
− f
2 1
12h
+16 f −30 f
0
+ O(h2)
+16 f − f
(selisih-maju)
2 1 0 −1 −2
f0" = + O(h4)2
12h
(selisih-pusat)
25

26. 3. Rumus untuk turunan ketiga
f
f0"' =
f
3 − 3f + 3f −2 1
3
h
− 2 f + 2 f −
f0
+ O(h) (selisih-maju)
f2 1 −1 −2
f0"' = 3
2h
4. Rumus untuk turunan keempat
f − 4 f + 6 f − 4 f
+ O(h2) (selisih-pusat)
+ f4
f0(iv) =
f − 4
3 2
4
h
f + 6 f − 4 f
1 0
+ O(h)
+ f
(selisih-maju)
2 1
f0(iv) = 0 −1 −2
+ O(h2)4
h
(selisih-pusat)
26

27. Contoh
Diberikan data dalam bentuk tabel sebagai berikut :
x f(x)
1.3 3.669
1.5 4.482
1.7 5.474
1.9 6.686
2.1 8.166
2.3 9.974
2.5 12.182
(a) Hitunglah f '(1.7) dengan rumus hampiran selisih-pusat orde O(h2) dan O(h4)
(b) Hitunglah f '(1.4)dengan rumus hampiran selisih-pusat orde O(h2)
(c) Rumus apa yang digunakan untuk menghitung f '(1.3) dan f '(2.5) ?
27

28. Penyelesaian:
(a) Orde O(h2):
f − f1 −1f0' =
2h
Ambil titik-titik x-1 = 1.5 dan x1 = 1.9, yang dalam hal ini x0 = 1.7 terletak di tengah
keduanya dengan h = 0.2.
f '(1.7) =
Orde O(h4):
− f
6.686 − 4.482
= 5.510
2 (0.2)
+8 f −8 f + f
(empat angka bena)
2 1
f0' =
12h
−1 2
28

29. Ambil titik-titik x-2 = 1.3 dan x-1 = 1.5 , x1 = 1.9, dan x2 = 2.1, yang dalam hal ini x0 =
1.7 terletak di pertengahannya.
f '(1.7)
(b) Orde O(h2):
−8.166 + 8 ( 6.686 ) −8 ( 4.482 ) + 3.669
=
12 (0.2)
= 5.473 (4 angka bena)
Ambil titik-titik x-1 = 1.3 dan x1 = 1.5, yang dalam hal ini x0 = 1.4 terletak di
tengahnya dan h = 0.1.
f '(1.4) =
4.482 − 3.669
= 4.065
2 (0.1)
(4 angka bena)
29

30. (c) Untuk menghitung f '(1.3) digunakan rumus hampiran selisih-maju, sebab x = 1.3
hanya mempunyai titik-titik sesudahnya (maju), tetapi tidak memiliki titik-titik sebelumnya.
Sebaliknya, untuk menghitung nilai f '(2.5) digunakan rumus hampiran selisih-mundur,
sebab x = 2.5 hanya mempunyai titik-titik sebelumnya (mundur).
Hampiran selisih-maju :
f f
f0' =
f '(1.3) =
1 − 0
+ O(h)
h
4.482 − 3.669
= 4.065
Hampiran selisih-mundur :
f
f0' = 0 − f −1
+ O(h)
h
f '(2.5) = 12.182 −9.974 = 11.04
30

31. Terapan Turunan Numerik dalam Bidang
Pengolahan Citra
• Citra digital dapat disajikan oleh matriks f yang berukuran M
N dengan bentuk


f
f
11 f f 12 1N

f f
f =  21
 M

fM 1
22 2n
M M M
f fM 2 MN




• Tiap elemen matriks adalah bilangan bulat dalam rentang
[0..255] untuk citra 8 bit.
31

32. • Salah satu proses yang terdapat dalam pengolahan
citra ialah pendeteksian tepi.
• Tepi merupakan feature yang penting pada suatu citra.
• Tepi didefinisikan sebagai perubahan intensitas yang
besar dalam jarak yang singkat.
• Perbedaan intensitas inilah yang menampakkan rincian
pada gambar. Tepi memberikan informasi batas-batas
objek dengan lingkungannya atau dengan objek yang
lain, feature untuk mengidentifikasi objek, dan untuk
terapan penapisan citra.
32

33. 33

34. 34

35. • Salah satu pendekatamyang dipakai dalam
pendeteksian sisi adalah dengan kemiringan
diferensial (differential gradient).
• Secara matematis perubahan intensitas yang
besar dalam jarak yang sangat singkat dapat
dipandang sebagai suatu fungsi yang memiliki
kemiringan yang besar.
• Pengukuran kemiringan suatu fungsi dilakukan
dengan menghitung turunan pertamanya.
35

36. • Dalam citra digital, pendeteksian tepi dapat dilakukan dengan
cara yang mirip, yaitu dengan turunan pertamanya secara
parsial dalam ruang diskrit:
∇ f(x, y) =
∂f / ∂x 
 
f 
= x 
∂f / ∂y  fy 
• yang dalam hal ini kedua turunan parsial didefinisikan sebagai
D1(x) =
D1( y) =
∂f ( x, y )
∂x
∂f ( x, y )
∂y
f ( x+Δx, y ) − f ( x, y )
≈
Δx
f ( x, y+Δy ) − f ( x, y )
≈
Δy
36

37. Biasanya Δx = Δy = 1, sehingga persamaan turunan pertama menjadi:
D1
D1
∂f (x,
(x) =
∂x
∂f (x,
(y) =
∂y
y)
= f (x +1,y) − f (x, y)
y)
= f (x, y+1) − f (x, y)
37

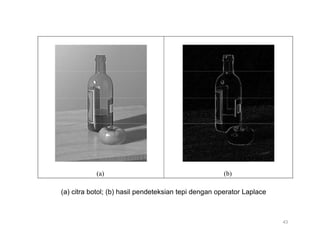
38. • Kekuatan tepi pada setiap pixel citra dihitung dengan
rumus:
G[f(x,y)] = | fx2 | + | fy2 |
• atau dengan rumus
G[f(x,y)] = max ( fx2 | , | fy2 |)
• Suatu pixel dianggap sebagai pixel sisi jika kekuatan
tepinya di atas nilai ambang (threshold) tertentu.
38

39. • D1(x) dan D1( y) merupakan hampiran selisih-maju.
Hampiran lain yang dipakai adalah hampiran selisih-
pusat, yaitu:
D2(x) =
D2(y) =
∂f ( x, y )
≈
∂x
∂f ( x, y )
≈
∂y
f ( x+Δx, y ) − f(x − Δx , y
2 Δ x
f ( x, y+Δy ) − f(x, y − Δy )
2 Δ y
)
39

40. • Operator lain yang digunakan untuk mendeteksi sisi
adalah yang berdasarkan pada operasi turunan
kedua, yang dikenal dengan operator Laplace
(Laplacian).
• Operator Laplace mendeteksi lokasi tepi lebih akurat
khususnya pada tepi yang curam.
40

41. f(x)
∂f / ∂x
∂2f / ∂x2
•
(a) Tepi landai (b) Tepi curam
41

42. • Jika digunakan hampiran selisih-maju, maka operator Laplace
diturunkan sebagai berikut:
∇2f =
2 2
∂ f ∂ f
+2 2
∂x ∂y
= D1(D1(x)) + D1( D1( y))
1 1
= D1 ( f(x + Δx, y) - D1( f(x,y)) +
Δx
D1( f(x, y))
1 f ( x x+Δx, y ) − f ( x + Δx ,y
D1( f(x, y + Δy) -
Δy
) f ( x+ Δx, y ) − f ( x, y ) 
=
Δx
1

 Δx
f ( x, y +Δy+Δy
−
) − f ( x, y + Δy ) f
+
Δx 
( x, y+ Δy ) − f ( x, y ) 
=
Δy
f ( x

 Δy
+ 2 Δ x, y ) − 2 f ( x+Δx,
( Δx )2
− 
Δy 
y ) + f ( x, y )
+
f (x, y + 2 Δy)− 2 f (x, y+Δy )+ f (x, y)
(Δy)2
42

43. (a) (b)
(a) citra botol; (b) hasil pendeteksian tepi dengan operator Laplace
43

44. CONTOH PROGRAM
#include // pembacaan cout dan cin.
#include // tampilan standar input output.
#include // di gunakan untuk membuat teks antarmuka pengguna.
#include // prototype fungsi untuk pustaka matematika.
main() // program utama
{ // pembuka program .
int i=1, k; // pendeklarasian variabel dengan menggunakan tipe data integer.
float x0, x1, xr, fx0, fx1, E, e=0.00001; // pendeklarasian variabel dengan
menggunakan tipe data float.
clrscr(); // untuk menghapus data yang tidak perlu.
gotoxy(18,6);cout<<" METODE SECANT f(x)=2x^2-
5x+1"<gotoxy(18,7);cout<<"---------------------------------------"; // tampilan output
tabel.
gotoxy(14,9);cout<< "Masukkan Nilai Awal : ";cin>>x0; // input nilai awal
gotoxy(14,10);cout<<"Masukkan Nilai Akhir : ";cin>>x1; // input nilai akhir
gotoxy(7,12);cout<<"+------------------------------------------------+"<

45. LANJUTAN PROGRAM
gotoxy(8,13);cout<<"iterasi"; // pembacaan nilai iterasi.
gotoxy(18,13);cout<<"x0"; // pembacaan nilai x0 (masukan nilai awal).
gotoxy(24,13);cout<<"x1"; // pembacaan nilai x1 (masukan nilai akhir).
gotoxy(30,13);cout<<"xr"; // pembacaan nilai xr.
gotoxy(34,13);cout<<"f(x0)"; // pembacaan nilai f(x0) turunan nilai dari x0.
gotoxy(43,13);cout<<"f(x1)"; // pembacaan nilai f(x1) turunan nilai dari x1.
gotoxy(50,13);cout<<"E"; // pembacaan nilai error.
gotoxy(7,14);cout<<"+------------------------------------------------+"<k=15; //
do // menggunakan perulangan.
{ // pembuka program
fx0 = (2*(x0*x0))-(5*x0)+1; // rumus untuk pemanggilan nilai f(x0).
fx1 = (2*(x1*x1))-(5*x1)+1; // rumus untuk pemanggilan nilai f(x1).
xr = x1-(fx1*((x1-x0)/(fx1-fx0))); // rumus untuk pemanggilan nilai xr.
E = fabs((xr-x1)/xr); // rumus untuk pemanggilan nilai E.

46. LANJUTAN PROGRAM
gotoxy(10,k);cout<gotoxy(16,k);printf("%.3f",x0); // pemanggilan tampilan output hasil
hitungan x0.
gotoxy(22,k);printf("%.3f",x1); // pemanggilan tampilan output hasil hitungan x1.
gotoxy(28,k);printf("%.3f",xr); // pemanggilan tampilan output hasil hitungan xr.
gotoxy(34,k);printf("%.3f",fx0); // pemanggilan tampilan output hasil hitungan f(x0).
gotoxy(42,k);printf("%.3f",fx1); // pemanggilan tampilan output hasil hitungan f(x1).
gotoxy(50,k);printf("%.3f",E); // // pemanggilan tampilan output hasil hitungan E.
x0=x1; // pembacaan nilai x0 = x1.
x1=xr; // pembacaan nilai x1 = xr.
k++; //
i++; // pembacaan urutan nomor iterasi.
} // penutup program.
while(E>e); //
gotoxy(7,k);cout<<"+------------------------------------------------+"<getch();
return 0;
}

47. OUT PUT