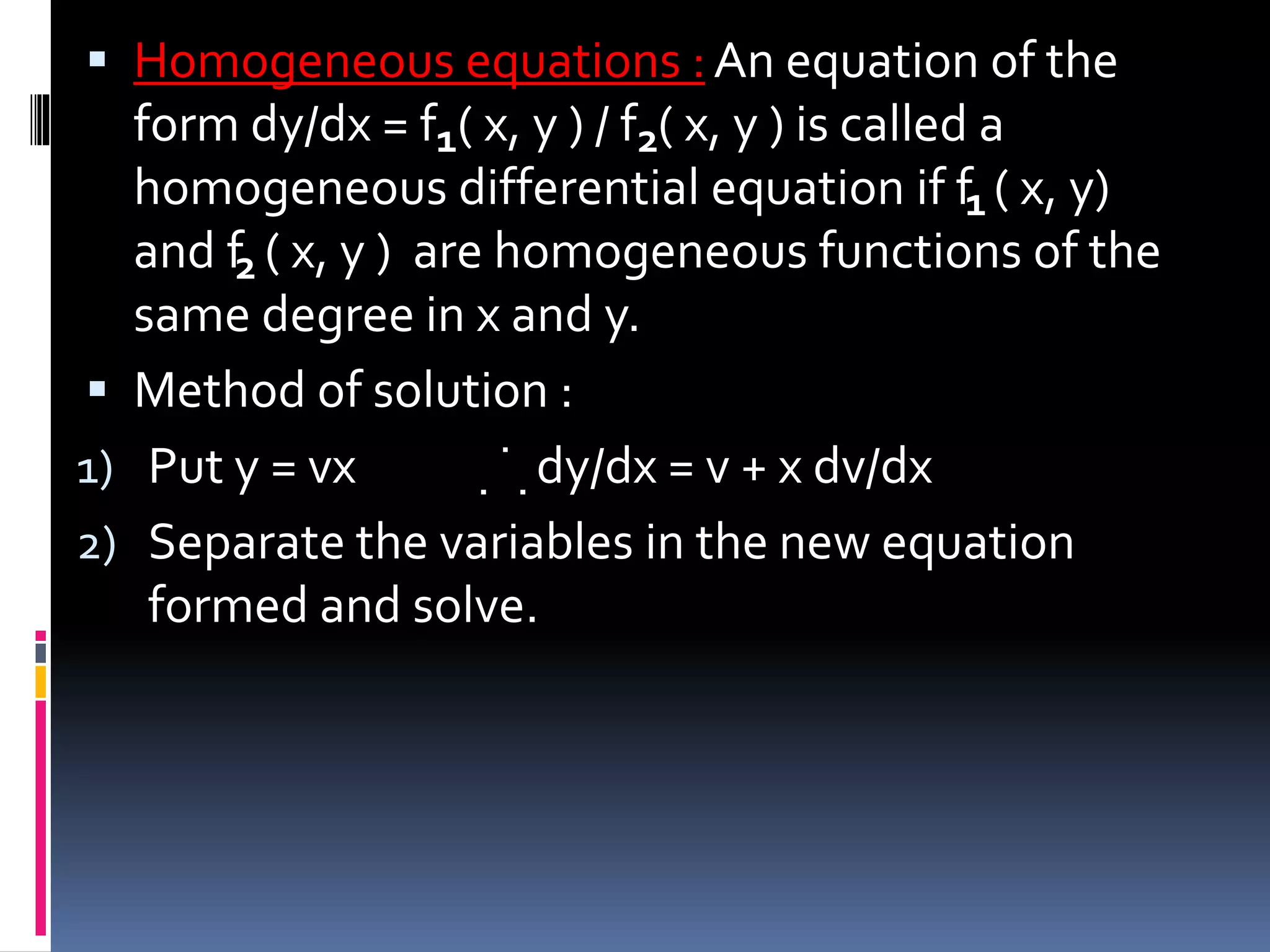This document discusses first order differential equations. It defines differential equations and classifies them as ordinary or partial based on whether they involve derivatives with respect to a single or multiple variables. First order differential equations are classified into four types: variable separable, homogeneous, linear, and exact. The document provides examples of each type and explains their general forms and solution methods like separating variables, making substitutions, and integrating.

1. Differential equations of first order

2. Introduction
 Definition of differential equation
 Classification of differential equations
 The order and the degree of a differential
equation
 Classification of first order differential
equation

3. Definition of differential
equation
 An equation involving differentials or differential
coefficients is called a differential equation.
Thus,
1) dy = sin x dx
2) d y/dx = 0
3) y = x dy/dx + a/dy/dx
4) ∂z/∂x + ∂z/∂y = 1
5) ∂ z/∂x + ∂ z/∂y = 0
2 2
2 2 2 2

4. Classification of differential
equations
1) Ordinary differential equations.
2) Partial differential equations.
 Ordinary differential equations :
ordinary differential equations are those
which involves ordinary derivatives with respect
to a single independent variable.
Thus equations,
1) dy = sin x dx
2) d y/dx = 0
3) y = x dy/dx + a/dy/dx
2 2

5.  Partial differential equations :
partial differential equations are
those which involves partial derivatives with
respects to two or more independent variables.
Thus equations,
1) ∂z/∂x + ∂z/∂y = 1
2) ∂ z/∂x + ∂ z/∂y = 0
2 2 2 2

6. The order and the degree of a
differential equation
 The order of the differential equation is the
order of the highest derivative appearing in the
differential equation.
 The degree of a differential equation is the
degree of the highest derivative, when the
derivatives are free from radicals and fractions.
 Example : ( d y/dx ) + (dy/dx) = c
order : 2
degree : 2
2 22 3

7. Formation of a differential
equation
 Ordinary differential equations are formed by
elimination of arbitrary constants.
 Example : from the differential equation of
simple harmonic motion given by,
x = a sin (ωt + )
 Solution : there are two arbitrary constants a
and therefore, we differentiate it twice w.r.t. t,
we have, dx/dt = ωa cos (ωt + ) and
d x/dt = -ω a sin (ωt + ) = -ω x thus,
d x/dt + ω x = 0 which is the required d.e.
2 2 2 2
2 2 2

8. Classification of first order
differential equation
1) Variable separable.
2) Homogeneous equations.
3) Linear equations.
4) Exact equations.

9.  Variable separable method : the general form of
this type of equation is M(x) dx + N(y) dy = 0
 Which can be solved by direct integration as
ʃ M(x) dx + ʃ N(y) dy = c
 Example (1) : x dx + siny dy = 0
ʃ x dx + ʃ siny dy = 0
x /3 + ( -cosy ) = c
(2) : 9y y + 4x = 0
9y dy/dx + 4x = 0
ʃ 9y dy + ʃ 4x dx = 0
9 y /2 + 4 x /2 = c
2
2
3
І
2 2

10.  Homogeneous equations :An equation of the
form dy/dx = f ( x, y ) / f ( x, y ) is called a
homogeneous differential equation if f ( x, y)
and f ( x, y ) are homogeneous functions of the
same degree in x and y.
 Method of solution :
1) Put y = vx dy/dx = v + x dv/dx
2) Separate the variables in the new equation
formed and solve.
1
1
2
2
.
. .

11.  Example : solve (x - y ) dy = 2xy dx
 Solution : dy/dx = 2xy/x - y
put y = vx dy/dx = v + x dy/dx
therefore v + x dv/dx = 2v/1-v
or x dv/dx = 2v/1-v - v
= v + v / 1 – v
or 1 – v / v(1 + v ) dv = dx/x
or (1/v – 2v/1 + v ) dv = dx/x
integrating, we get
log v – log (1 + v ) = log x + log c
or log ( v /1 + v ) = log cx
2 2
2 2
2
2
.
. .
3 2
22
2
2
2

12. or v/1 + v = cx or (y/x) 1/1 + (y/x) = cx
or y/x x /x + y = cx
or y = c ( x + y )
or x + y - 1/c y = 0
or x + y - by = 0 which is required solution.
2 2
. 2 2 2
2 2
2 2
2 2