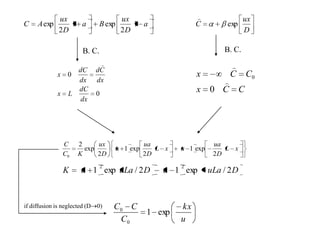
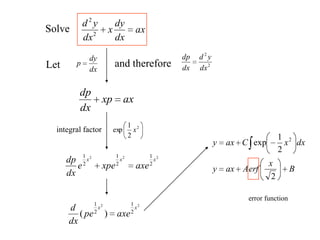
1) Ordinary differential equations relate a dependent variable to one or more independent variables by means of differential coefficients. They can be classified based on order, degree, whether they are linear or non-linear, and type (exact, separable variables, homogeneous). 2) First order differential equations can sometimes be solved by separation of variables, or by finding an integrating factor. Homogeneous equations can be transformed by substitution. 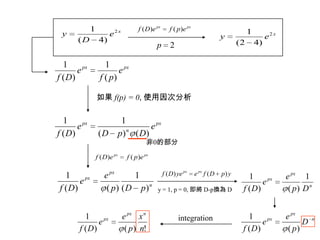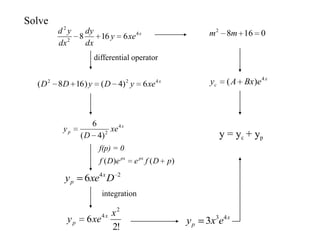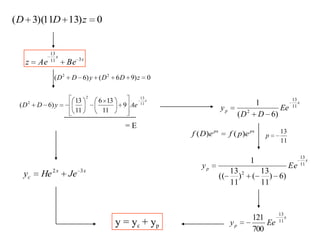3) Second order linear differential equations can be reduced to a system of two first order equations. The complementary function and particular solutions combine to form the general solution. Unequal or equal roots of the characteristic equation determine the form of the complementary function.

1. Ordinary
Differential
Equations

2. Differential equation
• An equation relating a dependent variable to one
or more independent variables by means of its
differential coefficients with respect to the
independent variables is called a “differential
equation”.
xey
dx
dy
dx
yd x
cos44)( 2
3
3
Ordinary differential equation --------
only one independent variable involved: x
)( 2
2
2
2
2
2
z
T
y
T
x
T
k
T
Cp
Partial differential equation ---------------
more than one independent variable involved: x, y, z,

3. Order and degree
• The order of a differential equation is equal to the
order of the highest differential coefficient that it
contains.
• The degree of a differential equation is the highest
power of the highest order differential coefficient
that the equation contains after it has been
rationalized.
xey
dx
dy
dx
yd x
cos44)( 2
3
3
3rd order O.D.E.
1st degree O.D.E.

4. Linear or non-linear
• Differential equations are said to be non-
linear if any products exist between the
dependent variable and its derivatives, or
between the derivatives themselves.
xey
dx
dy
dx
yd x
cos44)( 2
3
3
Product between two derivatives ---- non-linear
xy
dx
dy
cos4 2
Product between the dependent variable themselves ---- non-linear

5. First order differential equations
• No general method of solutions of 1st
O.D.E.s because of their different degrees
of complexity.
• Possible to classify them as:
– exact equations
– equations in which the variables can be
separated
– homogenous equations
– equations solvable by an integrating factor

6. Exact equations
• Exact? 0),(),( dyyxNdxyxM
dFdy
y
F
dx
x
F
General solution: F (x,y) = C
For example
0)2(cossin3
dx
dy
yxxyx

7. Separable-variables equations
• In the most simple first order differential
equations, the independent variable and its
differential can be separated from the
dependent variable and its differential by
the equality sign, using nothing more than
the normal processes of elementary algebra.
For example
x
dx
dy
y sin

8. Homogeneous equations
• Homogeneous/nearly homogeneous?
• A differential equation of the type,
• Such an equation can be solved by making the
substitution u = y/x and thereafter integrating the
transformed equation.
x
y
f
dx
dy
is termed a homogeneous differential equation
of the first order.

9. Homogeneous equation example
• Liquid benzene is to be chlorinated batchwise by sparging chlorine gas
into a reaction kettle containing the benzene. If the reactor contains
such an efficient agitator that all the chlorine which enters the reactor
undergoes chemical reaction, and only the hydrogen chloride gas
liberated escapes from the vessel, estimate how much chlorine must be
added to give the maximum yield of monochlorbenzene. The reaction
is assumed to take place isothermally at 55 C when the ratios of the
specific reaction rate constants are:
k1 = 8 k2 ; k2 = 30 k3
C6H6+Cl2 C6H5Cl +HCl
C6H5Cl+Cl2 C6H4Cl2 + HCl
C6H4Cl2 + Cl2 C6H3Cl3 + HCl

10. Take a basis of 1 mole of benzene fed to the reactor and introduce
the following variables to represent the stage of system at time ,
p = moles of chlorine present
q = moles of benzene present
r = moles of monochlorbenzene present
s = moles of dichlorbenzene present
t = moles of trichlorbenzene present
Then q + r + s + t = 1
and the total amount of chlorine consumed is: y = r + 2s + 3t
From the material balances : in - out = accumulation
d
dt
Vpsk
d
ds
Vpskprk
d
dr
Vprkpqk
d
dq
Vpqk
3
32
21
10
1)(
1
2
q
r
k
k
dq
dr
u = r/q

11. Equations solved by integrating factor
• There exists a factor by which the equation can be multiplied
so that the one side becomes a complete differential
equation. The factor is called “the integrating factor”.
QPy
dx
dy
where P and Q are functions of x only
Assuming the integrating factor R is a function of x only, then
)(Ry
dx
d
dx
dR
y
dx
dy
R
RQyRP
dx
dy
R
PdxR exp is the integrating factor

12. Example
Solve
2
3
exp
2
4 x
y
dx
dy
xy
Let z = 1/y3
4
3
ydy
dz
dx
dy
ydx
dz
4
3 2
3
exp33
2
x
dx
dz
xz
integral factor
2
3
exp3exp
2
x
xdx
3
2
3
exp
2
3
exp3
22
x
dx
dzx
xz
3
2
3
exp
2
x
z
dx
d
Cx
x
z 3
2
3
exp
2
Cx
x
y
3
2
3
exp
1 2
3

13. Summary of 1st O.D.E.
• First order linear differential equations
occasionally arise in chemical engineering
problems in the field of heat transfer,
momentum transfer and mass transfer.

14. First O.D.E. in heat transfer
An elevated horizontal cylindrical tank 1 m diameter and 2 m long is insulated with
asbestos lagging of thickness l = 4 cm, and is employed as a maturing vessel for a
batch chemical process. Liquid at 95 C is charged into the tank and allowed to
mature over 5 days. If the data below applies, calculated the final temperature of the
liquid and give a plot of the liquid temperature as a function of time.
Liquid film coefficient of heat transfer (h1) = 150 W/m2C
Thermal conductivity of asbestos (k) = 0.2 W/m C
Surface coefficient of heat transfer by convection and radiation (h2) = 10 W/m2C
Density of liquid ( ) = 103 kg/m3
Heat capacity of liquid (s) = 2500 J/kgC
Atmospheric temperature at time of charging = 20 C
Atmospheric temperature (t) t = 10 + 10 cos ( /12)
Time in hours ( )
Heat loss through supports is negligible. The thermal capacity of the lagging can be ignored.

15. T
Area of tank (A) = ( x 1 x 2) + 2 ( 1 / 4 x 12 ) = 2.5 m2
Tw
Ts
Rate of heat loss by liquid = h1 A (T - Tw)
Rate of heat loss through lagging = kA/l (Tw - Ts)
Rate of heat loss from the exposed surface of the lagging = h2 A (Ts - t)
t
At steady state, the three rates are equal:
)()()( 21 tTAhTT
l
kA
TTAh ssww tTTs 674.0326.0
Considering the thermal equilibrium of the liquid,
input rate - output rate = accumulation rate
d
dT
sVtTAh s )(0 2
)12/cos(235.0235.00235.0 T
d
dT
B.C. = 0 , T = 95

16. Second O.D.E.
• Purpose: reduce to 1st O.D.E.
• Likely to be reduced equations:
– Non-linear
• Equations where the dependent variable does not occur explicitly.
• Equations where the independent variable does not occur explicitly.
• Homogeneous equations.
– Linear
• The coefficients in the equation are constant
• The coefficients are functions of the independent variable.

17. Non-linear 2nd O.D.E.
- Equations where the dependent variables does not
occur explicitly
• They are solved by differentiation followed by the
p substitution.
• When the p substitution is made in this case, the
second derivative of y is replaced by the first
derivative of p thus eliminating y completely and
producing a first O.D.E. in p and x.

18. Solve ax
dx
dy
x
dx
yd
2
2
Let dx
dy
p 2
2
dx
yd
dx
dp
and therefore
axxp
dx
dp
2
2
1
exp xintegral factor
222
2
1
2
1
2
1
xxx
axexpee
dx
dp
22
2
1
2
1
)(
xx
axepe
dx
d
B
x
Aerfaxy
dxxCaxy
2
2
1
exp 2
error function

19. Non-linear 2nd O.D.E.
- Equations where the independent variables does
not occur explicitly
• They are solved by differentiation followed by the
p substitution.
• When the p substitution is made in this case, the
second derivative of y is replaced as
Let
dx
dy
p
dy
dp
p
dx
dy
dy
dp
dx
dp
dx
yd
2
2

20. Solve 2
2
2
)(1
dx
dy
dx
yd
y
Let dx
dy
p and therefore
2
1 p
dy
dp
yp
Separating the variables
dy
dp
p
dx
yd
2
2
dy
y
dp
p
p 1
12
)1ln(
2
1
lnln 2
pay
)1( 22
ya
dx
dy
p
bay
a
x
ya
dy
x
)(sinh1
)1(
1
22

21. Non-linear 2nd O.D.E.- Homogeneous equations
• The homogeneous 1st O.D.E. was in the form:
• The corresponding dimensionless group containing
the 2nd differential coefficient is
• In general, the dimensionless group containing the
nth coefficient is
• The second order homogenous differential equation
can be expressed in a form analogous to , viz.
x
y
f
dx
dy
2
2
dx
yd
x
n
n
n
dx
yd
x 1
x
y
f
dx
dy
dx
dy
x
y
f
dx
yd
x ,2
2 Assuming u = y/x
dx
du
xuf
dx
ud
x ,2
2
2
Assuming x = et
dt
du
uf
dt
du
dt
ud
,2
2
If in this form, called homogeneous 2nd ODE

22. Solve
2
22
2
2
2
2
dx
dy
xy
dx
yd
yx
Dividing by 2xy
2
2
2
2
1
2
1
dx
dy
y
x
x
y
dx
yd
x
homogeneous
2
2
2
2
dt
du
dt
ud
u
dx
dy
x
y
f
dx
yd
x ,2
2
Let uxy
2
2
2
2
2
22
dx
du
x
dx
du
ux
dx
ud
ux
Let t
ex
dt
du
p
2
2 p
du
dp
up
2
)ln( CxBxy
Axy Singular solution
General solution

23. A graphite electrode 15 cm in diameter passes through a furnace wall into a water
cooler which takes the form of a water sleeve. The length of the electrode between
the outside of the furnace wall and its entry into the cooling jacket is 30 cm; and as
a safety precaution the electrode in insulated thermally and electrically in this section,
so that the outside furnace temperature of the insulation does not exceed 50 C.
If the lagging is of uniform thickness and the mean overall coefficient of heat transfer
from the electrode to the surrounding atmosphere is taken to be 1.7 W/C m2 of
surface of electrode; and the temperature of the electrode just outside the furnace is
1500 C, estimate the duty of the water cooler if the temperature of the electrode at
the entrance to the cooler is to be 150 C.
The following additional information is given.
Surrounding temperature = 20 C
Thermal conductivity of graphite kT = k0 - T = 152.6 - 0.056 T W/m C
The temperature of the electrode may be assumed uniform at any cross-section.
x
T
T0

24. x
T
T0
The sectional area of the electrode A = 1/4 x 0.152 = 0.0177 m2
A heat balance over the length of electrode x at distance x from the furnace is
input - output = accumulation
0)()( 0 xTTDUx
dx
dT
Ak
dx
d
dx
dT
Ak
dx
dT
Ak TTT
where U = overall heat transfer coefficient from the electrode to the surroundings
D = electrode diameter
xTT
A
DU
x
dx
dT
k
dx
d
T )( 0
0)()( 00 TT
dx
dT
Tk
dx
d
0)()( 0
2
2
2
0 TT
dx
dT
dx
Td
Tk
dx
dT
p 2
2
dx
Td
dT
dp
p
0)()( 0
2
0 TTp
dT
dp
pTk

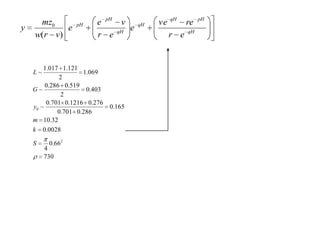
25. 0)()( 0
2
0 TTp
dT
dp
pTk
zp2
)( 0TTy
022])[( 0 yz
dy
dz
yTk
Integrating factor 2
00
00
2
exp yTk
yTk
dy
])(32))(([
)(
3
0
2
00
0
TTTTTkC
dTTk
x

26. Linear differential equations
• They are frequently encountered in most chemical
engineering fields of study, ranging from heat,
mass, and momentum transfer to applied chemical
reaction kinetics.
• The general linear differential equation of the nth
order having constant coefficients may be written:
)(... 11
1
10 xyP
dx
dy
P
dx
yd
P
dx
yd
P nnn
n
n
n
where (x) is any function of x.

27. 2nd order linear differential equations
The general equation can be expressed in the form
)(2
2
xRy
dx
dy
Q
dx
yd
P
where P,Q, and R are constant coefficients
Let the dependent variable y be replaced by the sum of the two new variables: y = u + v
Therefore
)(2
2
2
2
xRv
dx
dv
Q
dx
vd
PRu
dx
du
Q
dx
ud
P
If v is a particular solution of the original differential equation
02
2
Ru
dx
du
Q
dx
ud
P
The general solution of the linear differential equation will be the sum of
a “complementary function” and a “particular solution”.
purpose

28. The complementary function
02
2
Ry
dx
dy
Q
dx
yd
P
Let the solution assumed to be:
mx
meAy mx
mmeA
dx
dy mx
m emA
dx
yd 2
2
2
0)( 2
RQmPmeA mx
m
auxiliary equation (characteristic equation)
Unequal roots
Equal roots
Real roots
Complex roots

29. Unequal roots to auxiliary equation
• Let the roots of the auxiliary equation be distinct and of
values m1 and m2. Therefore, the solutions of the auxiliary
equation are:
• The most general solution will be
• If m1 and m2 are complex it is customary to replace the
complex exponential functions with their equivalent
trigonometric forms.
xm
eAy 1
1
xm
eAy 2
2
xmxm
eAeAy 21
21

30. Solve 0652
2
y
dx
dy
dx
yd
auxiliary function
0652
mm
3
2
2
1
m
m
xx
BeAey 32

31. Equal roots to auxiliary equation
• Let the roots of the auxiliary equation equal and of value
m1 = m2 = m. Therefore, the solution of the auxiliary
equation is: mx
Aey
mxmx
mVe
dx
dV
e
dx
dymx
VeyLet
mxmxmx
Vem
dx
dV
me
dx
Vd
e
dx
yd 2
2
2
2
2
2
where V is a function of x 02
2
Ry
dx
dy
Q
dx
yd
P
02
2
dx
Vd
DCxV
mx
edCxy )(

32. Solve 0962
2
y
dx
dy
dx
yd
auxiliary function
0962
mm
321 mm
x
eBxAy 3
)(

33. Solve 0542
2
y
dx
dy
dx
yd
auxiliary function
0542
mm
im 2
xixi
BeAey )2()2(
)sincos(2
xFxEey x

34. Particular integrals
• Two methods will be introduced to obtain
the particular solution of a second linear
O.D.E.
– The method of undetermined coefficients
• confined to linear equations with constant
coefficients and particular form of (x)
– The method of inverse operators
• general applicability
)(2
2
xRy
dx
dy
Q
dx
yd
P

35. Method of undetermined coefficients
• When (x) is constant, say C, a particular integral of
equation is
• When (x) is a polynomial of the form
where all the coefficients are constants. The form of a
particular integral is
• When (x) is of the form Terx, where T and r are
constants. The form of a particular integral is
)(2
2
xRy
dx
dy
Q
dx
yd
P
RCy /
n
n xaxaxaa ...2
210
n
n xxxy ...2
210
rx
ey

36. Method of undetermined coefficients
• When (x) is of the form G sin nx + H cos nx, where
G and H are constants, the form of a particular
solution is
• Modified procedure when a term in the particular
integral duplicates a term in the complementary
function.
)(2
2
xRy
dx
dy
Q
dx
yd
P
nxMnxLy cossin

37. Solve 3
2
2
8444 xxy
dx
dy
dx
yd
32
sxrxqxpy
2
32 sxrxq
dx
dy
sxr
dx
yd
622
2
3322
84)(4)32(4)62( xxsxrxqxpsxrxqsxr
Equating coefficients of equal powers of x
84
0124
4486
0442
s
sr
qrs
pqr
32
26107 xxxyp
0442
mmmauxiliary equation
x
c eBxAy 2
)(
pcgeneral yyy

38. Method of inverse operators
• Sometimes, it is convenient to refer to the
symbol “D” as the differential operator:
n
n
n
dx
yd
yD
dx
yd
yDDyD
dx
dy
Dy
...
)( 2
2
2
But,
2
2
)(
dx
dy
Dy
y
dx
dy
dx
yd
232
2
yDDyDDyDyyD )2)(1()23(23 22

39. The differential operator D can be treated as an ordinary algebraic
quantity with certain limitations.
(1) The distribution law:
A(B+C) = AB + AC
which applies to the differential operator D
(2) The commutative law:
AB = BA
which does not in general apply to the differential operator D
Dxy xDy
(D+1)(D+2)y = (D+2)(D+1)y
(3) The associative law:
(AB)C = A(BC)
which does not in general apply to the differential operator D
D(Dy) = (DD)y
D(xy) = (Dx)y + x(Dy)
The basic laws of algebra thus apply to the pure operators, but the
relative order of operators and variables must be maintained.

40. Differential operator to exponentials
pxpx
pxnpxn
pxpx
epfeDf
epeD
peDe
)()(
...
pxpx
eppeDD )23()23( 22
ypDfeyeDf
ypDeyeD
ypDeyeD
ypDeyDeDyeyeD
pxpx
npxpxn
pxpx
pxpxpxpx
)())((
)()(
...
)()(
)()(
22
More convenient!

41. Differential operator to
trigonometrical functions
ipxnipxnipxnn
eipeDeDpxD )Im(ImIm)(sin
pxpppxD
pxppxD
pxpppxD
pxppxD
pxipxe
nn
nn
nn
nn
ipx
sin)()(cos
cos)()(cos
cos)()(sin
sin)()(sin
sincos
212
22
212
22
where “Im” represents the imaginary part of the function which follows it.

42. The inverse operator
The operator D signifies differentiation, i.e.
)()( xfdxxfD )()( 1
xfDdxxf
•D-1 is the “inverse operator” and is an “intergrating” operator.
•It can be treated as an algebraic quantity in exactly the same manner as D

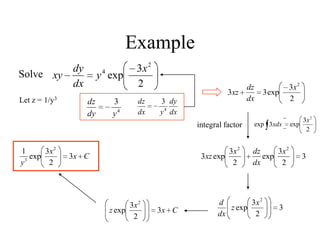
43. Solve x
ey
dx
dy 2
4
differential operator
x
eyD 2
)4(
x
e
D
y 2
)4(
1
1...])
4
1
()
4
1
()
4
1
(1[
4
1 322
DDDey x
binomial expansion
=2
x
ey 2
2
1
pxpx
epfeDf )()(
x
e
D
y 2
)
4
1
1(4
1
2p
x
ey 2
)42(
1
...])
2
1
()
2
1
()
2
1
(1[
4
1 322x
ey

44. x
e
D
y 2
)4(
1 pxpx
epfeDf )()(
2p
x
ey 2
)42(
1
pxpx
e
pf
e
Df )(
1
)(
1
如果 f(p) = 0, 使用因次分析
px
n
px
e
DpD
e
Df )()(
1
)(
1
n
px
px
pDp
e
e
Df )(
1
)()(
1
pxpx
epfeDf )()(
n
px
px
Dp
e
e
Df
1
)()(
1
非0的部分
ypDfeyeDf pxpx
)()(
y = 1, p = 0, 即將 D-p換為 D
n
px
px
D
p
e
e
Df )()(
1integration
!)()(
1
n
x
p
e
e
Df
npx
px

45. Solve
x
xey
dx
dy
dx
yd 4
2
2
6168
differential operator
x
xeyDyDD 422
6)4()168(
01682
mm
x
c eBxAy 4
)(
x
p xe
D
y 4
2
)4(
6
24
6 Dxey x
p
f(p) = 0
)()( pDfeeDf pxpx
integration
!2
6
2
4 x
xey x
p
x
p exy 43
3
y = yc + yp

46. Solve
23
2
2
346 xxy
dx
dy
dx
yd
differential operator
232
34)2)(3()6( xxyDDyDD
062
mm
xx
c BeAey 23
)34(
)2)(3(
1 23
xx
DD
yp
expanding each term by binomial theorem
y = yc + yp
)34(
)2(
1
)3(
1
5
1 23
xx
DD
yp
)34(...
16842
1
...
812793
1
5
1 23
3232
xx
DDDDDD
yp
...0
1296
2413
216
)624(7
36
612
6
34 223
xxxxx
yp

47. O.D.E in Chemical Engineering
• A tubular reactor of length L and 1 m2 in cross section is
employed to carry out a first order chemical reaction in
which a material A is converted to a product B,
• The specific reaction rate constant is k s-1. If the feed rate is
u m3/s, the feed concentration of A is Co, and the
diffusivity of A is assumed to be constant at D m2/s.
Determine the concentration of A as a function of length
along the reactor. It is assumed that there is no volume
change during the reaction, and that steady state conditions
are established.
A B

48. u
C0
x
L
x
u
C
A material balance can be taken over the element of length x at a distance x fom the inlet
The concentraion will vary in the entry section
due to diffusion, but will not vary in the section
following the reactor. (Wehner and Wilhelm, 1956)
x x+ x
Bulk flow of A
Diffusion of A
uC
x
dx
dC
D
dx
d
dx
dC
D
dx
dC
D
x
dx
dC
uuC
Input - Output + Generation = Accumulation
0xkCx
dx
dC
D
dx
d
dx
dC
Dx
dx
dC
uuC
dx
dC
DuC
分開兩個section
Ce

49. 0xkCx
dx
dC
D
dx
d
dx
dC
Dx
dx
dC
uuC
dx
dC
DuC
dividing by x
0kC
dx
dC
D
dx
d
dx
dC
u
rearranging
02
2
kC
dx
dC
u
dx
Cd
D
auxillary function
02
kumDm
a
D
ux
Ba
D
ux
AC 1
2
exp1
2
exp
In the entry section
02
2
dx
Cd
u
dx
Cd
D

auxillary function
02
umDm
D
ux
C exp

2
/41 ukDa

50. a
D
ux
Ba
D
ux
AC 1
2
exp1
2
exp
D
ux
C exp

B. C.
0
0
dx
dC
Lx
dx
Cd
dx
dC
x

B. C.
CCx
CCx


0
0
xL
D
ua
axL
D
ua
a
D
ux
KC
C
2
exp1
2
exp1
2
exp
2
0
DuLaaDuLaaK 2/exp12/exp1
22
if diffusion is neglected (D 0)
u
kx
C
CC
exp1
0
0

51. The continuous hydrolysis of
tallow in a spray column 連續牛油水解
1.017 kg/s of a tallow fat mixed with 0.286 kg/s of high pressure hot water is fed into
the base of a spray column operated at a temperature 232 C and a pressure of
4.14 MN/m2. 0.519kg/s of water at the same temperature and pressure is sprayed
into the top of the column and descends in the form of droplets through the rising fat
phase. Glycerine is generated in the fat phase by the hydrolysis reaction and is extracted
by the descending water so that 0.701 kg/s of final extract containing 12.16% glycerine
is withdrawn continuously from the column base. Simultaneously 1.121 kg/s of fatty
acid raffinate containing 0.24% glycerine leaves the top of the column.
If the effective height of the column is 2.2 m and the diameter 0.66 m, the glycerine
equivalent in the entering tallow 8.53% and the distribution ratio of glycerine between
the water and the fat phase at the column temperature and pressure is 10.32, estimate
the concentration of glycerine in each phase as a function of column height. Also find
out what fraction of the tower height is required principally for the chemical reaction.
The hydrolysis reaction is pseudo first order and the specific reaction rate constant is
0.0028 s-1.
Glycerin, 甘油

52. Tallow fat Hot water
G kg/s
Extract
Raffinate
L kg/s
L kg/s
xH
zH
x0
z0
y0
G kg/s
yH
h
x
z
x+ x
z+ z y+ y
y
h
x = weight fraction of glycerine in raffinate
y = weight fraction of glycerine in extract
y*= weight fraction of glycerine in extract in equilibrium with x
z = weight fraction of hydrolysable fat in raffinate

53. Consider the changes occurring in the element of column of height h:
Glycerine transferred from fat to water phase, hyyKaS )*(
S: sectional area of tower
a: interfacial area per volume of tower
K: overall mass transter coefficient
Rate of destruction of fat by hydrolysis, hSzk
A glycerine balance over the element h is:
hyyKaS
w
hSzk
h
dh
dx
xLLx *
Rate of production of glycerine by hydrolysis, whSzk /
k: specific reaction rate constant
: mass of fat per unit volume of column (730 kg/m3)
w: kg fat per kg glycetine
A glycerine balance between the element and the base of the tower is:
00
w
Lz
w
Lz
Lx
L kg/s
xH
zH
x0
z0
y0
G kg/s
yH
h
x
z
x+ x
z+ z y+ y
y
h
The glycerine equilibrium between the phases is:
mxy*
hyyKaSGyh
dh
dy
yG *
in the fat phase
in the extract phase
00GyGy
in the fat phase
in the extract phase

54. 02
2
0
0
2
dh
dy
L
KaSm
dh
yd
dh
dy
G
KaS
dh
dy
y
G
KaS
L
Sk
yy
L
mG
w
mz
LG
KaSk
L
mG
r
L
Sk
p
)1(r
G
KaS
q
w
mz
ry
r
pq
pqy
dh
dy
qp
dh
yd 0
02
2
1
)( 2nd O.D.E. with constant coefficients
Complementary function
Particular solution
0)(2
pqmqpm Constant at the right hand side, yp = C/R
)exp()exp( qhBphAyc pq
w
mz
ry
r
pq
yp /
1
0
0

55. w
mz
ry
r
qhBphAy 0
0
1
1
)exp()exp(
B.C.
0,
0,0
yHh
xh
We don’t really want x here!
Apply the equations two slides earlier (replace y* with mx)
0,
,0 0
yHh
yyh
dh
dy
q
r
ymx
1
We don’t know y0, either
)exp()exp(
1
qhqBphpA
q
r
ymx
0,0 yyh
pHqHqhpHpHqHpHqH
reveeveeer
w
mz
ry
r
revey )()(
1
1
)( 0
0
q
prpq
v
Substitute y0 in terms of other variables

56. qH
pHqH
qH
qH
pH
pH
er
reve
e
er
ve
e
vrw
mz
y
)(
0
730
66.0
4
0028.0
32.10
165.0
286.0701.0
276.01216.0701.0
~
403.0
2
519.0286.0
~
069.1
2
121.1017.1
~
2
0
S
k
m
y
G
L

57. Simultaneous differential
equations
• These are groups of differential equations
containing more than one dependent
variable but only one independent variable.
• In these equations, all the derivatives of the
different dependent variables are with
respect to the one independent variable.
Our purpose: Use algebraic elemination of the variables until only
one differential equation relating two of the variables remains.

58. Elimination of variable
Independent variable or dependent variables?
),(
),(
2
1
yxf
dt
dy
yxf
dt
dx
Elimination of independent variable
),(
),(
2
1
yxf
yxf
dy
dx
較少用
Elimination of one or more dependent variables
It involves with equations of high order and
it would be better to make use of matrices
Solving differential equations simultaneously using
matrices will be introduced later in the term

59. Elimination of dependent variables
Solve
0)23()103(
0)96()6(
22
22
zDDyDD
and
zDDyDD
0)1)(2()5)(2(
0)3()2)(3( 2
zDDyDD
and
zDyDD
)5(D
)3(D
0)1)(2)(3()5)(2)(3(
0)3)(5()5)(2)(3( 2
zDDDyDDD
and
zDDyDDD
0)23()158()3(
0)1)(2)(3()3)(5(
22
2
zDDDDD
zDDDzDD
0)1311)(3( zDD

60. 0)1311)(3( zDD
x
x
BeAez 311
13
0)96()6( 22
zDDyDD
x
AeyDD 11
132
2
9
11
136
11
13
)6(
= E
x
p Ee
DD
y 11
13
2
)6(
1
xx
c JeHey 32
pxpx
epfeDf )()(
11
13
p
x
p Eey 11
13
2
)6)
11
13
()
11
13
((
1
x
p Eey 11
13
700
121
y = yc + yp