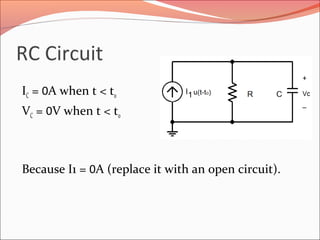
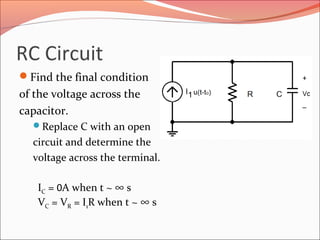
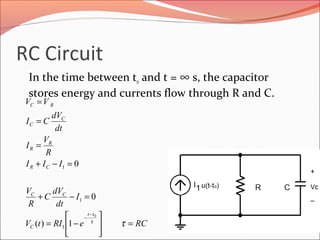
The document discusses the transient response of RC and RL circuits, explaining how capacitors and inductors store energy when subjected to step function sources or switched voltage/current sources. It details the determination of final conditions for capacitor voltage and inductor current, emphasizing the importance of time constants and superposition in circuit analysis. General equations for forced responses in both types of circuits are also provided, noting that steady-state is reached after approximately 5 time constants.

1. INITIAL AND FINAL CONDITION
FOR CIRCUIT

2. Contents
Explain the transient response of a RC circuit
As the capacitor stores energy when there is:
 a transition in a unit step function source, u(t-to)
 or a voltage or current source is switched into the circuit.
Explain the transient response of a RL circuit
As the inductor stores energy when there is:
 a transition in a unit step function source, u(t-to)
 or a voltage or current source is switched into the circuit.
Also known as a forced response to an independent source

3. RC Circuit
IC = 0A when t < to
VC = 0V when t < to
Because I1 = 0A (replace it with an open circuit).

4. RC Circuit
Find the final condition
of the voltage across the
capacitor.
Replace C with an open
circuit and determine the
voltage across the terminal.
IC = 0A when t ~ ∞ s
VC = VR = I1R when t ~ ∞ s

5. RC Circuit
In the time between to and t = ∞ s, the capacitor
stores energy and currents flow through R and C.
RCeRItV
I
dt
dV
C
R
V
III
R
V
I
dt
dV
CI
VV
tt
C
CC
CR
R
R
C
C
RC
=





−=
=−+
=−+
=
=
=
−
−
ττ
1)(
0
0
0
1
1
1

6. RL Circuit

7. RL Circuit (con’t)
Initial condition is not important as the magnitude of
the voltage source in the circuit is equal to 0V when t
≤ to.
Since the voltage source has only been turned on at t =
to, the circuit at t ≤ to is as shown below.
 As the inductor has not stored any energy because no power
source has been connected to the circuit as of yet, all voltages
and currents are equal to zero.

8. RL Circuit
So, the final condition of the inductor current needs
to be calculated after the voltage source has switched
on.
Replace L with a short circuit and calculate IL(∞).

9. Final Condition
R
V
I
II
VV
R
RL
L
1
)(
0)(
=
=∞
=∞

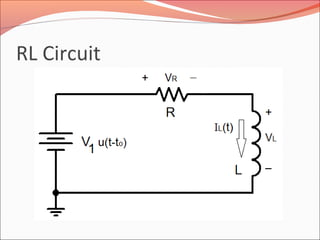
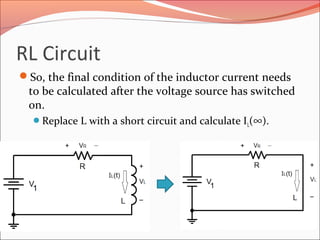
10. RL Circuit
[ ]τ/)(1
1
1
1)(
0
0
ott
L
L
L
R
L
e
R
V
tI
L
V
I
L
R
dt
dI
VRI
dt
dI
−−
−=
=−+
=−+
R
L
=τ
dt
dI
LV
RVII
VVV
L
L
RRL
RL
=
==
=++−
/
01

11. Electronic Response
Typically, we say that the currents and voltages in a
circuit have reached steady-state once 5τ have passed
after a change has been made to the value of a current
or voltage source in the circuit.
In a circuit with a forced response, percentage-wise
how close is the value of the voltage across a capacitor
in an RC circuit to its final value at 5τ?

12. Complete Response
Is equal to the natural response of the circuit plus the
forced response
Use superposition to determine the final equations for
voltage across components and the currents flowing
through them.

13. Example -1
Suppose there were two unit step function sources in
the circuit.

14. Example -1 (con’t)
The solution for Vc would be the result of
superposition where:
I2 = 0A, I1 is left on
 The solution is a forced response since I1 turns on at t = t1
I1 = 0A, I2 is left on
 The solution is a natural response since I2 turns off at t = t2

15. Example -1 (con’t)
1
)t-(t
-
1
1
whene-1)(
when0)(
1
ttRItV
ttVtV
RC
C
C
>





=
<=

16. Example -1 (con’t)
2
)t-(t
-
2
22
whene)(
when)(
2
ttRItV
ttRItV
RC
C
C
>−=
<−=

17. Example -1 (con’t)
If t1 < t2
2
)t-(t
-
2
)t-(t
-
1
212
)t-(t
-
1
12
whenee-1)(
whene1)(
henw0)(
21
1
ttRIRItV
tttRIRItV
ttRIVtV
RCRC
C
RC
C
C
>−





=
<<−





−=
<−=

18. General Equations
[ ]
[ ]
[ ]
[ ]
RL
eII
L
tV
eIIItI
RC
eVV
C
tI
eVVVtV
t
LLL
t
LLLL
t
CCC
t
CCCC
/
)0()()(
)()0()()(
)0()()(
)()0()()(
/
/
/
/
=
−∞=
∞−+∞=
=
−∞=
∞−+∞=
−
−
−
−
τ
τ
τ
τ
τ
τ
τ
τ
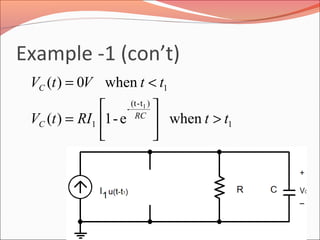
When a
voltage or
current source
changes its
magnitude at
t= 0s in a
simple RC or
RL circuit.
Equations for a simple RC circuit
Equations for a simple RL circuit

19. Summary
The final condition for:
the capacitor voltage (Vo) is determined by replacing the
capacitor with an open circuit and then calculating the
voltage across the terminals.
The inductor current (Io) is determined by replacing the
inductor with a short circuit and then calculating the current
flowing through the short.
The time constant for:
an RC circuit is τ = RC and an RL circuit is τ = L/R
The general equations for the forced response of:
the voltage across a capacitor is
the current through an inductor is
[ ]
[ ] o
tt
oL
o
tt
oC
tteItI
tteVtV
o
o
>−=
>−=
−−
−−
when1)(
when1)(
/)(
/)(
τ
τ

20. Summary
General equations when the magnitude of a voltage
or current source in the circuit changes at t = 0s for
the:
voltage across a capacitor is
current through an inductor is
Superposition should be used if there are multiple
voltage and/or current sources that change the
magnitude of their output as a function of time.
[ ]
[ ] τ
τ
/
/
)()0()()(
)()0()()(
t
LLLL
t
CCCC
eIIItI
eVVVtV
−
−
∞−+∞=
∞−+∞=

21. References
E draw max (for drawing)
Electrical circuit