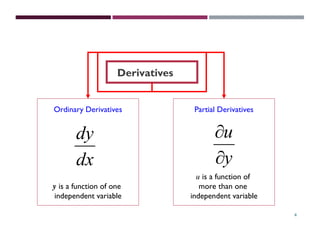
The document is a presentation on ordinary differential equations (ODE) led by Nouman Iftikhar, covering definitions, classifications, and methods of solving both linear and nonlinear ODEs. It discusses key concepts such as order, linearity, and the difference between boundary-value and initial-value problems, and introduces various solution techniques including analytical and numerical methods. The content is based on the references provided, primarily focusing on first and second order differential equations and their solutions.

1. 1
Here is Nouman Iftikhar
And I am going to perform the presenation of Ordinary
Differential Equation (ODE) Taught By Honorable
Dr. Saima Mushtaq

2. Topic : Ordinary Differential Equations
Philip H. Dybvig
2
Reference: Lecture Notes by Paul Dawkins, 2007, page 20-33,
page 102-121,page 137-155 and page 340-344

3. INTRODUCTION TO ORDINARY
DIFFERENTIAL EQUATIONS (ODE)
 Recall basic definitions of ODE
 Order
 linearity
 initial conditions
 solution
 Classify ODE based on( order, linearity, conditions)
 Classify the solution methods
3

4. DERIVATIVES
Derivatives
dx
dy
4
Partial Derivatives
u is a function of
more than one
independent variable
Ordinary Derivatives
y is a function of one
independent variable
y
u



5. DIFFERENTIAL EQUATIONS
Differential
Equations
1
6
2
2

 xy
dx
y
d
5
involve one or more
partial derivatives of
unknown functions
Ordinary Differential Equations
involve one or more
Ordinary derivatives of
unknown functions
0
2
2
2
2






x
u
y
u
Partial Differential Equations

6. ORDINARY DIFFERENTIAL EQUATIONS
ORDINARY DIFFERENTIAL EQUATIONS
6
)
cos(
2
5
:
2
2
x
y
dx
dy
dx
y
d
e
y
dx
dy
Examples
x





Ordinary Differential Equations (ODE) involve one or
more ordinary derivatives of unknown functions with
respect to one independent variable
y(x): unknown function
x: independent variable

7. ORDER OF A DIFFERENTIAL EQUATION
ORDER OF A DIFFERENTIAL EQUATION
7
1
2
)
cos(
2
5
:
4
3
2
2
2
2
















y
dx
dy
dx
y
d
x
y
dx
dy
dx
y
d
e
y
dx
dy
Examples
x
The order of an ordinary differential equations is the order
of the highest order derivative
Second order ODE
First order ODE
Second order ODE

8. SOLUTION OF A DIFFERENTIAL EQUATION
SOLUTION OF A DIFFERENTIAL EQUATION
0
)
(
)
(
)
(
:
Proof
)
(












t
t
t
t
e
e
t
x
dt
t
dx
e
dt
t
dx
e
t
x
Solution
8
A solution to a differential equation is a function that
satisfies the equation.
0
)
(
)
(
:

 t
x
dt
t
dx
Example

9. LINEAR ODE
LINEAR ODE
9
1
)
cos(
2
5
:
3
2
2
2
2
2
















y
dx
dy
dx
y
d
x
y
x
dx
dy
dx
y
d
e
y
dx
dy
Examples
x
An ODE is linear if the unknown function and its derivatives
appear to power one. No product of the unknown function
and/or its derivatives
Linear ODE
Linear ODE
Non-linear ODE
)
(
)
(
)
(
)
(
'
)
(
)
(
)
(
)
(
)
( 0
1
1
1 x
g
x
y
x
a
x
y
x
a
x
y
x
a
x
y
x
a n
n
n
n 



 
 

10. BOUNDARY-VALUE AND INITIALVALUE PROBLEMS
Boundary-Value Problems
 The auxiliary conditions are not at
one point of the independent
variable
 More difficult to solve than initial
value problem
5
.
1
)
2
(
,
1
)
0
(
'
2
'
' 2




 
y
y
e
y
y
y x
10
Initial-Value Problems
 The auxiliary conditions
are at one point of the
independent variable
5
.
2
)
0
(
'
,
1
)
0
(
'
2
'
' 2




 
y
y
e
y
y
y x
same different

11. CLASSIFICATION OF ODE
ODE can be classified in different ways
 Order
 First order ODE
 Second order ODE
 Nth
order ODE
 Linearity
 Linear ODE
 Nonlinear ODE
 Auxiliary conditions
 Initial value problems
 Boundary value problems 11

12. SOLUTIONS
 Analytical Solutions to ODE are available for linear ODE and special classes of
nonlinear differential equations.
 Numerical method are used to obtain a graph or a table of the unknown
function
 We focus on solving first order linear ODE and second order linear ODE and
Euler equation
12

13. FIRST ORDER LINEAR DIFFERENTIAL
EQUATIONS
 Def:A first order differential equation is
said to be linear if it can be written
13
)
(
)
( x
g
y
x
p
y 



14. FIRST ORDER LINEAR DIFFERENTIAL
EQUATIONS
 How to solve first-order linear ODE ?
Sol:
14
)
1
(
)
(
)
( x
g
y
x
p
y 


)
2
(
)
(
)
(
)
(
)
(
)
( x
g
x
y
x
p
x
dx
dy
x 

 

Multiplying both sides by , called an integrating factor,
gives
)
(x

assuming we get
)
3
(
),
(
'
)
(
)
( x
x
p
x 
 
)
4
(
)
(
)
(
)
(
'
)
( x
g
x
y
x
dx
dy
x 

 


15. FIRST ORDER LINEAR DIFFERENTIAL
EQUATIONS
15
By product rule, (4) becomes
Now, we need to solve from (3)
)
(
)
(
)
(
'
)
(
'
)
(
)
( x
p
x
x
x
x
p
x 






)
6
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
5
(
)
(
)
(
))'
(
)
(
(
1
1
x
c
dx
x
g
x
x
y
c
dx
x
g
x
x
y
x
x
g
x
x
y
x















)
(x


16. FIRST ORDER LINEAR DIFFERENTIAL
EQUATIONS
16
)
7
(
)
(
)
(
)
(
ln
)
(
))'
(
(ln
)
(
)
(
)
(
'
)
(
3
)
(
2
2 












dx
x
p
c
dx
x
p
e
c
e
x
c
dx
x
p
x
x
p
x
x
p
x
x





to get rid of one constant, we can use
)
9
(
)
(
)
(
)
(
then
is
equation
al
differenti
order
first
linear
a
o
solution t
The
)
8
(
)
(
)
(
)
(






dx
x
p
dx
x
p
e
c
dx
x
g
x
x
y
e
x



17. SUMMARY OF THE SOLUTION
PROCESS
 Put the differential equation in the form (1)
 Find the integrating factor, using (8)
 Multiply both sides of (1) by and write the left
side of (1) as
 Integrate both sides
 Solve for the solution
17
)
(x

)
(x

))'
(
)
(
( x
y
x

)
(x
y

18. EXAMPLE 1
Sol:
18
x
e
y
y 2



 
 
x
x
x
x
x
x
x
x
dx
dx
dx
x
p
dx
x
p
e
ce
c
e
e
c
dx
e
e
e
c
dx
e
e
e
c
dx
x
g
e
e
x
y
2
2
2
)
1
(
)
1
(
)
(
)
(
)
(
)
(











 








 












19. EXAMPLE 2
Sol:
19
2
1
)
1
(
,
2
' 2



 y
x
x
y
xy
 
.
12
7
3
1
4
1
2
1
c,
get
to
condition
initial
Apply the
3
1
4
1
3
1
4
1
)
1
(
)
1
(
)
(
)
(
1
2
'
2
2
3
4
2
2
2
2
2
)
(
)
(





































 
















c
c
cx
x
x
c
x
x
x
c
dx
x
x
x
c
dx
x
e
e
c
dx
x
g
e
e
x
y
x
y
x
y
dx
x
dx
x
dx
x
p
dx
x
p

20. SECOND ORDER LINEAR DIFFERENTIAL EQUATIONS
 Homogeneous Second Order Linear Differential Equations
o real roots, complex roots and repeated roots
 Non-homogeneous Second Order Linear Differential
Equations
o Undetermined Coefficients Method
 Euler Equations
20

21. )
(
'
'
' x
g
cy
by
ay 


where a, b and c are constant coefficients
Let the dependent variable y be replaced by the sum of the two
new variables: y = u + v
Therefore
    )
(
'
'
'
'
'
' x
g
cv
bv
av
cu
bu
au 





If v is a particular solution of the original differential equation
The general solution of the linear differential equation will
be the sum of a “complementary function” and a “particular
solution”.
purpose
Second Order Linear Differential Equations
The general equation can be expressed in the form
  0
'
'
' 

 cu
bu
au
21

22. 0
'
'
' 

 cy
by
ay
Let the solution assumed to be:
rx
e
y 
rx
re
dx
dy
 rx
e
r
dx
y
d 2
2
2

0
)
( 2


 c
br
ar
erx
characteristic equation Real, distinct roots
Double roots
Complex roots
The Complementary Function (solution of the
homogeneous equation)
22

23. 23
x
r
e
y 1
 x
r
e
y 2

x
r
x
r
e
c
e
c
y 2
1
2
1 

Real, Distinct Roots to Characteristic Equation
• Let the roots of the characteristic equation be real, distinct
and of values r1 and r2. Therefore, the solutions of the
characteristic equation are:
• The general solution will be
0
6
'
5
'
' 

 y
y
y 0
6
5
2


 r
r
3
2
2
1


r
r x
x
e
c
e
c
y 3
2
2
1 

• Example

24. rx
e
y 
rx
rx
rVe
V
e
y 

 '
'
rx
Ve
y 
Let
rx
rx
rx
Ve
r
V
re
V
e
y 2
'
2
'
'
'
'
and 


where V is a
function of x
0
'
'
' 

 cy
by
ay
0
)
(
'
' 
x
V d
cx
V 

rx
rx
rx
rx
xe
c
e
c
e
d
cx
be
y 2
1
)
( 




Equal Roots to Characteristic Equation
• Let the roots of the characteristic equation equal and of value r1 =
r2 = r. Therefore, the solution of the characteristic equation is:
0
c
br
ar2


 0
b
ar
2 

24

25. )).
sin(
)
(cos(
,
))
sin(
)
(cos(
)
(
2
)
(
1
x
i
x
e
e
y
x
i
x
e
e
y
x
x
i
x
x
i


















).
sin(
cos
:
is
d.e.
the
o
solution t
geneal
the
Therefore,
equation.
al
differenti
the
to
solutions
two
are
and
that
see
easy to
is
It
)
sin(
)
(
2
1
)
(
),
cos(
)
(
2
1
)
(
2
1
2
1
2
1
x
e
c
x)
(
e
c
y(x)
v
u
x
e
y
y
i
x
v
x
e
y
y
x
u
λx
λx
x
x



 









Complex Roots to Characteristic
Equation
Let the roots of the characteristic equation be complex in
the form r1,2 =λ±µi. Therefore, the solution of the
characteristic equation is:
25

26. (I) Solve 0
9
'
6
'
' 

 y
y
y
characteristic equation
0
9
6
2


 r
r
3
2
1 

r
r
x
e
x
c
c
y 3
2
1 )
( 


Examples
(II) Solve 0
5
'
4
'
' 

 y
y
y
characteristic equation
0
5
4
2


 r
r
i
r 
2
2
,
1
)
sin
cos
( 2
1
2
x
c
x
c
e
y x


26

27. When g(x) is a polynomial of the form
where all the coefficients are constants. The form of a particular solution is
)
(
'
'
' x
g
cy
by
ay 


c
k
y /

n
n x
a
x
a
x
a
a 


 ...
2
2
1
0
n
n x
x
x
y 


 



 ...
2
2
1
0
Non-homogeneous Differential Equations
(Method of Undetermined Coefficients)
When g(x) is constant, say k, a particular solution of equation is
27

28. Example
Solve 3
8
4
4
'
4
'
' x
x
y
y
y 



3
2
sx
rx
qx
p
y 



2
3
2
' sx
rx
q
y 


sx
r
y 6
2
'
' 

3
3
2
2
8
4
)
(
4
)
3
2
(
4
)
6
2
( x
x
sx
rx
qx
p
sx
rx
q
sx
r 









equating coefficients of equal powers of x
8
4
0
12
4
4
4
8
6
0
4
4
2









s
s
r
q
r
s
p
q
r
3
2
2
6
10
7 x
x
x
yp 



0
4
4
2


 r
r
characteristic equation
x
c e
x
c
c
y 2
2
1 )
( 

3
2
2
2
1 2
6
10
7
)
( x
x
x
e
x
c
c
y
y
y
x
p
c








0
4
'
4
'
' 

 y
y
y
complementary function
2

r
28

29. Non-homogeneous Differential Equations
(Method of Undetermined Coefficients)
rx
Ae
y 
• When g(x) is of the form Terx
, where T and r are constants. The
form of a particular solution is
c
br
ar
T
A


 2
• When g(x) is of the form Csinnx + Dcosnx, where C and D are
constants, the form of a particular solution is
nx
F
nx
E
y cos
sin 

2
2
2
2
2
)
(
)
(
b
n
a
n
c
nbD
C
a
n
c
E





2
2
2
2
2
)
(
)
(
b
n
a
n
c
nbD
C
a
n
c
F





29

30. Example
Solve 18
'
6
'
'
3 
 y
y
Cx
y 
C
y 
'
0
'
' 
y
18
)
C
(
6
)
0
(
3 

3
C 

x
yp 3


0
6
3 2

 r
r
characteristic equation
x
c e
c
c
y 2
2
1 

x
p
c
e
c
c
x
y
y
y
2
2
1
3 





0
'
6
'
'
3 
 y
y
complementary function
2
,
0 2
1 
 r
r
30

31. Example
Solve
x
e
y
y
y 4
7
8
'
10
'
'
3 



x
Cxe
y 4


x
Ce
x
y 4
)
4
1
(
' 


x
Ce
x
y 4
)
8
16
(
'
' 


7
10
24 

 C
C
2
1


C
x
p xe
y 4
2
1 


0
)
4
)(
2
3
(
8
10
3 2





 r
r
r
r
characteristic equation
x
x
c Be
Ae
y 4
3
/
2 


x
x
x
p
c
Be
Ae
xe
y
y
y
4
3
/
2
4
2
1 







0
8
'
10
'
'
3 

 y
y
y
complementary function
4
,
3
/
2 2
1 

 r
r
31

32. Example
Solve x
y
y
y 2
cos
52
6
'
'
' 


x
D
x
C
y 2
sin
2
cos 

)
2
cos
2
sin
(
2
' x
D
x
C
y 


)
2
sin
2
cos
(
4
'
' x
D
x
C
y 


0
10
2
52
2
10






D
C
D
C
1
5



D
C
x
x
yp 2
sin
2
cos
5 


0
)
3
)(
2
(
6
2





 r
r
r
r
characteristic equation
x
x
c Be
Ae
y 3
2 


x
x
Be
Ae
y
y
y
x
x
p
c
2
sin
2
cos
5
3
2







0
6
'
'
' 

 y
y
y
complementary function
3
,
2 2
1 

 r
r
32

33. EULER EQUATIONS
 Def: Euler equations
 Assuming x>0 and all solutions are of the form
y(x) = xr
 Plug into the differential equation to get the
characteristic equation
33
0
'
'
'
2


 cy
bxy
y
ax
.
0
)
(
)
1
( 


 c
r
b
r
ar

34. SOLVING EULER EQUATIONS: (CASE I)
34
• The characteristic equation has two different real
solutions r1 and r2.
• In this case the functions y = xr1 and y = xr2 are
both solutions to the original equation. The general
solution is: 2
1
2
1
)
( r
r
x
c
x
c
x
y 

.
x
c
x
c
y(x)
.
r
,
r
r-
)
r(r-
y
xy
y
x
3
2
2
5
1
2
1
2
3
2
5
0
15
3
1
2
:
is
equation
stic
characteri
the
,
0
15
'
3
'
'
2













Example:

35. SOLVING EULER EQUATIONS: (CASE II)
35
• The characteristic equation has two equal roots r1
= r2=r.
• In this case the functions y = xr
and y = xr
lnx are
both solutions to the original equation. The general
solution is: )
ln
(
)
( 2
1 x
c
c
x
x
y r


x.
x
c
x
c
y(x)
.
r
r
)
r(r-
y
xy
y
x
ln
4
0
16
7
1
:
is
equation
stic
characteri
the
,
0
16
'
7
'
'
4
2
4
1
2











Example:

36. SOLVING EULER EQUATIONS: (CASE III)
36
• The characteristic equation has two complex
roots r1,2 = λ±µi.
x))
(μ
c
x)
(μ
(c
x
y(x)
x
ix
x
x
e
x
λ
x
i
i
ln
sin
ln
cos
:
be
ill
solution w
general
the
roots,
complex
of
case
in the
So,
)
ln
sin(
)
ln
cos(
2
1
ln
)
(




 


 





.
x
x
c
x
x
c
y(x)
i.
r
r
)
r(r-
y
xy
y
x
)
ln
3
sin(
)
ln
3
cos(
3
1
0
4
3
1
:
is
equation
stic
characteri
the
,
0
4
'
3
'
'
1
2
1
1
2
,
1
2















Example: