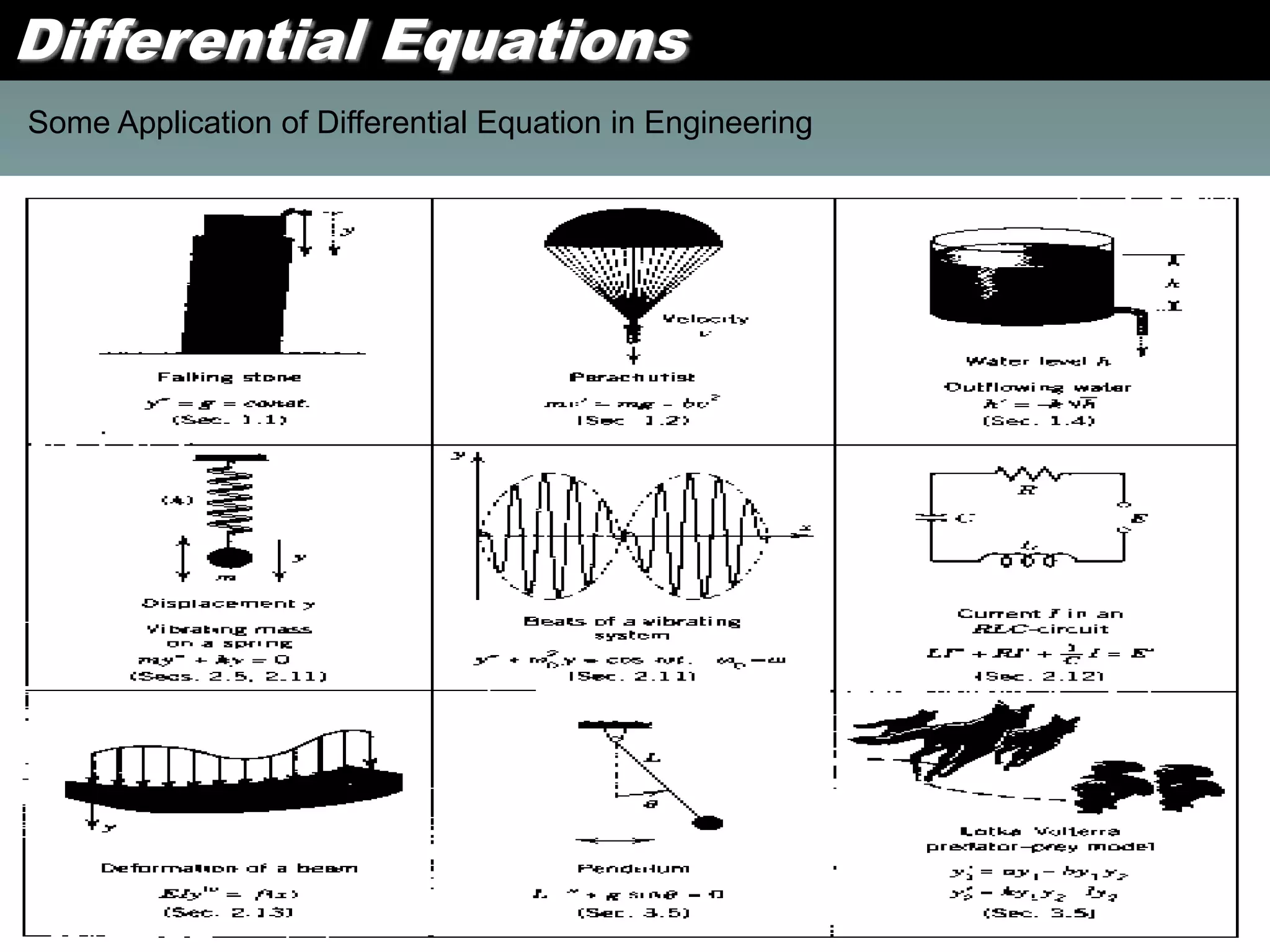
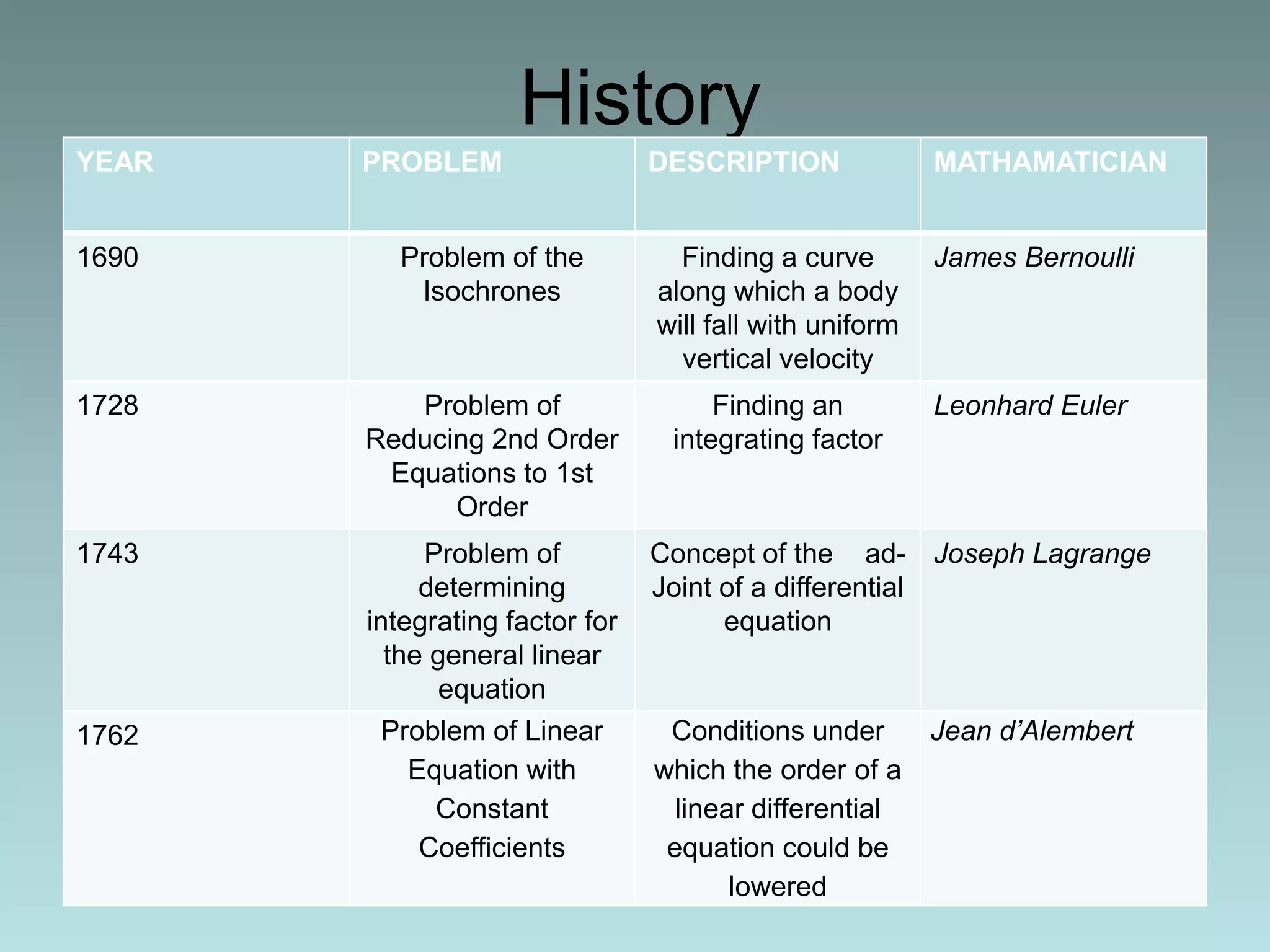
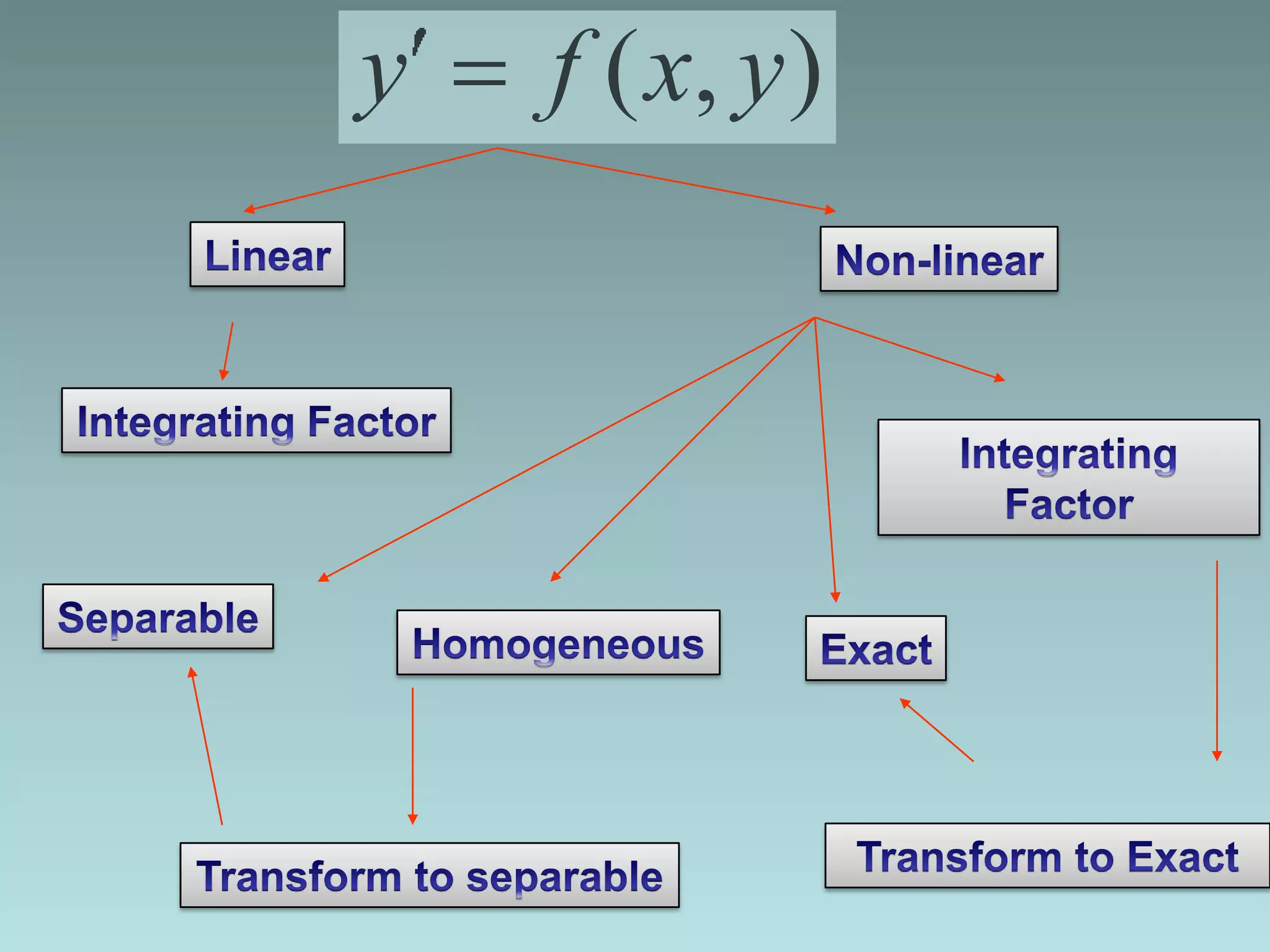
1. A differential equation relates an unknown function and its derivatives, and can be ordinary (involving one variable) or partial (involving partial derivatives). 2. Linear differential equations have dependent variables and derivatives that are of degree one, and coefficients that do not depend on the dependent variable. 3. Common methods for solving first-order linear differential equations include separation of variables, homogeneous equations, and exact equations.

1. Linear Differential Equation
By
Nofal Umair

2. Introduction to Differential
Equations

3. Differential Equations
 An equation which involves unknown function of one or several variables that
relates the values of the function itself and its derivatives of various orders.
 ordinary differential equation (ode) : not involve partial derivatives
 partial differential equation (pde) : involves partial derivatives
 order of the differential equation is the order of the highest derivatives
Examples:
 second order ordinary differential
equation
 first order partial differential equation
2
2
3 sin
d y dy
x y
dxdx
y y x t
x
t x x t

4. Terminologies In Differential
Equation
• Existence: Does a differential equation have a
solution?
• Uniqueness: Does a differential equation have more
than one solution? If yes, how can we find a solution
which satisfies particular conditions?
• A problem in which we are looking for the unknown
function of a differential equation where the values of
the unknown function and its derivatives at some point
are known is called an initial value problem (in short
IVP).
• If no initial conditions are given, we call the description
of all solutions to the differential equation the general
solution.

5. Differential Equations
Some Application of Differential Equation in Engineering

6. Linear Differential Equation
A differential equation is linear, if
1. dependent variable and its derivatives are of degree one,
2. coefficients of a term does not depend upon dependent
variable.
Example:
36
4
3
3
y
dx
dy
dx
yd
is non - linear because in 2nd term is not of degree one.
.0932
2
y
dx
dy
dx
ydExample:
is linear.
1.
2.

7. ( , )y f x y

8. First Order Linear Equations
• A linear first order equation is an equation
that can be expressed in the form
Where P and Q are functions of x

9. History
YEAR PROBLEM DESCRIPTION MATHAMATICIAN
1690 Problem of the
Isochrones
Finding a curve
along which a body
will fall with uniform
vertical velocity
James Bernoulli
1728 Problem of
Reducing 2nd Order
Equations to 1st
Order
Finding an
integrating factor
Leonhard Euler
1743 Problem of
determining
integrating factor for
the general linear
equation
Concept of the ad-
Joint of a differential
equation
Joseph Lagrange
1762 Problem of Linear
Equation with
Constant
Coefficients
Conditions under
which the order of a
linear differential
equation could be
lowered
Jean d’Alembert

10. Methods Solving LDE
1. Separable variable
M(x)dx + N(y)dy = 0
2. Homogenous
M(x,y)dx+N(x,y)dy=0, where M & N are nth degree
3. Exact
M(x,y)dx + N(x,y)dy=0, where M/ðy=0, where ðM/ðy = ðN/ðx

11. Solution of Differential Equation

12. 1st Order DE - Separable Equations
The differential equation M(x,y)dx + N(x,y)dy = 0 is separable if the equation can
be written in the form:
02211 dyygxfdxygxf
Solution :
1. Multiply the equation by integrating factor:
ygxf 12
1
2. The variable are separated :
0
1
2
2
1
dy
yg
yg
dx
xf
xf
3. Integrating to find the solution:
Cdy
yg
yg
dx
xf
xf
1
2
2
1

13. 1st Order DE - Homogeneous Equations
Homogeneous Function
f (x,y) is called homogenous of degree n if :
y,xfy,xf n
Examples:
yxxy,xf 34  homogeneous of degree 4
yxfyxx
yxxyxf
,
,
4344
34
yxxyxf cossin, 2  non-homogeneous
yxf
yxx
yxxyxf
n
,
cossin
cossin,
22
2

14. 1st Order DE - Homogeneous Equations
The differential equation M(x,y)dx + N(x,y)dy = 0 is homogeneous if M(x,y) and
N(x,y) are homogeneous and of the same degree
Solution :
1. Use the transformation to : dvxdxvdyvxy
2. The equation become separable equation:
0,, dvvxQdxvxP
3. Use solution method for separable equation
Cdv
vg
vg
dx
xf
xf
1
2
2
1
4. After integrating, v is replaced by y/x

15. 1st Order DE – Exact Equation
The differential equation M(x,y)dx + N(x,y)dy = 0 is an exact equation if :
Solution :
The solutions are given by the implicit equation
x
N
y
M
CyxF ,
1. Integrate either M(x,y) with respect to x or N(x,y) to y.
Assume integrating M(x,y), then :
where : F/ x = M(x,y) and F/ y = N(x,y)
ydxyxMyxF ,,
2. Now : yxNydxyxM
yy
F
,',
or : dxyxM
y
yxNy ,,'

16. 1st Order DE – Exact Equation
3. Integrate ’(y) to get (y) and write down the result F(x,y) = C
Examples:
1. Solve :
01332 3
dyyxdxyx
Answer:

17. Newton's Law of Cooling
• It is a model that describes, mathematically, the change in temperature of
an object in a given environment. The law states that the rate of change (in
time) of the temperature is proportional to the difference between the
temperature T of the object and the temperature Te of the environment
surrounding the object.
d T / d t = - k (T - Te)
Let x = T - Te
so that dx / dt = dT / dt
d x / d t = - k x
The solution to the above differential equation is given by
x = A e - k t
substitute x by T – Te
T - Te = A e - k t
Assume that at t = 0 the temperature T = To

18. T0 - Te = A e o
which gives A = To-Te
The final expression for T(t) is given by T(t) = Te + (To- Te) e - k t
This last expression shows how the temperature T of the object changes with time.

19. Growth And Decay
• The initial value problem
where N(t) denotes population at time t and k is a constant of proportionality,
serves as a model for population growth and decay of insects, animals and
human population at certain places and duration.
Integrating both sides we get
ln N(t)=kt+ln C
or
or N(t)=Cekt
C can be determined if N(t) is given at certain time.
)(
)(
tkN
dt
tdN
kdt
tN
tdN
)(
)(

20. Carbon dating
Let M(t) be the amount of a product that decreases withtime t and the rate of
decrease is proportional to the amount M as follows
d M / d t = - k M
where d M / d t is the first derivative of M, k > 0 and t is the time.
Solve the above first order differential equation to obtain
M(t) = Ae-kt
where A is non zero constant. It we assume that M = Mo at t = 0, then
M= Ae0
which gives A = Mo
The solution may be written as follows
M(t) = Mo e-kt

21. Economics and Finance
• The problems regarding supply, demand and compounding interest can be
calculated by this equation
is a separable differential equation of first-order. We can write it as
dP=k(D-S) dt.
Integrating both sides, we get
P(t)=k(D-S)t+A
where A is a constant of integration.
Similarly
S(t)=S(0) ert ,Where S(0) is the initial money in the account
)( SDk
dt
dP