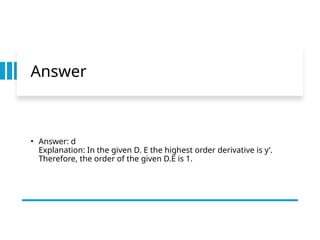
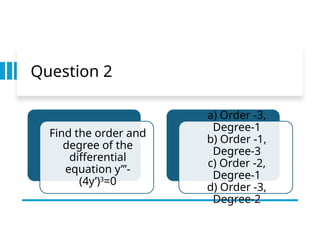
The document provides an overview of differential equations, covering definitions, classifications based on order and linearity, and solutions including general and particular forms. It explains concepts such as order, degree, homogeneous and linear differential equations, as well as the method to solve first-order linear differential equations. Additionally, it includes examples and questions to illustrate these concepts.

1. DIFFERENTIAL EQUATIONS
• An equation involving the Independent Variable
x, dependent Variable y and the differential
coefficients of dependent Variable with respect to
independent variable is called a Differential Equation

2. Order of a Differential Equation
• The Order of a Differential equation is the order of
the highest derivative occurring in the Differential
equation
• Eg : (i) + 2_
= 0
Order of the equation is 3
(ii) = 1 +
Order of the equation is 2

3. Degree of a Differential Equation
• The Degree of a Differential equation is the degree of the
highest derivative occurring in the Differential equation
• Eg : (i) + 2_
= 0
Degree of the equation is 1
(ii) = 1 +
Degree of the equation is 2
• Note: Order and degree (if defined) of a differential equation are always
positive integers.

4. Classifications of Differential Equation
• Classifications of Differential Equation
depends on their
(i) Order
(ii) Linearity

5. Classifications of Differential Equation
according to their Order
• First Order Differential Equation
First Order Differential Equation are those in
which only the First Order derivative of the
dependent variable occurs.
• Higher Order Differential Equation
Differential equations of order two or more
are referred as higher Order Differential Equation

6. Solution of a differential equation
A function which satisfies the given differential
equation is called its solution.

7. GENERAL AND PARTICULAR SOLUTIONS OF A
DIFFERENTIAL EQUATION
• The solution which contains arbitrary constants is called the
general solution (primitive) of the differential equation.
• The solution free from arbitrary constants i.e., the solution
obtained from the general solution by giving particular values
to the arbitrary constants is called a particular solution of the
differential equation.

8. Differential equation to form family of curves
• If the given family F1 of curves depends on only one
parameter then it is represented by an equation of the form
F1 (x, y, a) = 0
• If the given family F2 of curves depends on the parameters a,
b (say) then it is represented by an equation of the from
F2 (x, y, a, b) = 0

9. DIFFERENTIAL EQUATIONS WITH VARIABLES SEPARABLE
• If F (x, y) can be expressed as a product g (x) and h(y),
where, g(x) is a function of x and h(y) is a function of
y, then the differential equation = F(x,y) is said to be
of variable separable type.

10. HOMOGENEOUS DIFFERENTIAL EQUATIONS
• A function F(x, y) is said to be homogeneous function
of degree n if F(x, y) = n
F(x, y) for any nonzero
constant .
• A differential equation which can be expressed in the
form = f(x,y) or = g(x,y)
where f (x, y) and g(x, y) are homogenous functions of
degree zero is called a homogeneous differential
equation

11. LINEAR DIFFERENTIAL EQUATIONS
• A differential equation of the form
+ Py = Q, where P and Q are constants or
functions of x only is called a first order linear
differential equation.

12. Classifications of Differential Equation
according to their Linearity
• Linear and non-linear differential equations
A differential equation in which the
dependent variable and its derivatives occur
only in the 1st
degree and are not multiplied
together is called a Linear differential equation
otherwise it is non-linear.

13. Steps to solve first order linear differential
equation
(i) Write the given differential equation in the form + Py = Q where P,Q are constants
or functions of x only.
(ii) Find the Integrating Factor (I.F) =
(iii) Write the solution of the given differential equation as
y.(I.F) = x I.F) dx +C
Note: If the given differential equation is in the form + P1x = Q1 where P1,Q1 are
constants or functions of y only. Then I.F =
and the solution of the differential equation is given by x.(I.F) = x I.F) dy +C

14. Question 1
Find the order
of the
differential
equation y’-
20y+2=0.
a) 2
b) 8
c) 0
d) 1

15. Answer
• Answer: d
Explanation: In the given D. E the highest order derivative is y’.
Therefore, the order of the given D.E is 1.

16. Question 2
Find the order and
degree of the
differential
equation y”’-
(4y’)3
=0
a) Order -3,
Degree-1
b) Order -1,
Degree-3
c) Order -2,
Degree-1
d) Order -3,
Degree-2

17. Answer
• Answer: a
Explanation: In the D.E y”’-(4y’)3
=0, the highest order derivative is
y”’. Therefore, the order of the D.E is 3. Since it is a polynomial
equation, the degree will be the power raised to y”’. Therefore,
the degree is 1.

18. Question 3
Find the degree
of the
differential
equation y”-
12cosec y=0.
a) 1
b) 2
c) 4
d) Not defined

19. Answer
• Answer: a
Explanation: The highest order derivative in this D.E is y”. The
given D.E is a polynomial equation in y”. Therefore, the degree of
the D.E is the power raised to y” which is 1.

20. Question 4
Find the order and
degree of the
differential
equation 7y’-3y=0.
a) Order -1,
Degree-2
b) Order -2,
Degree-3
c) Order -1,
Degree-1
d) Order -3,
Degree-2

21. Answer
• Answer: c
Explanation: In the given D.E, the highest order derivative is y’.
Therefore, the order is 1. The given D.E 7y’-3y=0 is a polynomial
equation in y’ and the power raised to the highest derivative is 1.
Hence, the degree is 1.

22. Question 5
Find the order and
degree of the
differential
equation
(y”’)2
+7(y’)2
-
(cos⁡
x)2
=0
a) Order- 0,
Degree-2
b) Order- 3,
Degree-2
c) Order- 3,
Degree-3
d) Order- 1,
Degree-2

23. Answer
• Answer: c
Explanation: The highest order derivative in the equation is y”’.
Hence, the order is 3. The equation is polynomial in y”’.
Therefore, the degree of the D.E will be the power of the
derivative y”’ i.e. 2.