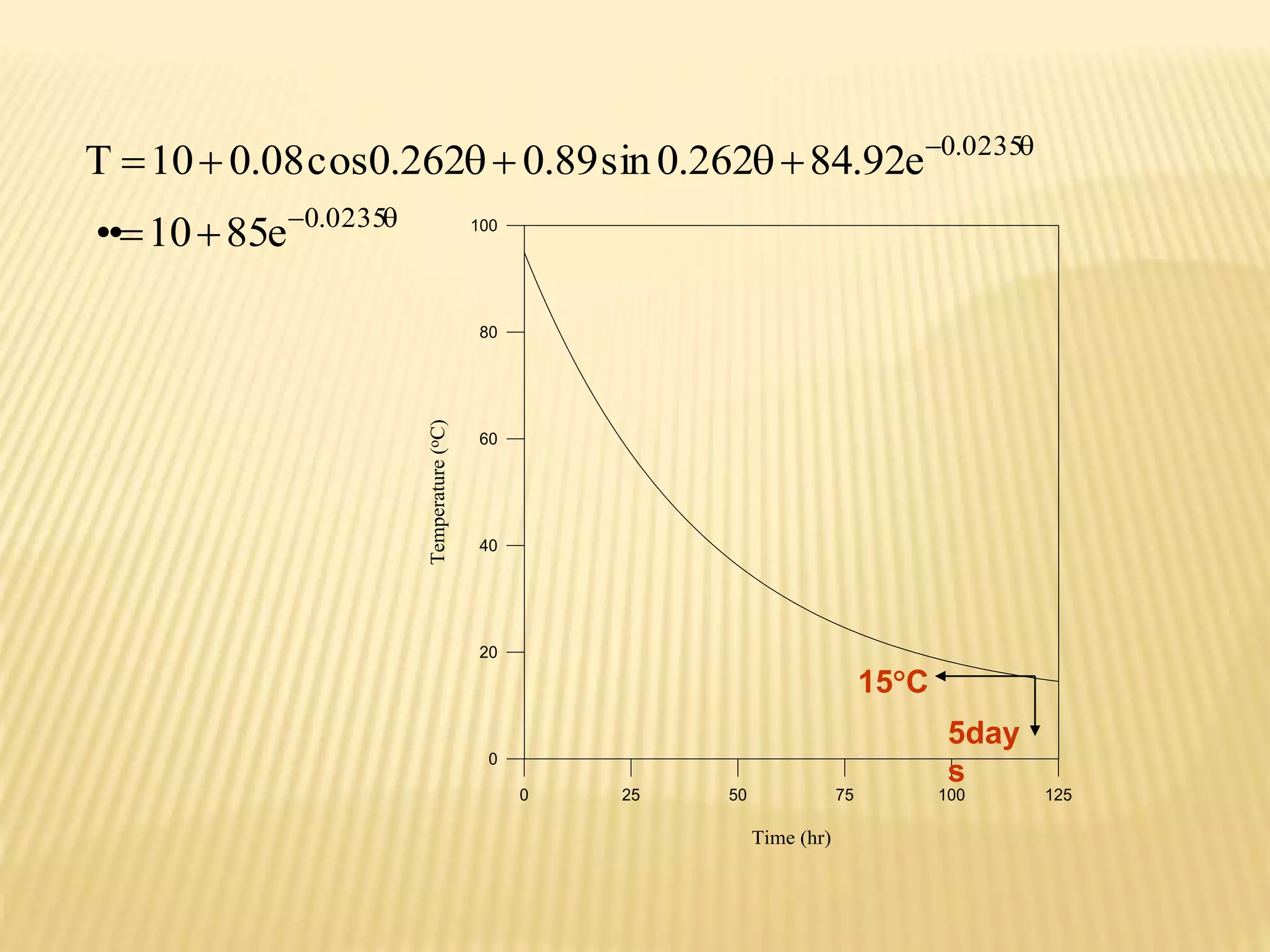
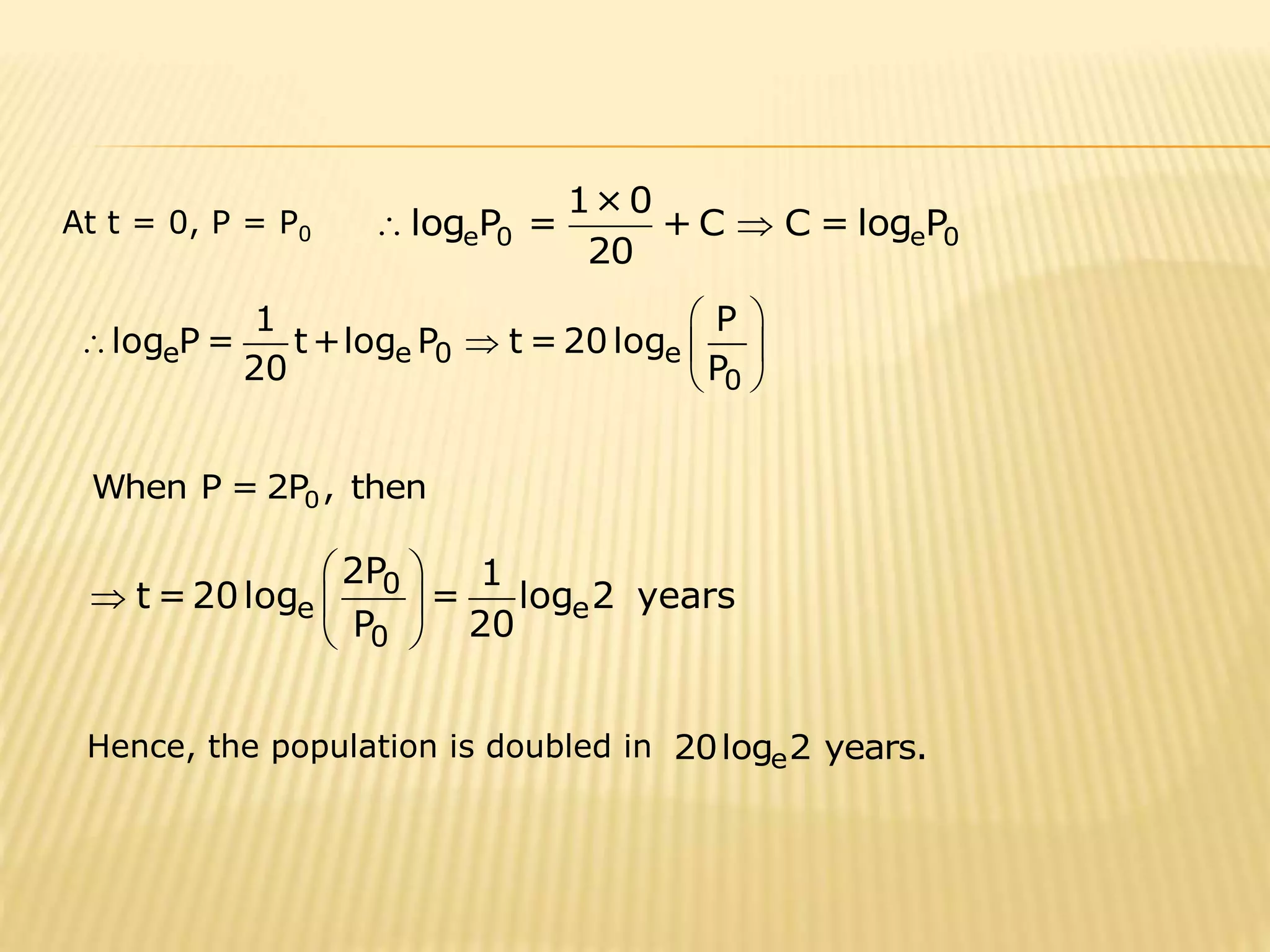The document describes how to calculate the time it takes for a population growing at 5% annually to double in size using a differential equation model. It is also solved to be 20loge2 years, or approximately 14 years. A second problem involves calculating the final temperature of liquid in an insulated cylindrical tank over 5 days using a heat transfer model. A third problem uses kinematics equations to find how far a drag racer will travel in 8 seconds if its speed increases by 40 feet per second each second.

2. A population grows at the rate of 5% per year. How long does it
take for the population to double? Use differential equation for it.
SOLUTION:- Let the initial population be P0 and let the population
after t years be P, then,
dP 5 dP P dP 1
 
   
 
= P = = dt
dt 100 dt 20 P 20
dP 1
= dt
 
P 20
e
1
log P= t+C
20

[Integrating both sides]

3. 1×0
log P = +C C =log P
At t = 0, P = P0 e 0 e 0
 
20
 
1 P
   
e e 0 e
0
log P= t+log P t=20log
20 P
 
0 When P =2P , then
2P 1
 
0
t=20log = log 2 years
  
e e
P 20
 0

Hence, the population is doubled in 20loge2 years.

4. An elevated horizontal cylindrical tank 1 m diameter and 2 m
long is insulated with asbestos lagging of thickness l = 4 cm,
and is employed as a maturing vessel for a batch chemical
process. Liquid at 95C is charged into the tank and allowed to
mature over 5 days. If the data below applies, calculated the
f i n a l t e m p e r a t u r e o f t h e l i q u i d a n d g i v e a
plot of the liquid temperature as a function of time.
Liquid film coefficient of heat transfer (h1) = 150 W/m2C
Thermal conductivity of asbestos (k) = 0.2
W/mC
Surface coefficient of heat transfer by convection and radiation (h2) = 10
W/m2C
Density of liquid () = 103 kg/m3
Heat capacity of liquid (s) =
2500 J/kgC
Atmospheric temperature at time of charging =
20C
Atmospheric temperature (t) t = 10 + 10 cos
(/12)

5. T
t
Ts
Tw
T represents the bulk liquid temperature
Tw represents the inside wall temperature of the tank
Ts represents the outside surface temperature of the
lagging
Area of tank (A) = ( x 1 x 2) + 2 ( 1 / 4  x 12 ) = 2.5 m2
Rate of heat loss by liquid = h1A (T - Tw)
Rate of heat loss through lagging = kA/l (Tw - Ts)
Rate of heat loss from the exposed surface of the lagging = h2A (TAt steady state, the three rates are equal:
kA
h A T T w w s s     
( ) ( ) ( ) 1 2 T T h A T t
l
k
k

h T   
w s T
l
h T
l


 1 1
kh

1 T t

T t s   
( )
h h l h k h k
1 2 1 2



 
 
T T t s  0.326  0.674

6. Considering the thermal equilibrium of the liquid,
input rate - output rate = accumulation rate
dT


d
h A T t V s s 0  (  )  2
0.072(0.326T 0.674t t)
dT
   

d
T t
dT
 0.0235  0.0235  0.235 0.235cos( /12)

d
integrating factor, e0.0235
         Te 0.235 e d 0.235 e cos( /12)d 0.0235 0.0235 0.0235
      0.0235 T 10 0.08 cos0.262 0.89 sin 0.262 Ke
B.C.  = 0 , T = 95 K=84.92

7. T  10  0.08cos0.262  0.89sin 0.262 
84.92e
 
 
 
0.0235
0.0235
•• 10 85e
0 25 50 75 100 125
Time (hr)
100
80
60
40
20
0
Temperature (oC)
5day
s
15C

8. A drag racer accelerates from a stop so that its speed
is 40t feet per second t seconds after starting. How far
will the car go in 8 seconds?
SOLUTION:-
40 t , wher s ( t
) is the distance in feet,
and t
is time in seconds.
ds
dt

s8 ? ft
Given:
Find:

9. t
ds
dt
 40
ds  40t dt
st   40 t dt  20
t 2 C Apply the initial condition: s(0) = 0
s 0  0  20  0
 2  C C  0
s  t   20t
2 8 208 1280 ft 2 s  
The car travels 1280 feet in 8 seconds.

10. Let population of country be decreasing at the rate
proportional to its population. If the population has
decreased to 25% in 10 years, how long will it take to
be half ?
SOLUTION:- This phenomenon can be modeled by
dN
Its solution is , N(t)=N(0) ekt ,
Where , N(0) in the initial population
For t=10, N(10)= (1/4)N(0)
kN(t)
dt


11. N(0) = (1/4)N(0) e10k
or
e10k= 1/4
or
k= (1/100 ln(1/4)
Set N(t)= (1/4) N(0)
(0)
1
t

N e N
2
1
ln
1
(0) 10
4
1
Or t=  8.3 years approximately
1
4
ln
1
10
2
ln