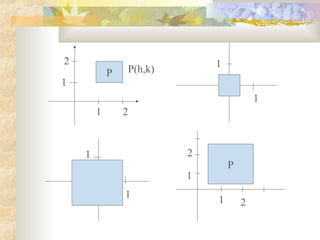
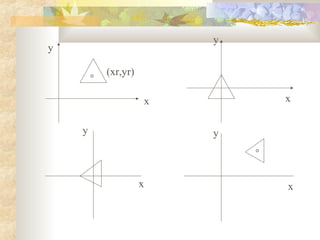
The document discusses how more complex geometric transformations can be performed by combining basic transformations through composition. It provides examples of how scaling and rotation can be done with respect to a fixed point by first translating the object to align the point with the origin, then performing the basic transformation, and finally translating back. Mirror reflection about a line is similarly described as a composite of translations and rotations.

1. Composite Transformation
More complex geometric & coordinate
transformations can be built from the basic
transformation by using the process of
composition of function.
Example: Scaling about a fixed point.
Transformation sequence to produce scaling
w.r.t a selected fixed position (h, k) using a
scaling function that can only scale relative to
the coordinate origin are:-

2. 2 1
P P(h,k)
1
1
1 2
1 2
P
1
1 1 2

3. Steps for doing composite transformation:-
1.) Translate the object so that its centre
concides with the origin.
2.) Scale the object with respect to origin.
3.) Translate the scale object back to the
original position.
Thus the scaling with respect to the point
can be formed by transformation.
S sx,sy , P = Tv . S sx,sy . Tv-1

4. Rotation about a fixed point
We can generate rotation about any selected
pivot point (xr,yr) by performing following
sequence of translate-rotate-translate opn.
1.) Translate the object so that pivot point
position is moved to the co-ordinate origin.
2.) Rotate the object about the co-ordinate
origin.
3.) Translate the object so that the pivot point
is returned to the original position.

5. y
y
(xr,yr)
x x
y y
x x

6. Thus the rotation about a point P can be
formed by the transformation
R θ ,P = Tv . Rθ . Tv-1
Mirror reflection about a line:
Let line L has a y intercept (0,b) & an angle of
inclination θ. Then the reflection of an object
about a line L needs to follow the following:
1.) Translate the intersection point to the
origin.

7. 2.) Rotate by -θ° so that line L align with x-
axis.
3.) Mirror reflect about the x-axis.
4.) Rotate back by θ°.
5.) Translate the origin back to the point (0,b).
y P’ L
(0,b) P
θ x

8. In translation notation, we have
ML = Tv Rθ Mx R-θ T-v
NoteWe must be able to represent the basic
transformation as 3x3 homogeneous
coordinate matrices so as to compatible with
the matrix of transformation. This is
accomplished by augmenting the 2 x 2 matrix
with the third column 0 i.e x y 0
0 a b 0
1 0 0 1

9. Ques1 What is the relation between Rθ, R -θ &
Rθ-1?
Ques2 (a) Find the matrix that represents
rotation of an object by 30° about the
origin.
(b) What are the new coordinates of the
point P(2,-4) after the rotation?
Ques3 Perform a 45° rotation of triangle
A(0,0), B(1,1), C(5,2) (a) about the origin
(b) about P(-1,-1).

10. Ques1 What is the relation between Rθ, R -θ &
Rθ-1?
Ques2 (a) Find the matrix that represents
rotation of an object by 30° about the
origin.
(b) What are the new coordinates of the
point P(2,-4) after the rotation?
Ques3 Perform a 45° rotation of triangle
A(0,0), B(1,1), C(5,2) (a) about the origin
(b) about P(-1,-1).