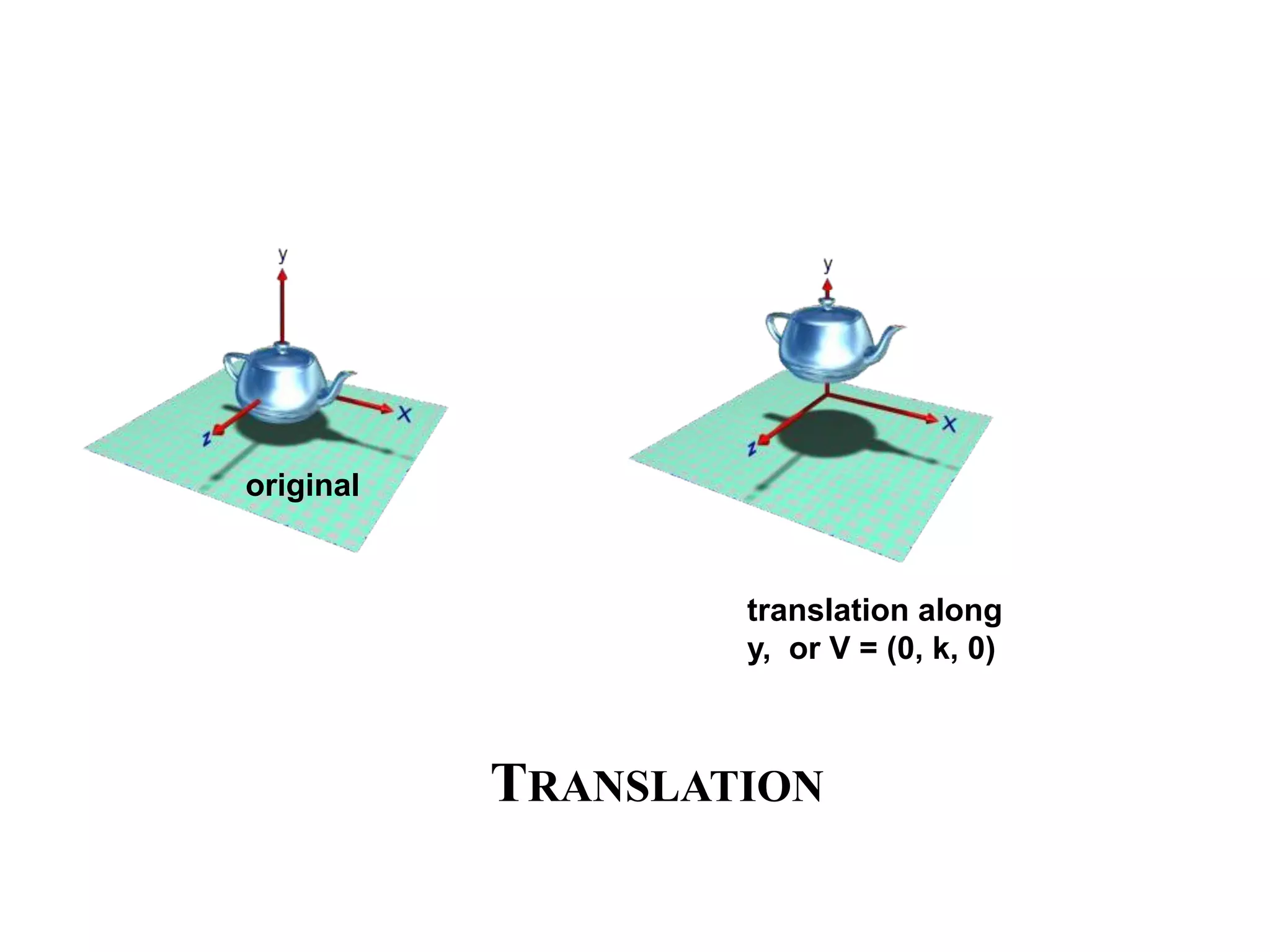
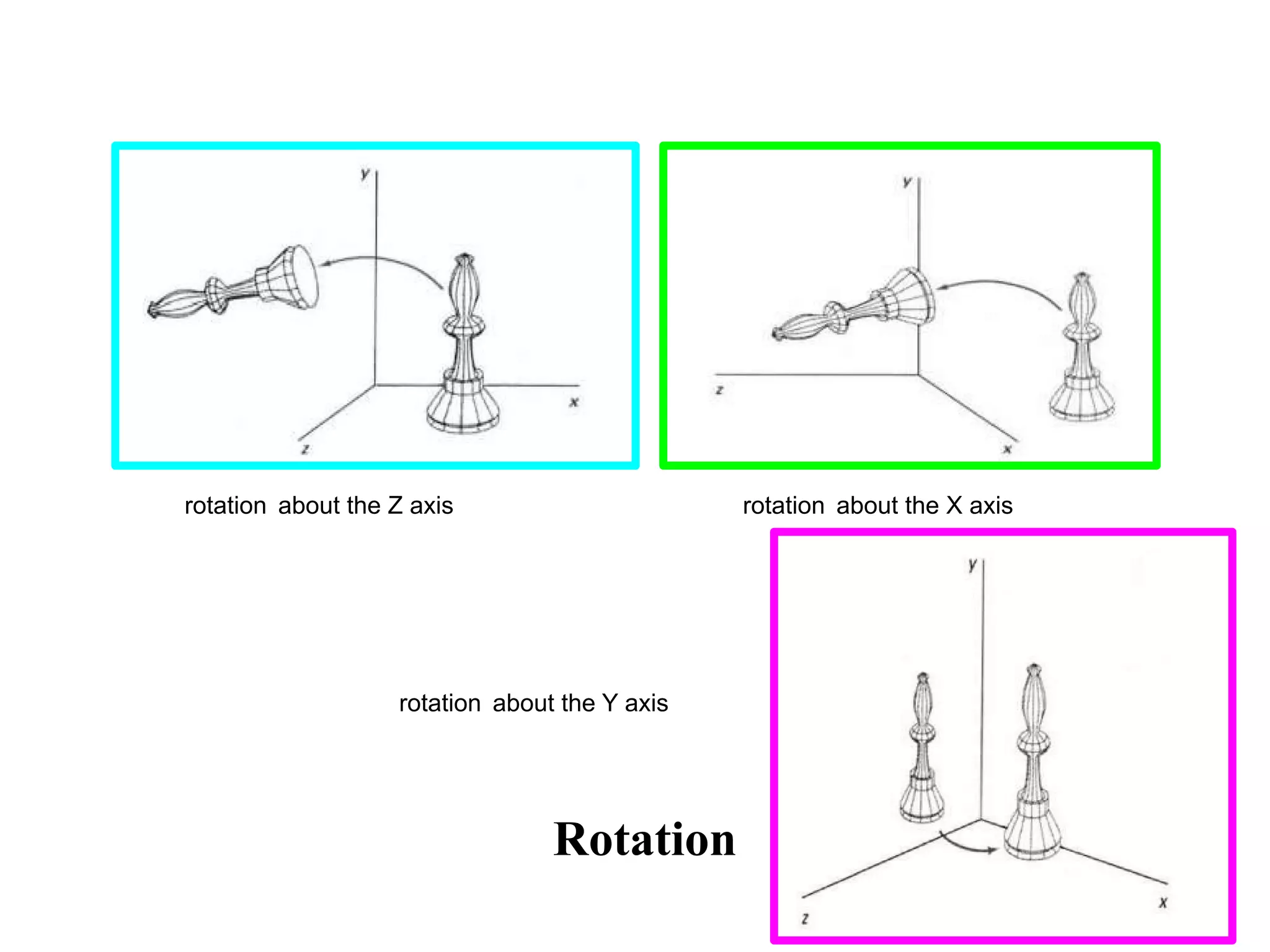
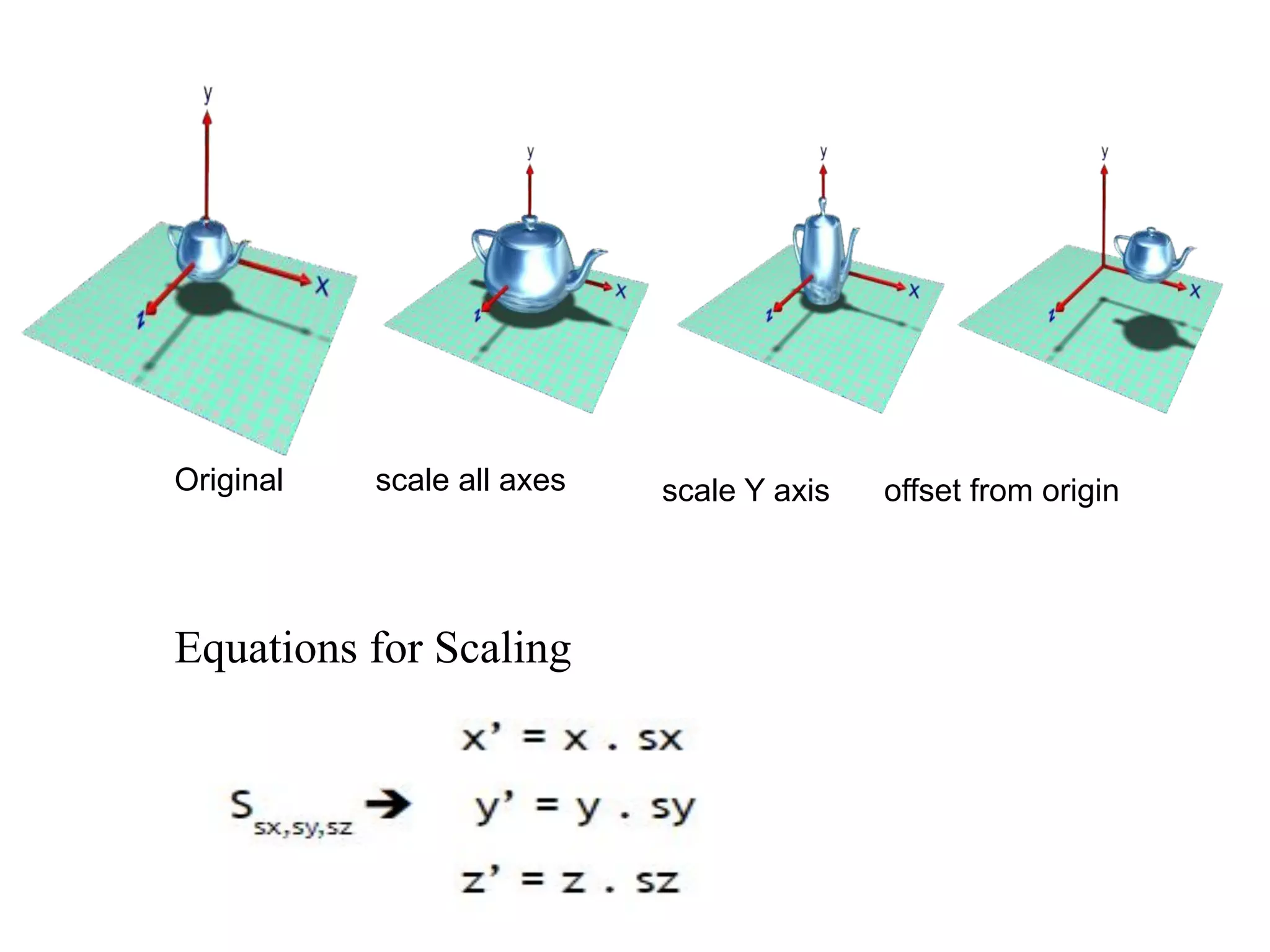
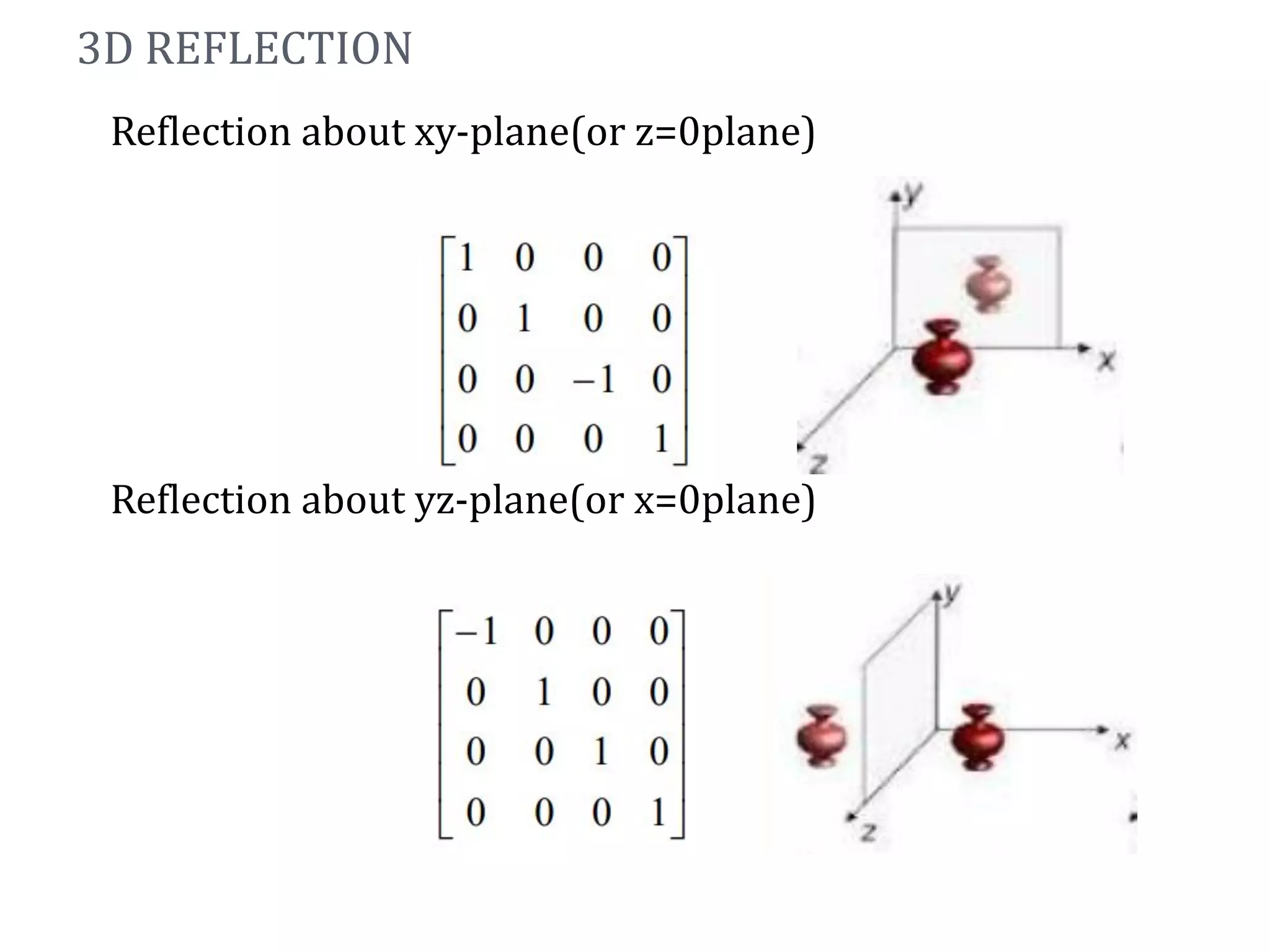
This document discusses various 3D transformations including translation, rotation, scaling, reflection, and shearing. It provides the transformation matrices for each type of 3D transformation. It also discusses combining multiple transformations through composite transformations by multiplying the matrices in sequence from right to left.

1. Computer Graphics
3D Transformation
CSE, MRIIRS

2. CONTENTS
● Transformation
● Types of 3-D Transformation
1) Translation
2) Rotation
3) Scaling
4) Reflection
5) Shearing

3. TRANSFORMATION
● Transformations are a fundamental part of the
computer graphics. Transformations are the
movement of the object in Cartesian plane .
● TYPES OF TRANSFORMATION
There are two types of transformation
in computer graphics.
○ 2D transformation
○ 3D transformation
● Types of 2D and 3D transformation
1)Translation 2) Rotation 3) Scaling
4) Shearing 5) reflection

4. 3D TRANSFORMATION
● When the transformation takes place on a 3D plane, it
is called 3D transformation
● The translation, scaling and rotation transformations
used for 2D can be extended to three dimensions.
● In 3D, each transformation is represented by a 4x4
matrix.
● Using homogeneous coordinates it is possible to
represent each type of transformation in a matrix
form and integrate transformations into one matrix
● To apply transformations, simply multiply matrices,
also easier in hardware and software implementation
● Homogeneous coordinates can represent directions

5. ● Homogeneous coordinates: 4 components
● Transformation matrices: 4×4 elements
● WHY WE USE TRANSFORMATION
Transformation are used to position objects, to shape
object, to change viewing positions, and even how
something is viewed.
1
⎥
⎢
0
⎥
r
⎥
⎢
⎢
q
⎥
⎢
d
p
⎡
a

6. 3D TRANSLATION
● Moving of object is called translation
● In 3 dimensional homogeneous coordinate
representation , a point is transformed from
position P = ( x, y , z) to P’=( x’, y’, z’)
● This can be written as: Using P’= T . P where
x'= x+tx , y'=y +ty , z'=z + tz;
● where tx,ty and tz are translational factors
⎥
⎥
⎥
⎢
⎥
⎢
1⎥
⎦
⎣
1
⎦
0
⎥
⎢
y
⎥
0⎤
⎡
x
⎤
0 0
1 0
0 1 0
⎥
⎢
z
⎥
ty
tz
⎢
⎢ ⎥
=
⎢
⎢ ⎥
⎢
0
⎢ ⎥
⎣
⎥
'
⎢
z
'
⎥
y
⎡
x
' ⎤
⎡
1
⎢
0
⎣
⎢
t
x

7. TRANSLATION
original
translation along
y, or V = (0, k, 0)

8. 3-D ROTATIONS
● Rotation needs an angle and an axis.
● Rotation is defined according to the right-hand
rule (our convention)
● In 3D, rotation is about a vector, which can be
done through rotations about x, y or z axes.
● Positive rotations are anti-clockwise, negative
rotations are clockwise, when looking down a
positive axis towards the origin
x
y
z
x
z
x
y y
z

9. 3-D ROTATION TRANSFORMATION MATRIX
Rotations are orthogonal matrices, preserving distances and
angles.
1. Rotation about X-axis
2. Rotation about Y-axis
3. Rotation about Z-axis
⎣ 1
⎥
⎥
0
⎥
⎢
0
⎢
0
0
⎥
0
⎤
⎡
1
⎢
0
0 0
cosθ sinθ
R x
=
⎢
⎦
⎢
⎢
⎣ 1
⎥
0
⎥
0
⎥
0
⎥
⎢
sin
θ
R y
=
⎦
1
⎥
⎥
0
⎥
0
0
0
⎥
⎢
− sinθ cosθ
R z
=

10. 3-D ROTATION TRANSFORMATION
1. Rotation about X-axis
2. Rotation about Y-axis
3. Rotation about Z-axis
⎣ 1
⎥
⎥
0
⎥
⎢
0
⎢
0
0
⎤
⎡
1
⎢
0
0 0
cosθ sinθ
⎦
⎢
⎢
⎣
0
⎥
0
⎥
0
⎥
⎦
1
⎥
⎥
0
⎥
0
0
0
⎥

11. rotation about the Z axis
Rotation
rotation about the X axis
rotation about the Y axis

12. 3-D SCALING
● You can change the size of an object using scaling
transformation .
● In the scaling process , you either expand or
compress the dimensions of the object .
● Scaling can be achieved by multiplying the original
coordinates of the object with scaling factor to get
the desired result
● The general transformation matrix for scaling is
⎥⎢ ⎥
⎦
⎥⎢ ⎥
0
⎥⎢
z
⎥
0
⎥⎢
y
⎥
0
⎤⎡
x
⎤
⎣
⎢ ⎥
= ⎢
⎢ ⎥
⎢
0
⎢
0
⎢
0
'
⎢
z
'
⎥
y
⎡
x
'
⎤
y

13. Scaling in x-direction by factor a
Scaling in y-direction by factor e
Scaling in z-direction by factor j
3-D SCALING
1
⎥
⎢
0
⎥
0
⎥
⎢
⎢
0
0
⎥
⎢
0
⎦
⎣ 1
⎥
⎢
0
⎥
0
⎥
⎢
⎢
0
0
⎥
⎢
0
⎦
0
⎤
0 0
⎦
⎣ 1
⎥
⎢
0
⎥
0
⎥
⎢
⎢
0
0
⎥
⎢
0

14. Scaling in x,y,z-direction by factor a,e,
j-units respectively.
Uniform scaling in x-direction by
factor a, if a>1 then expansion occurs if
0<a<1 contraction occurs
3-D SCALING
⎣ 1
⎥
⎢
0
⎥
0
⎥
⎢
⎢
0
0
⎥
⎢
0
1
⎥
⎢
0
⎥
0
⎥
⎢
⎢
0
0
⎥
⎢
0

15. Original scale all axes scale Y axis offset from origin
Equations for Scaling

16. 3D REFLECTION
● Reflection in computer graphics is used to emulate
reflective objects like mirrors and shiny surfaces
● Reflection may be an x-axis y-axis , z-axis. and
also in the planes xy-plane,yz-plane , and zx-
plane.
● Note: Reflection relative to a given Axis are
equivalent to 180 Degree rotations

17. Reflection about x axis
x’=x y’=-y z’=-z
Reflection about y axis
y’=y x’=-x z’=-z
3D REFLECTION
1
⎥
⎢
⎥
0
⎥
⎢
⎢
0
0
⎥
⎢
0
⎦
⎣ 1
⎥
⎢
0
⎥
0
⎥
⎢
⎢
0
0
⎥
⎢
0

18. Reflection about z axis
x’=-x y’=-y z’= z
3D REFLECTION
1
⎥
⎢
⎥
0
⎥
⎢
⎢
0
0
⎥
⎢
0
⎦
⎣ 1
⎥
⎢
0
⎥
0
⎥
⎢
⎢
0
0
⎥

19. Reflection about xy-plane(or z=0plane)
Reflection about yz-plane(or x=0plane)
3D REFLECTION
1
⎥
⎢
⎥
0
⎥
⎢
⎢
0
0
⎥
⎢
0
⎦
⎣ 1
⎥
⎢
0
⎥
0
⎥
⎢
⎢
0
0
⎥
⎢
0

20. Reflection about zx-plane(or y=0plane)
3D REFLECTION
⎦
⎣ 1
⎥
⎢
0
⎥
0
⎥
⎢
⎢
0
0
⎥
⎢
0
⎡
1 0 0 0
⎤
−1 0
0 1
0 0

21. 3D SHEARING
● Shearing is the process of slanting an object in 3D
space either in x, y, or in the z-direction. Shearing
changes(or deformed) the shape of the object.
⎥⎢ ⎥
1
⎦⎣
1
⎦
⎥⎢ ⎥
0
⎥⎢
z
⎥
0
⎥⎢
y
⎥
0
⎤⎡
x
⎤
⎢
⎣ ⎦
⎢
1
⎥
⎢
c
⎡
1 a b
1 d
⎢
e f 1
⎢ ⎥
=
⎢
⎢
z
′⎥
⎢
y′
⎥
⎡
x′
⎤
Shearing in x-direction
Here the coordinate of X remains unchanged while
the coordinate of Y and Z is changed.
x1 = x0
y1 = y0 + SHy. x0
z1 = z0 + SHz. x0

22. 3D SHEARING
Shearing in y-direction
Here the coordinate of Y remains unchanged while
the coordinate of X and Z is changed
Shearing in z-direction
⎣ 1
⎥
⎥
0
⎥
0
⎥
⎢
⎢
e
⎢
c
⎦
⎣ 1
⎥
⎢
0
⎥
0
⎥
⎢
⎢
0
0
⎥
⎢
0
x1 = x0 +SHx. y0
y1 = y0
z1 = z0 + SHz. y0
x1 = x0 +SHx. z0
y1 = y0+SHy. z0
z1 = z0

23. COMPOSITE TRANSFORMATION
A number of transformations or sequence of transformations can be combined into single
one called as composition.
The resulting matrix is called as composite matrix. The process of combining is called as
concatenation.
Suppose we want to perform rotation about an arbitrary point, then we can perform it by
the sequence of three transformations
1. Translation
2. Rotation
3. Reverse Translation
The ordering sequence of these numbers of transformations must not be changed. If a
matrix is represented in column form, then the composite transformation is performed by
multiplying matrix in order from right to left side. The output obtained from the previous
matrix is multiplied with the new coming matrix.

24. QUESTIONS
● How to rotate an object about an arbitrary axis
● How to shear along y and z axis
● Given a point P(90,20,40) perform rotation along
x axis by 45 degree,translation by tx=30 and
scaling sy=2 and find the final coordinate after
transformation