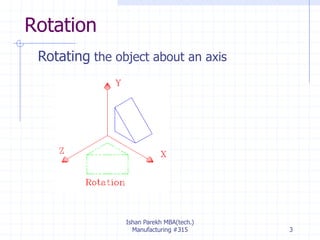
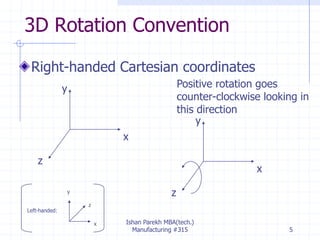
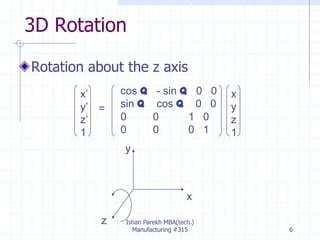
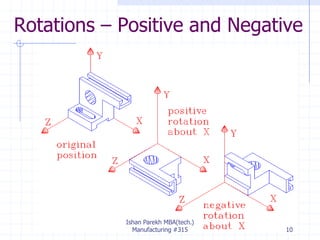
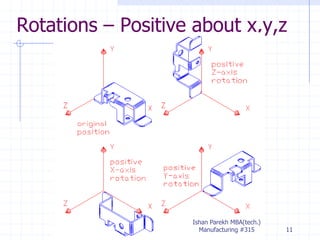
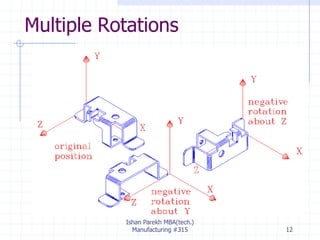
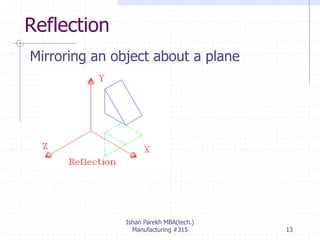
The document discusses 3D geometric transformations including rotation and reflection. It explains that transformations move points in space and can be expressed through 4x4 matrices. Specifically, it covers rotating objects around axes, conventions for right-handed vs left-handed systems, and how to perform rotations around arbitrary axes through a series of translations and rotations. It also discusses reflecting objects across planes by treating it as a scaling by -1 along one axis and provides AutoCAD commands for rotations and reflections.

1. 3D Geometric Transformations
Ishan Parekh MBA(tech.)
Manufacturing #315
Ishan Parekh MBA(tech.)
Manufacturing #315 1

2. Kinds of Transformations
Rotation
Reflection
• The process of moving points in space is called
transformation
• These transformations are an important
component of computer graphics programming
• Each transformation type can be expressed in a (4
x 4) matrix, called the Transformation Matrix
NOTES:
Ishan Parekh MBA(tech.)
Manufacturing #315 2

3. Rotation
Rotating the object about an axis
Ishan Parekh MBA(tech.)
Manufacturing #315 3

4. Rotation
Rotation is the process of moving a
point in space in a non-linear manner
it involves moving the point from one
position on a sphere whose center is at
the origin to another position on the
sphere
Rotation a point requires:
1) The coordinates for the point.
2) The rotation angles.
Ishan Parekh MBA(tech.)
Manufacturing #315 4

5. 3D Rotation Convention
Right-handed Cartesian coordinates
x
y
z
x
y
z
Positive rotation goes
counter-clockwise looking in
this direction
x
y
z
Left-handed:
Ishan Parekh MBA(tech.)
Manufacturing #315 5

6. 3D Rotation
Rotation about the z axis
cos q - sin q 0 0
sin q cos q 0 0
0 0 1 0
0 0 0 1
x’
y’
z’
1
x
y
z
1
=
x
y
z Ishan Parekh MBA(tech.)
Manufacturing #315 6

7. Rotation
Rotation about x-axis (i.e. in yz plane):
x′ = x
y′ = y cosθ – z sinθ
z′ = y sinθ + z cosθ
Rotation about y-axis (i.e. in xz plane):
x′ = z sinθ + x cosθ
y ′ = y
z′ = z cosθ – x sinθ Ishan Parekh MBA(tech.)
Manufacturing #315 7

8. 3D rotation around axis parallel
to coordinate axis
Translate object so that rotation axis
aligned with coordinate axis
Rotate about that axis
Translate back
Ishan Parekh MBA(tech.)
Manufacturing #315 8

9. 3D rotation around any axis
Translate object so that rotation axis passes through coordinate
origin
Rotate object so that axis of rotation coincides with coordinate axis
Perform rotation
Inverse rotate so that rotation axis goes back to original orientation
Inverse translate so that rotation axis goes back to original position
x
y
z
y’
x’
z’
(x0,y0,z0)
3D rotation around arbitrary axis:
Given: (x0,y0,z0) and vector v
Method:
(1) Let v be z’
(2) Derive y’ and x’
(3) Translate by (-x0,-y0,-z0)
(4) Rotate to line up x’y’z’ with xyz axes (see next
page), call this the rotation R.
(5) Rotate by q about the z axis
(6) Rotate back (R-1)
(7) Translate by (x0,y0,z0)
Ishan Parekh MBA(tech.)
Manufacturing #315 9

10. Rotations – Positive and Negative
Ishan Parekh MBA(tech.)
Manufacturing #315 10

11. Rotations – Positive about x,y,z
Ishan Parekh MBA(tech.)
Manufacturing #315 11

12. Multiple Rotations
Ishan Parekh MBA(tech.)
Manufacturing #315 12

13. Reflection
Mirroring an object about a plane
Ishan Parekh MBA(tech.)
Manufacturing #315 13

14. Reflection
A three-dimensional reflection can be
performed relative to a selected
reflection axis or with respect to a
selected reflection plane.
three dimensional
reflection matrices are set up similarly to
those for two dimensions.
Reflections relative to a given axis are
equivalent to 180 degree rotations.
Ishan Parekh MBA(tech.)
Manufacturing #315 14

15. 3D reflection
Let z-plane be the reflection plane
Comment: Reflection is like negative
scaling
Then, transformation matrix is:
1 0 0 0
0 1 0 0
0 0 -1 0
0 0 0 1
Ishan Parekh MBA(tech.)
Manufacturing #315 15

16. AutoCAD Transformation Commands
Geometric
Transformation
AutoCAD
Command
Rotation ROtate and ROTATE3D
Reflection MIrror and MIRROR3D
Ishan Parekh MBA(tech.)
Manufacturing #315 16

17. 3D Transformations
The End
Ishan Parekh MBA(tech.)
Manufacturing #315 17