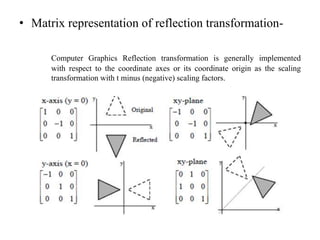
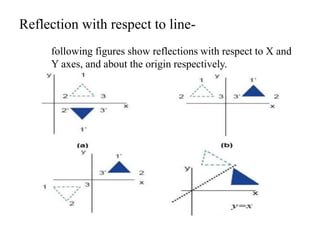
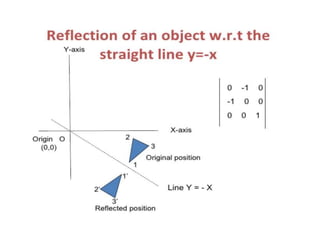
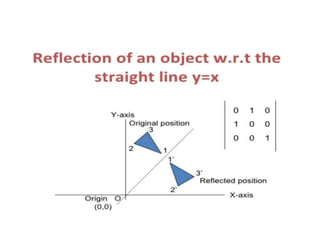
This document discusses reflection and composite transformations in computer graphics. Reflection is defined as a 180 degree rotation that produces a mirror image. There are two types of reflection: horizontal reflection across the y-axis and vertical reflection across the x-axis. A composite transformation performs two or more transformations sequentially, such as a translation followed by a reflection. Solving a composite transformation involves translating an object to rotate it around another point, applying the rotation, and translating back.

1. TOPIC –
ReflectionTransformation
And
CompositeTransformation

2. Reflection transformation
• Definition –
Reflection is the mirror image of original object. In other words, we
can say that it is a rotation operation with 180°.
In reflection transformation, the size of the object does not
change.
Basically the mirror image of any image for 2D reflection is
generated with respect to the “Axis of Reflection”. For that we need
to rotate main object 180 Degrees about the reflection axis.

3. Let us understand from this example-
As this image is reflecting with respect to the Y-axis, the reflection
transformation obviously keeps Y-values same. But one must notice
that, the image “Flips” 180 degrees and the values of X of coordinate
positions as shown figure. And similarly when the image gets reflected
with respect to X-axis. As mentioned in the above Y-axis case, the point
gets reflected with respect to Y-axis and obviously point gets flipped.

4. Types of reflection-
• Transformation in Computer Graphics Reflection is broadly classified in to
Two Categories. They are,
I. Horizontal Reflection II. Vertical Reflection
• I. Horizontal Reflection:
When Image gets flipped across, then the Image reflection is known ` as
Horizontal Reflection. And here image gets reflected with respect to the Y-
axis.
• II. Vertical Reflection:
When Image gets flipped up and down, the reflection is referred as Vertical
Reflection. For easy understanding, we are providing detailed image analysis,
which show both Horizontal and Vertical Reflections.

5. • Matrix representation of reflection transformation-
Computer Graphics Reflection transformation is generally implemented
with respect to the coordinate axes or its coordinate origin as the scaling
transformation with t minus (negative) scaling factors.

6. Reflection with respect to line-
following figures show reflections with respect to X and
Y axes, and about the origin respectively.

7. Composite Transformation
A composite transformation (or composition of
transformations) is two or more transformations performed one after
the other. Sometimes, a composition of transformations is equivalent
to a single transformation. The following is an example of a translation
followed by a reflection.
The original triangle is the brown triangle and the image is the
blue striped triangle. The brown striped triangle shows the
intermediate step after the translation has taken place.

8. Let us understand composite transformation with
this example-
• Example-
– Reflection through an arbitrary line.
we have already discussed reflection through the line x=0, y=0 and
y=x. All these lines passes through origin. But when reflection is to be
performed about a line that neither passes through the origin nor
parallel to the co-ordinate axis can be solved using the following steps-
Step 1- Translate the line and the object so that the line passes
through origin.
Step 2- Rotate the line and the object about the origin until the line is
coincident with one of the coordinate axis about which we are
familiar to perform reflection.
Step 3- Reflect the object through the co-ordinate axis.

9. Step 4- Apply the inverse rotation about the origin to shift the line
at translated position.
Step 5- Apply inverse translation to send back the object
(i.e., line) to its original position matrix rotation.
T = [TR ] * [Ro ] * [Rref] * [Ro
-1 ] * [Tr-1]
Where
TR - Translation matrix
Ro - Matrix for rotation by angle O
Rref – Reflection about any axis
R0
-1 - Inverse rotation
Tr
-1 - Inverse Translation

10. Reflection with respect to co-ordinate axis-

13. Example of solving an composite transformation
problem-
– we have already understand about rotation, which occurs
only about the origin but now our aim is to rotate the object
a point other than origin. For this purpose homogeneous
coordinate system will provide a method to accomplish
rotation about any point. This can be done in the following
order:
Step 1- Translate the object or body at the origin(i.e., translation)
Step 2- Rotate by any angle as given(i.e., Rotation)
Step3- Translate back to its original location(i.e.,
Inverse Translation)

14. • In matrix form, it can be shown as
[T] = [TR][RO][TR]-1
Where T
R = Translation matrix
R
O = Rotation matrix by an
angle 0
T
R
-1 = Inverse Translation
matrix