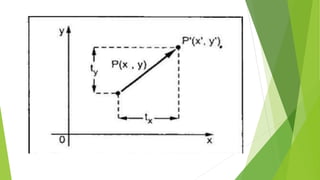
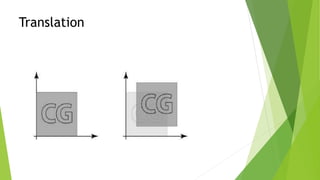
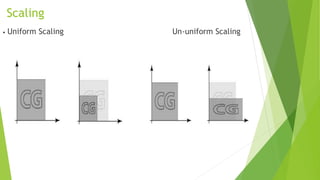
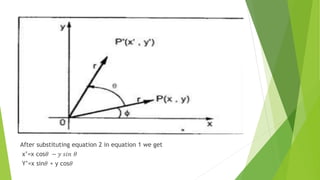
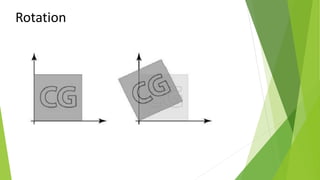
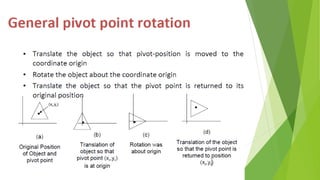
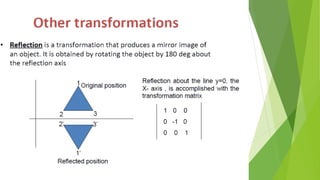
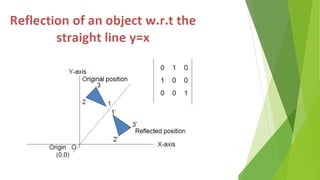
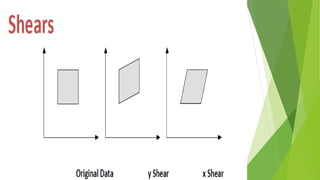
The document discusses 2D transformations in computer graphics, including translation, scaling, and rotation operations that alter an object's position, size, or orientation. It explains how to perform each transformation using mathematical formulas and matrix representations, with examples for translating and rotating points. The conclusion emphasizes the importance of transformations for manipulating and displaying modified objects efficiently.

1. 2D TRANSFORMATIONS
COMPUTER GRAPHICS

2. 2D Transformations
“Transformations are the operations applied to
geometrical description of an object to change its
position, orientation, or size are called geometric
transformations”.

3. Translation
 Translation is a process of changing the position
of an object in a straight-line path from one co-
ordinate location to another.
 We can translate a two dimensional point by
adding translation distances, tx and ty.
 Suppose the original position is (x ,y) then new
position is (x’, y’).
 Here x’=x + tx and y’=y + ty.

5. Translation

6. Homogeneous co-ordinates for Translation
 The homogeneous co-ordinates for translation are given as
T = 1 0 tx
0 1 ty
0 0 1
 Therefore , we have
x’ y’ 1 = x y 1 1 0 tx
0 1 ty
0 0 1

7.  Translate a polygon with co-ordinates A(2,5) B(7,10) and C(10,2) by 3
units in X direction and 4 units in Y direction.
 A’ = A +T
= 2 + 3 = 5
5 4 9
 B’ = B + T
= 7 + 3 = 10
10 4 14
 C’ = C + T
= 10 + 3 = 13
2 4 7

8. Scaling
 A scaling transformation changes the size of an object.
 This operation can be carried out for polygons by
multiplying the co-ordinates values (x , y) of each vertex
by scaling factors Sx and Sy to produce the transformed
co-ordinates (x’ , y’).
x’ = x . Sx
y’ = y . Sy
 In the matrix form
x’ y’ = x y Sx 0
0 Sy
= P . S

9. Scaling
• Uniform Scaling Un-uniform Scaling

10. Homogeneous co-ordinates for scaling
 The homogeneous co-ordinate for scaling are given as
S = Sx 0 0
0 Sy 0
0 0 1
 Therefore , we have
x’ y’ 1 = x y 1 Sx 0 0
0 Sy 0
0 0 1
= x . Sx y . Sy 1

11. Rotation
 A two dimensional rotation is applied to an object by
repositioning it along a circular path in the xy plane.
 Using standard trigonometric equations , we can express
the transformed co-ordinates in terms of 𝜃 𝑎𝑛𝑑 ∅ 𝑎𝑠
x’ = r cos(𝜙 + 𝜃) = 𝑟 cos𝜙cos𝜃 − r sin𝜙sin𝜃
y’ = r sin(𝜙 + 𝜃) = 𝑟 cos𝜙sin𝜃 + r sin𝜙co𝑠𝜃
 The original co-ordinates of the point is
x = r cos 𝜙
y = r sin 𝜙

12. After substituting equation 2 in equation 1 we get
x’=x cos𝜃 − 𝑦 𝑠𝑖𝑛 𝜃
Y’=x sin𝜃 + y cos𝜃

13. Rotation

14.  That equation can be represented in matrix form
x’ y’ = x y cos𝜃 𝑠𝑖𝑛𝜃
-sin𝜃 cos𝜃
 we can write this equation as,
P’ = P . R
 Where R is a rotation matrix and it is given as
R = cos𝜃 𝑠𝑖𝑛𝜃
-sin𝜃 cos𝜃

15.  A point (4,3) is rotated counterclockwise by angle of 45.
find the rotation matrix and the resultant point.
 R = cos𝜃 𝑠𝑖𝑛𝜃 = cos45 sin45
-𝑠𝑖𝑛𝜃 cos𝜃 -sin45 cos45
= 1/√2 1/√2
- 1/√2 1/√2
P’ = 4 3 1/√2 1/√2
- 1/√2 1/√2
= 4/√2 – 3/√2 4/√2 + 3/√2
= 1/√2 7/√2

16. Homogeneous co-ordinates for rotation
 The homogeneous co-ordinates for rotation are given as
R = cos𝜃 sin𝜃 0
-sin𝜃 cos𝜃 0
0 0 1
 Therefore , we have
x’ y’ 1 = x y 1 cos𝜃 sin𝜃 0
-sin𝜃 cos𝜃 0
0 0 1
= x cos𝜃 - y sin𝜃 x sin𝜃 + y cos𝜃 1

27. CONCLUSION
To manipulate the initially created
object and to display the
modified object without having to
redraw it, we use
Transformations.

28. THANK YOU