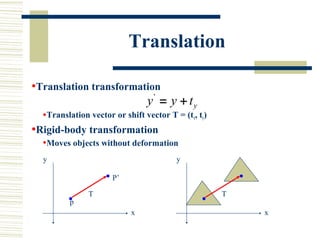
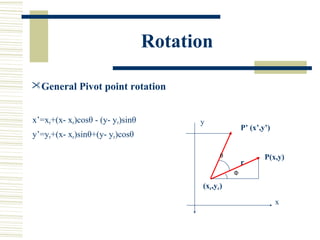
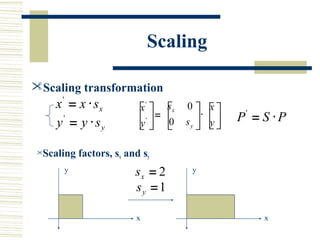
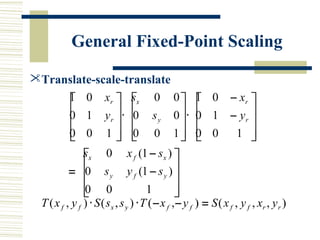
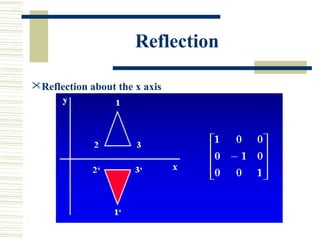
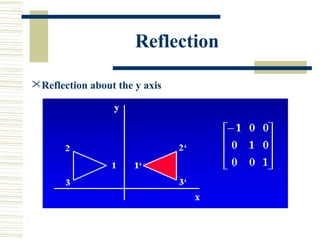
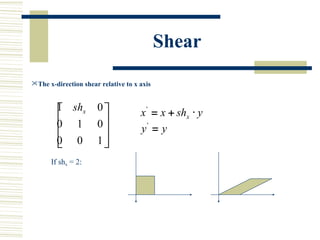
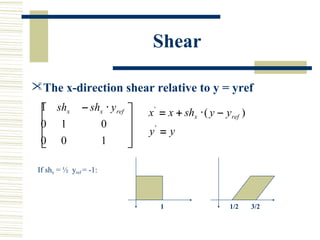
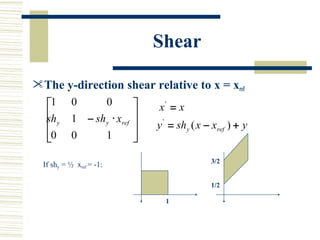
This document discusses various two-dimensional geometric transformations including translations, rotations, scaling, reflections, shears, and composite transformations. Translations move objects without deformation using a translation vector. Rotations rotate objects around a fixed point or pivot point. Scaling transformations enlarge or shrink objects using scaling factors. Reflections produce a mirror image of an object across an axis. Shearing slants an object along an axis. Composite transformations combine multiple basic transformations using matrix multiplication.

1. Two-Dimensional Geometric
Transformations

2. Two-Dimensional Geometric
Transformations
• Basic Transformations
• Translation
• Rotation
• Scaling
• Composite Transformations
• Other transformations
• Reflection
• Shear

3. Translation
•Translation transformation
•Translation vector or shift vector T = (tx, ty)
•Rigid-body transformation
•Moves objects without deformation
y y
P’
T T
p
x x

4. Rotation
Rotation transformation (anticlockwise)
x’=rcos(θ+Φ)= rcosθcosΦ - rsin θsinΦ
y’=rsin(θ+Φ)= rcosθsinΦ + rsin θcosΦ y
x=rcosΦ y=rsin Φ P’ (x’,y’)
x’=x cosθ - ysinθ
y’=xsinθ+ycosθ θ P(x,y)
r
Φ x
P’= R· P

5. Rotation
General Pivot point rotation
x’=xr+(x- xr)cosθ - (y- yr)sinθ y
P’ (x’,y’)
y’=yr+(x- xr)sinθ+(y- yr)cosθ
θ P(x,y)
r
Φ
(xr,yr)
x

6. Scaling
Scaling transformation
 Scaling factors, sx and sy
y y
x x

7. Scaling
 Fixed point

8. Matrix Representations and
Homogeneous Coordinates
•Homogeneous Coordinates
•Matrix representations
• Translation

9. Matrix Representations
 Matrix representations
 Scaling
 Rotation

10. Composite Transformations
Translations

11. Composite Transformations
Scaling

12. Composite Transformations
Rotations

13. General Pivot-Point Rotation
•Rotations about any selected pivot point (xr,yr)
•Translate-rotate-translate

14. General Pivot-Point Rotation

15. General Fixed-Point Scaling
Scaling with respect to a selected fixed position (x f,yf)

16. General Fixed-Point Scaling
Translate-scale-translate

17. Concatenation Properties
Matrix multiplication is associative.
A·B ·C = (A·B )·C = A·(B ·C)
Transformation products may not be commutative
 Be careful about the order in which the composite matrix is
evaluated.
 Except for some special cases:
Two successive rotations
Two successive translations
Two successive scalings
rotation and uniform scaling

18. Concatenation Properties
Reversing the order
 A sequence of transformations is performed may affect the
transformed position of an object.

19. Reflection
A transformation produces a mirror image of an object.
Axis of reflection
A line in the xy plane
A line perpendicular to the xy plane
The mirror image is obtained by rotating the object 180 0 about the
reflection axis.
Rotation path
Axis in xy plane: in a plane perpendicular to the xy plane.
Axis perpendicular to xy plane: in the xy plane.

20. Reflection
Reflection about the x axis

21. Reflection
Reflection about the y axis

22. Reflection
Reflection relative to the coordinate origin

23. Reflection
Reflection of an object relative to an axis perpendicular to the xy plane through P rfl

24. Reflection
Reflection about the line y = x

25. Shear
The x-direction shear relative to x axis
If shx = 2:

26. Shear
The x-direction shear relative to y = yref
If shx = ½ yref = -1:
1 1/2 3/2

27. Shear
The y-direction shear relative to x = xref
3/2
If shy = ½ xref = -1:
1/2
1