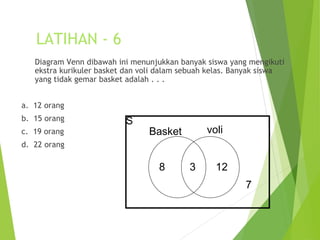
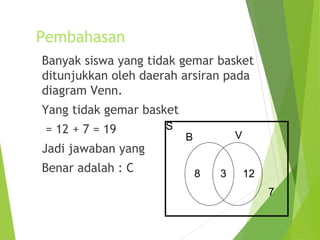
Dokumen tersebut merupakan silabus mata kuliah Matematika Keuangan dan Bisnis. Silabus tersebut menjelaskan tentang materi-materi yang akan diajarkan seperti himpunan, deret, matriks, fungsi linier dan non linier, serta penerapannya dalam masalah keuangan dan bisnis. Diuraikan pula tujuan pembelajaran, literatur yang digunakan, rencana penilaian, dan rincian sub materi yang akan dibahas.

1. NNAAMMAA :: AAGGUUSS DDWWII AATTMMOOKKOO,, SSEE,,
MMMM
AALLAAMMAATT :: DDss.. MMrreennttuull,, BBoonnoorroowwoo,,
1
KKeebbuummeenn
HHPP :: 00885522.. 99110011..55002277

2. Ruang Lingkup :
SILABUS
MATEMATIKA KEUANGAN DAN BISNIS
Himpunan, Permutasi dan Kombinasi, Deret, Matriks dan
Determinan, Anuiti dan Aplikasinya, Saham dan Obligasi,
Pembelian, Penjualan, Asuransi, Fungsi Linier, Penerapan
Fungsi Linier dalam Ekonomi Bisnis, Fungsi Non Linier,
Limit dan Kontinuitas, Turunan, Penggajian, Depresiasi,
Bunga dan Diskonto

3. Tujuan:
Mahasiswa diharapkan mampu memahami Konsep-konsep
Matematika dalam penerapannya pada
masalah Keuangan.
Kompetensi Lulusan:
Mampu menyelesaikan persoalan Matematika
permasalahan Keuangan, Ekonomi dan Bisnis.

4. Literatur
 1. Seri Diktat Kuliah Matematika Keuangan
Pengarang : - Algifari, Rudy Badrudin Penerbit :Gunadarma
 2. Seri Diktat Kuliah Matematika Ekonomi
Pengarang : Bambang Kustituanto, Penerbit : Gunadarma
 3. Matematika Dasar utk Perguruan Tinggi
Pengarang : - Yusuf Yahya, D. Suryadi H.S.
Penerbit : Ghalia Indonesia
 4. Matematika Terapan utk Bisnis&Ekonomi
Pengarang : Dumairy, Penerbit : BPFE - Yogyakarta
 5. Pengantar Matematika untuk Ekonomi
Pengarang : - Prof. H. Johannes
Budiono Sri Handoko, Penerbit : LP3ES

5. Rencana Penilaian
 Ujian Tengah Semester (UTS) 30 %
 Ujian Akhir Semester (UAS) 30 %
 Tugas Terstruktur 30 %
 Kuis 10 %

6. Materi
 Himpunan
 Permutasi dan Kombinasi
 Deret
 Matriks dan Determinan
 Anuiti dan Aplikasinya
 Saham dan Obligasi
 Pembelian, Penjualan
 Asuransi, Fungsi Linier, Penerapan Fungsi Linier dalam Ekonomi Bisnis,
Fungsi Non Linier, Limit dan Kontinuitas, Turunan, Penggajian, Depresiasi,
Bunga dan Diskonto

7. Silabus Materi Himpunan
 Pengertian Himpunan
 Penyajian Himpunan
 Himpunan Universal dan Himpunan Kosong
 Operasi Himpunan
 Kaidah Matematika dalam Operasi Himpunan

8. Silabus Materi Sistem Bilangan
 Hubungan Perbandingan antar Bilangan
 Operasi Bilangan
 Operasi Tanda
- Operasi Penjumlahan
- Operasi Pengurangan
- Operasi Perkalian
- Operasi Pembagian
 Operasi Bilangan Pecahan
- Operasi Pemadanan
- Operasi Penjumlahan dan Pengurangan
- Operasi Perkalian
- Operasi Pembagian

9. Silabus Materi Pangkat, Akar dan Logaritma
 Pangkat
 Kaidah pemangkatan bilangan
 Kaidah perkalian bilangan berpangkat
 Kaidah pembagian bilangan berpangkat
 Akar
 Kaidah pengakaran bilangan
 Kaidah penjumlahan bilangan terakar
 Kaidah perkalian bilangan terakar
 Kaidah pembagian bilangan terakar
 Logaritma
- Basis Logaritma
- Kaidah-kaidah Logaritma
- Penyelesaian Persamaan dengan Logaritma

10. Silabus Materi Deret
 Deret Hitung
- Suku ke-n dari DH
- Jumlah n suku
 Deret Ukur
- Suku ke-n dari DU
- Jumlah n suku

11. Silabus Materi Fungsi
 Pengertian dan Unsur- unsur Fungsi
 Jenis- jenis fungsi
 Penggambaran fungsi Linear
 Penggambaran fungsi non linear
- Penggal
- Simetri
- Perpanjangan
- Asimtot
- Faktorisasi

12. Silabus Materi Hubungan Linear
 Penggal dan lereng garis lurus
 Pembentukan Persamaan Linear
- Cara dwi- kordinat
- Cara koordinat- lereng
- Cara Penggal lereng
- Cara dwi- penggal
 Hubungan dua garis lurus
 Pencarian Akar- akar persamaan linear
- Cara substitusi
- Cara eliminasi
- Cara determinan

13. Silabus Materi Hubugan Non Linear
 Fungsi kuadrat
- Identifikasi persamaan kuadrat
- Lingkaran
- Elips
- Hiperbola
- Parabola

14. Silabus Materi Diferensial Fungsi Sederhana
 Kuosien Diferensi dan Derivatif
 Kaidah- Kaidah Diferensiasi
 Hakikat Derivatif dan Diferensial
 Derivatif dari Derivatif
 Hubungan antara Fungsi dan Derivatifnya
- Fungsi menaik dan fungsi menurun
- Titik ekstrim fungsi parabolik
- Titik ekstrim dan titik belok fungsi kubik

15. Silabus Materi Diferensial Fungsi Majemuk
 Diferensial Parsial
 Derivatif dari Derivatif Parsial
 Nilai ekstrim : Maksimum dan Minimum
 Optimisasi Bersyarat
- Pengganda Lagrange
- Kondisi Kuhn-Tucker
 Homogenitas Fungsi

16. Silabus Materi Integral
 Integral tak tentu
 Kaidah- kaidah Integrasi tak tentu
 Integral tertentu
 Kaidah- kaidah Integrasi Tertentu

17. Silabus Materi Matriks
 Pengertian Matriks dan Vektor
 Kesamaan Matriks dan Kesamaan
Vektor
 Pengoperasian Matriks dan Vektor
 Bentuk- bentuk khas matriks
 Pengubahan Matriks

18. 18

19. Himpunan (set)
 Himpunan (set) adalah kumpulan objek-objek yang
berbeda.
 Objek di dalam himpunan disebut elemen, unsur, atau
anggota.

20. Cara Penyajian Himpunan
 Enumerasi
 Simbol-simbol Baku
 Notasi Pembentuk Himpunan
 Diagram Venn

21. Enumerasi
adalah suatu set Konstanta Integer yang masing-masing
konstanta akan memiliki nama dan nilai yang berbeda
Contoh
- Himpunan empat bilangan asli pertama: A = {1, 2, 3, 4}.
- Himpunan lima bilangan genap positif pertama: B = {4, 6, 8, 10}.
-

22. Enumerasi
 Keanggotaan
x Î A : x merupakan anggota himpunan A;
x Ï A : x bukan merupakan anggota himpunan A.

23. Enumerasi
Contoh Misalkan: A = {1, 2, 3, 4},
R = { a, b, {a, b, c}, {a, c} }
K = {{}}
maka
3 Î A
5 Ï B
{a, b, c} Î R
c Ï R
{} Î K
{} Ï R

24. Enumerasi
Contoh
Bila P1 = {a, b}, P2 = { {a, b} }, P3 =
{{{a, b}}}
maka
a Î P1
a Ï P2
P1 Î P2
P1 Ï P3
P2 Î P3

25. Simbol-simbol Baku
P = himpunan bilangan bulat positif = { 1, 2, 3, ...}
N = himpunan bilangan alami (natural) = { 1, 2, ...}
Z = himpunan bilangan bulat ={...,-2, -1, 0, 1, 2,...}
Q = himpunan bilangan rasional
R = himpunan bilangan riil
C = himpunan bilangan kompleks

26. Simbol-simbol Baku
 Himpunan yang universal: semesta, disimbolkan dengan U.
 Contoh: Misalkan U = {1, 2, 3, 4, 5} dan
A adalah himpunan bagian dari U,
dengan A = {1, 3, 5}.

27. Notasi Pembentuk Himpunan
Notasi: { x ú syarat yang harus dipenuhi oleh x }
Contoh
(i) A adalah himpunan bilangan bulat positif yang kecil dari 5
A = { x | x adalah bilangan bulat positif lebih kecil dari 5}
atau
A = { x | x Î P, x < 5 }
yang ekivalen dengan A = {1, 2, 3, 4}
(ii) M = { x | x adalah mahasiswa yang mengambil kuliah MA
2333}

28. GABUNGAN HIMPUNAN
Gabungan himpunan A dan B adalah suatu himpunan yang
anggota-anggota nya menjadi anggota A saja atau anggota B
saja atau anggota persekutuan A dan B.

29. DDeennggaann nnoottaassii ppeemmbbeennttuukk
hhiimmppuunnaann,, ggaabbuunnggaann hhiimmppuunnaann AA
ddaann BB ddiiddeeffiinniissiikkaann sseebbaaggaaii ::
AA È BB == {{ xx || xx Î AA ddaann xx Î BB }}..

30. Contoh Soal
A = { m, e, r, a, h }
B = { r, a, t, i, h }
A È B = . . .
Penyelesaian : Semua anggota A dan B, tetapi anggota
yang sama hanya di tulis satu kali.
A È B = { m, e, r, a, h, i, t }

31. DIAGRAM VENN
Diagram Venn merupakan gambar himpunan yang digunakan
untuk menyatakan hubungan beberapa himpunan.

32. S
A

33. Model - 1
S
A , B
Jika anggota himpunan A sama
dengan anggota himpunan B
ditulis : A = B

34. Model 2
A B
S
Jika anggota himp. A tidak ada yang
sama dengan anggota himp. B
Ditulis : A ÉÌ B

35. Model - 3
S
A B
Jika ada anggota himpunan A juga
merupakan anggota himpunan B
Ditulis : A Ç B

36. Model 4
S
A
B
Jika semua anggota himpunan B
adalah anggota himpunan B
Dtulis : B Ì A

37. LATIHAN -1
S = { bilangan asli }, A = { bilangan ganjil }
B = { bilangan prima > 2 },
himpunan di atas dapat dinyatakan
dalam diagram Venn berikut :

38. S
A B
S
A B
S
A
B
S
B A
A
B
C
D

39. Pembahasan
S = { 1, 2, 3, 4, 5, . . . }
A = { 1, 3, 5, 7, 11, . . .}
B = { 3, 5, 7, 11, . . .}
Karena semua anggota himpunan B dimuat
di A maka B Ì A, artinya kurva B ada di
dalam kurva A.
Jadi jawaban yang benar adalah : C

41. LATIHAN - 2
Perhatikan gambar disamping
Yang bukan anggota K adalah . . .
a. { 7, 8 }
b. { 1, 2, 9 }
c. { 3, 4, 5, 6 }
d. { 1, 2, 7, 8, 9 }
S
.1 .2
K L
.3
.4
.5
.6
.7
.8
.9

42. Pembahasan
S
.1 .2
K L
.3
.4
.5
.6
S = { 1, 2, 3, . . ., 9 }
K = { 3, 4, 5, 6 }
Anggota S yang tidak
menjadi anggota K
adalah : { 1, 2, 7, 8, 9 }
Jadi jawaban yang benar adalah : D
.7
.8
.9

43. LATIHAN - 3
K = { k, o, m, p, a, s }
L = { m, a, s, u, k }
K È L = . . .
a. { p. o, s, u, k, m, a }
b. { m, a, s, b, u, k }
c. { p, a, k, u, m, i, s}
d. { k, a, m, p, u, s }

44. Pembahasan
K = { k, o, m, p, a, s }
L = { m, a, s, u, k }
K È L = { k, o, m, p, a, s, u }
Diantara jawaban A, B, C, dan D yang memiliki anggota = anggota K
È L adalah A
Jadi jawaban yang benar : A

45. LATIHAN - 4
P = { faktor dari 10 }
Q = { tiga bilangan prima pertama }
P È Q = . . . .
a. { 1, 2, 3, 4, 5, 7, 10 }
b. { 1, 2, 3, 4, 5, 10 }
c. { 1, 2, 3, 5, 7, 10 }
d. { 1, 2, 3, 5, 10 }

46. Pembahasan
P = { 1, 2, 5, 10 }
Q = { 2, 3, 5 },
maka :
P È Q = { 1, 2, 3, 5, 10 }
Jadi jawaban yang benar adalah : D

47. LATIHAN - 5
Jika himpunan A Ì B dengan n(A) = 11 dan n(B) = 18, maka n ( A Ç B
) = . . .
a. 7 b. 11
c. 18 d. 28

48. Pembahasan
n ( A ) = 11
n ( B ) = 18
Setiap A Ì B, maka A Ç B = A
Sehingga n ( A Ç B ) = n ( A )
n ( A Ç B ) = 11
Jadi jawaban yang benar adalah : B

49. LATIHAN - 6
Diagram Venn dibawah ini menunjukkan banyak siswa yang mengikuti
ekstra kurikuler basket dan voli dalam sebuah kelas. Banyak siswa
yang tidak gemar basket adalah . . .
a. 12 orang
b. 15 orang
c. 19 orang
d. 22 orang
S
Basket voli
8 3 12
7

50. Pembahasan
Banyak siswa yang tidak gemar basket
ditunjukkan oleh daerah arsiran pada
diagram Venn.
Yang tidak gemar basket
= 12 + 7 = 19
S
B V
Jadi jawaban yang
Benar adalah : C
8 3 12
7

51. LATIHAN - 7
Dalam sebuah kelas terdapat 17 siswa gemar matematika, 15
siswa gemar fisika, 8 siswa gemar keduanya. Banyak siswa
dalam kelas adalah . . .
a. 16 siswa c. 32 siswa
b. 24 siswa d. 40 siswa

52. Pembahasan
n(M) = 17 orang
n(F) = 15 orang
n(M Ç F ) = 8 orang
n( M È F ) = n(M) + n(F) – n(M Ç F )
= 17 + 15 – 8
= 32 – 8
= 24 orang
Jadi jawaban yang benar adalah : B

53. LATIHAN - 8
Dalam seleksi penerima beasiswa, setiap siswa harus lulus
tes matematika dan bahasa. Dari 180 peserta terdapat
103 orang dinyatakan lulus tes matematika dan 142 orang
lulus tes bahasa.

54. Banyak siswa yyaanngg ddiinnyyaattaakkaann lluulluuss
sseebbaaggaaii ppeenneerriimmaa bbeeaassiisswwaa aaddaa .. .. ..
aa.. 3388 oorraanngg cc.. 6655 oorraanngg
bb.. 4455 oorraanngg dd.. 7777 oorraanngg

55. Pembahasan
n(S) = 180 orang
n(M) = 103 orang
n(B) = 142 orang
n(M È B ) = x orang
n(S) = n( M È B ) = n(M) + n(B) – n( MÇB)
180 = 103 + 142 - X
X = 245 – 180 = 65
Jadi yang lulus adalah 65 orang = ( C )

57. LATIHAN-9
Dalam satu kelas terdapat 40 siswa,
12 orang di antaranya senang biola, 32
orang senang gitar, dan 10 orang
senang keduanya. Banyak siswa yang
tidak senang keduanya adalah….
a. 2 orang b. 4 orang
b. c. 6 orang d. 8 orang

58. Pembahasan
Biola = 12 orang, Gitar = 32 orang
Biola dan Gitar = 10 orang.
Jlh Siswa di kelas = 40 orang.
Jlh siswa = n(B) +n(G) – n( BÇG)
40 – x = 12 + 32 - 10
40 - x = 44 - 10
x = 40 – 34 = 6

59. LATIHAN - 10
Sebuah RS mempunyai pasien
sebanyak 53 orang, 26 orang menderita
demam ber- arah, dan 32 orang
menderita muntaber. penderita DBD dan
muntaber 7 orang,yang tidak menderita
DBD atau muntaber adalah …
a. 2 orang c. 5 orang
b. 3 orang d. 6 orang

60. Pembahasan
Jumlah pasien = 53 orang.
Demam berdarah = 26 orang.
Muntaber = 32 orang.
DBD dan muntaber = 7 orang.
Bkn DBD atau muntaber = X orang.
X = ( 53 org ) - ( 26 org + 32 org – 7 ) =
X = 53 org – 51 org
X = 2 orang

61. LATIHAN - 11
Dari 40 orang anak, ternyata 24 anak
gemar minum teh, 18 anak gemar minum
kopi, 5 anak tidak gemar minum
keduanya Banyaknya anak yang gemar
keduanya adalah . . .
a. 2 orang
b. 5 orang
c. 7 orang
d. 9 orang

62. Pembahasan
Jumlah anak = 40 orang
Teh = 24 orang
Kopi = 18 orang
Teh dan Kopi = x orang
Tidak keduanya = 5 orang
(24 + 18 ) - x = 40 - 5
42 - x = 35
x = 42 - 35 = 7
Yang gemar keduanya adalah 7 anak.

63. LATIHAN - 12
Dari 60 orang siswa ternyata 36 orang
gemar membaca, 34 orang gemar
menulis, 12 orang gemar kedua-duanya.
Banyaknya anak yang tidak mengemari
keduanya adalah . . .
a. 2 orang
b. 5 orang
c. 7 orang
d. 9 orang

64. Pembahasan
Jumlah anak = 60 orang
Membaca = 36 orang
Menulis = 34 orang
Membaca dan menulis = 12 orang
Tidak keduanya = x orang
(36 + 34 ) - 12 = 60 - x
58 = 60 - x
x = 60 – 58
x = 2.

65. LATIHAN - 13
Jika himpunan B Ì A dengan n(A) = 25
dan n(B) = 17, maka n ( A È B ) = . . .
a. 8 b. 11
c. 17 d. 25

66. Pembahasan
n ( A ) = 25
n ( B ) = 17
Setiap B Ì A,
maka A È B = A
Sehingga n ( A È B ) = n ( A )
n ( A È B ) = 25

67. LATIHAN - 14
Dalam sebuah kelas terdapat 20 siswa
gemar matematika, 15 siswa gemar
fisika, 8 siswa gemar keduanya.
Banyak siswa dalam kelas adalah . . . .
a. 23 siswa b. 27 siswa
b. c. 28 siswa d. 43 siswa

68. Pembahasan
n(M) = 20 orang
n(F) = 15 orang
n(M Ç F ) = 8 orang
n( M È F ) = n(M) + n(F) – n(M Ç F )
= 20 + 15 – 8
= 35 – 8
= 27 orang