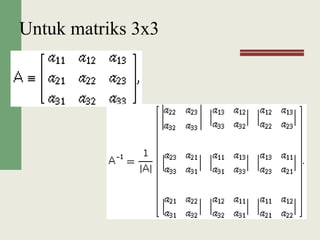
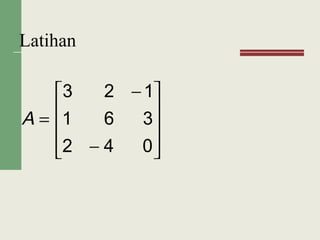
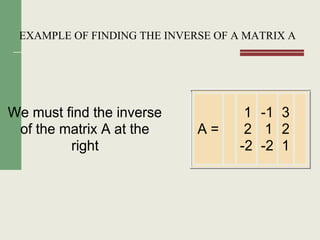
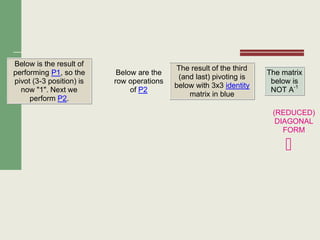
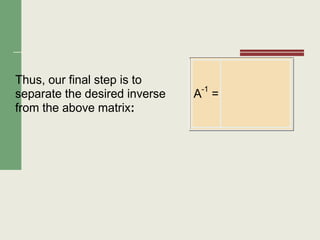
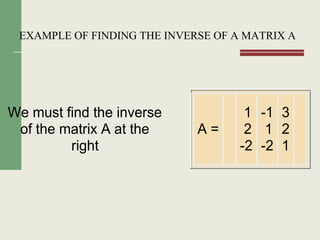
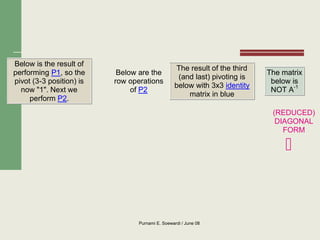
Matriks adalah susunan bilangan-bilangan yang diatur dalam baris dan kolom. Terdapat beberapa jenis matriks seperti matriks bujur sangkar, matriks diagonal, dan matriks identitas. Operasi yang dapat dilakukan pada matriks antara lain penjumlahan, pengurangan, perkalian skalar, dan perkalian matriks.





![Contoh :
−=
64
52
31
A
−
−
=
265
072
301
234
B
=
9
5
2
C
[ ]3249 −=D
[ ]6=E](https://image.slidesharecdn.com/matrik-140528114617-phpapp02/85/Matematika-Teknik-Matriks-6-320.jpg)
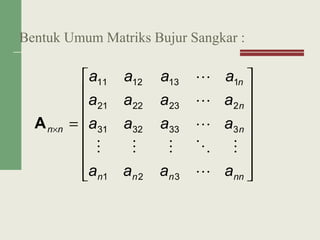
![Bentuk Umum Matriks :
[ ] nmijnm
mnmmm
n
n
n
nm
ij
a
aaaa
aaaa
aaaa
aaaa
nm
jia
nm
××× =
=
×
AA
AA
A
atau
:sebagaiditulisdanordomempunyaiMatriks.dari
kolomdanbarisdalamditerdapatyangentriadalahNotasikan
.kolomjumlahdanbarisjumlahmempunyaimatriksMisalkan
321
3333231
2232221
1131211
](https://image.slidesharecdn.com/matrik-140528114617-phpapp02/85/Matematika-Teknik-Matriks-7-320.jpg)












![Matriks yang semua entrinya sama dengan nol
Matriks NolMatriks Nol
[ ]0
0
0
0
0
0000
0000
000
000
000
00
00
111442 =
=
=
=
=
××× 000
00](https://image.slidesharecdn.com/matrik-140528114617-phpapp02/85/Matematika-Teknik-Matriks-22-320.jpg)





















![Contoh:
[ ]952
9
5
2
=⇔
= t
CC
[ ] [ ]66 =⇔= t
EE
−
−
=⇔
−
−
=
712
145
253
712
145
253
t
DD](https://image.slidesharecdn.com/matrik-140528114617-phpapp02/85/Matematika-Teknik-Matriks-44-320.jpg)