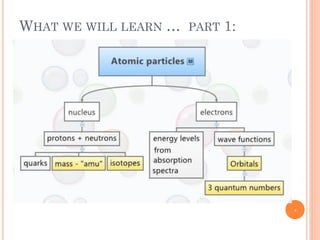
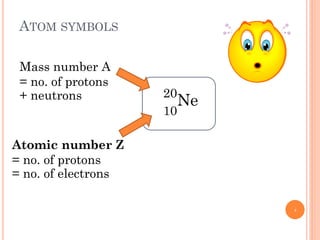
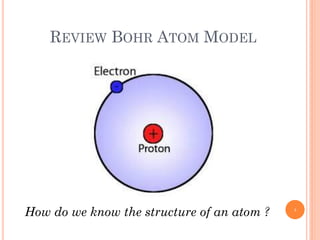
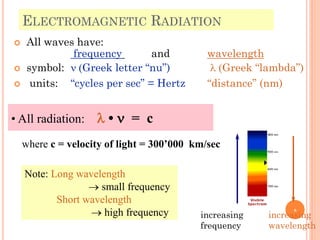
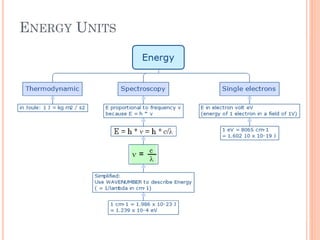
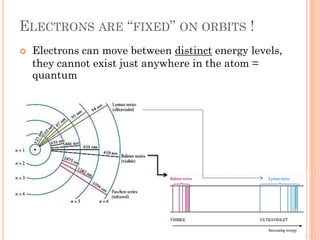
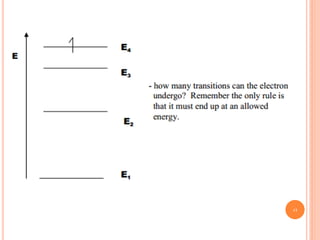
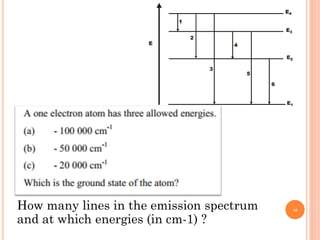
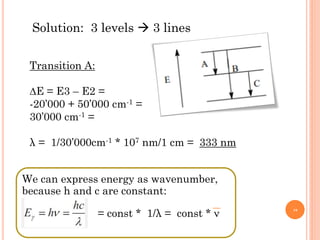
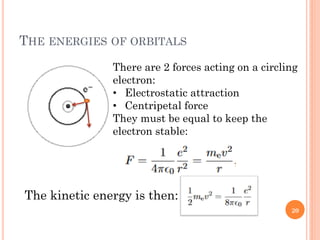
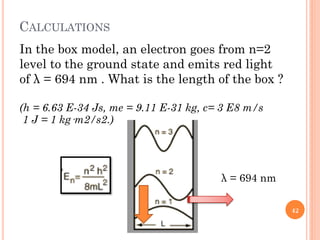
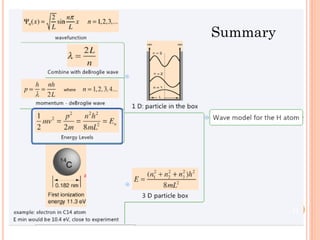
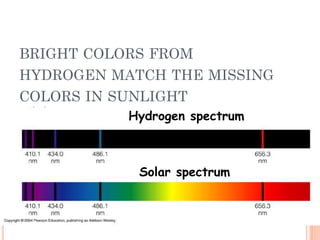
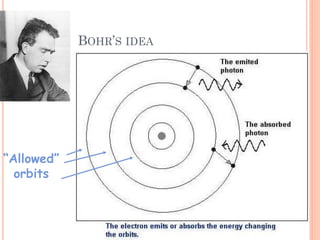
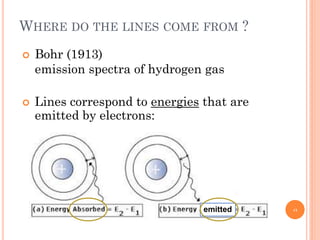
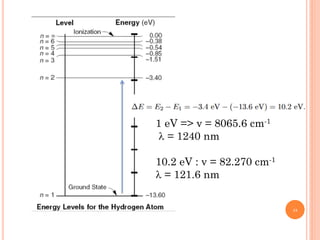
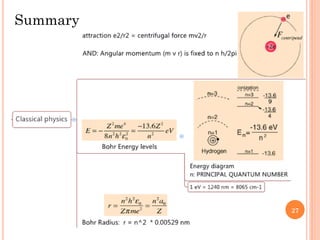
1) Electrons in atoms can only exist at certain discrete energy levels called quantum states. This is because electrons behave like waves and their wavelengths must fit within the boundaries of the atom. 2) Niels Bohr used this idea to explain the emission spectrum of hydrogen, showing electrons jumping between allowed orbits. 3) Later, the de Broglie hypothesis established that all particles like electrons exhibit both wave and particle properties. Treating electrons as waves led to the modern quantum mechanical model of atomic structure.

1. ATOMIC STRUCTURE
Lesson by Dr.Chris
University of Phayao, August 2016
1

2. WHAT WE WILL LEARN … PART 1:
2

3. ATOM SYMBOLS
Ne
20
10
Atomic number Z
= no. of protons
= no. of electrons
Mass number A
= no. of protons
+ neutrons
3

4. EXAMPLES
 How many protons, electrons and neutrons
are in:
4

5. SOLUTION
 Cl can have 18 or 20 neutrons
 35.45 is a mix of 2/3 35Cl and 1/3 37Cl
Element number
= no. of protons
= no. of electrons
Mass number, not integer !
=> mix of ISOTOPES with
different no. of neutrons !
Z
A
5

6. ISOTOPES
 Nearly all elements have isotopes,
that means the same elements
(no. of protons = Z) has different no. of
neutrons, and therefore different mass
 Example:
Copper exists to 69.2% of 63Cu and the rest
of 65Cu with masses 62.93 and 64.93
 what is the atomic mass of the mixture ?
6

7. REVIEW BOHR ATOM MODEL
How do we know the structure of an atom ? 7

8.  All waves have:
frequency and wavelength
 symbol: n (Greek letter “nu”) l (Greek “lambda”)
 units: “cycles per sec” = Hertz “distance” (nm)
• All radiation: l • n = c
where c = velocity of light = 300’000 km/sec
ELECTROMAGNETIC RADIATION
Note: Long wavelength
 small frequency
Short wavelength
 high frequency increasing
wavelength
increasing
frequency
8

9. Example: Red light has l = 700 nm.
Calculate the frequency n .
=
3.00 x 108
m/s
7.00 x 10-7
m
= 4.29 x 1014
Hzn =
c
l
• Wave nature of light is shown by classical
wave properties such as
• interference
• diffraction
ELECTROMAGNETIC RADIATION (2)
What is the energy in cm-1 ?
9

10. ENERGY UNITS
10

11. WHERE ARE THE ELECTRONS IN AN ATOM ?
 WE CAN KNOW FROM LIGHT SPECTRA !!
3 kinds of spectra:
11

12. BRIGHT COLORS FROM
HYDROGEN MATCH THE MISSING
COLORS IN SUNLIGHT
Hydrogen spectrum
Solar spectrum
12

13. Li
Na
He
K
Cd
H
A
B
C
D
Identify the elements in the mixture A – D !
13

14. BOHR’S IDEA
“Allowed”
orbits
14

15. WHERE DO THE LINES COME FROM ?
 Bohr (1913)
emission spectra of hydrogen gas
 Lines correspond to energies that are
emitted by electrons:
emitted 15

16. ELECTRONS ARE “FIXED” ON ORBITS !
 Electrons can move between distinct energy levels,
they cannot exist just anywhere in the atom =
quantum
16

17. 17

18. How many lines in the emission spectrum
and at which energies (in cm-1) ?
18

19. Solution: 3 levels  3 lines
Transition A:
∆E = E3 – E2 =
-20’000 + 50’000 cm-1 =
30’000 cm-1 =
λ = 1/30’000cm-1 * 107 nm/1 cm = 333 nm
We can express energy as wavenumber,
because h and c are constant:
= const * 1/λ = const * ν
19

20. THE ENERGIES OF ORBITALS
There are 2 forces acting on a circling
electron:
• Electrostatic attraction
• Centripetal force
They must be equal to keep the
electron stable:
The kinetic energy is then:
20

21. BOHR’S POSTULATE
A circling electric charge would emit energy, what is not
the case of real electrons.
Bohr postulated that electrons can live in certain energy
levels without loss of energy:
He assumed that the orbital angular momentum L = r *
p must be a multiple of h:
L = me * v * r = n * h/2 = n * h
21

22. From this we can calculate the orbital radius r:
with a0 as Bohr Radius
= 52.4 pm
-> the energy levels of the electron in a H atom are:
E1 = 13.6 eV
( 1eV = 8065.6 cm-1)
Calculate:
• an energy diagram for the H-atom electron
• the energy difference between the ground
and first excited state
• the wavelength of light emitted
22

23. 1 eV => v = 8065.6 cm-1
l = 1240 nm
10.2 eV : v = 82.270 cm-1
l = 121.6 nm
23

24. RYDBERG EQUATION
 From which energy level does an electron
come to n=2 when visible light of 410 nm
is emitted ?
 What is the Ionization energy of hydrogen
from this formula ?
-1
24

25. n = 2, RH = 1.0974 10-2 nm-1
 1/λ = 1.0974 10-2 * ( 1/4 – 1/n2) = 1/410
 1/n2 =1/4 - 1/(410 * 0.011)
 n2 = 36
=> n =6
The electron goes from n=6 to n=2 and
releases an energy that equals 410 nm
25

26. “HYDROGEN LIKE” ELEMENTS
The Bohr Theory can applied to all atoms
with one valence electron, like He(+)
Compare the energy of a transition
n=6  n=2
for H and He(+) in cm-1
http://www.fxsolver.com/browse/formulas/
Rydberg+formula+for+any+hydrogen-like+element
26

27. DETAILS
Summary
27

28. LESSON 2
QUANTUM THEORY:
THE ELECTRON AS A WAVE
28

29. WHY A NEW THEORY ?
The Bohr Theory could explain the nature of
the Hydrogen atom quite precisely
BUT: elements with more than one electron
could not be handled by this theory
AND: the classical theory cannot explain
why there are only certain orbits that are
“allowed” for electrons.
29

30. ELECTRON BEAM INTERFERENCE
 ELECTRONS SHOW WAVE-BEHAVIOUR !
For example, if two slits
are separated by 0.5mm
(d), and are illuminated
with a 0.6μm
wavelength laser (λ),
then at a distance of 1m
(z), the spacing of the
fringes will be 1.2mm.
n λ / d
d
30

31. ELECTRONS AS WAVES
DeBroglie: (“ de Broy “) 1924
The energy of a photon from Einstein’s
theory:
E = c * p = h *c / l
31

32. RELATION PARTICLE - WAVE
Means every moving particle can be
considered as wave.
In the macroscopic world, the wavelength is
so small that it is not measurable.
Example:
a gun projectile with m=10 g moves with
800 m/sec => what is its wavelength ?
Compare to an electron with m = 9.1 10-31 kg
(h = 6.626 x 10-34 J*s / 1J = 1 kg m2/s2) 32

33. CALCULATION
λ = (6.626 x 10^-34 J*s)/(0.01 kg)(800 m/s)
1 J = 1 kg*m^2/s^2
λ = 0.83 x 10^-34 m = 8.3 10-24 nm
(compare: x-ray around 1 nm)
But for an electron it is:
λ = (6.626 x 10-34 J*s)/(9 10-31kg)(800 m/s)
= 9.2 10-7 m = 920 nm similar red light 33

34. LIGHT WAVES = PHOTONS
When light is emitted (like from the sun or
a heated metal), the energy of the photons
is discrete - comes in “packets” of
E = h ν = h c/λ = m c2
Energy is not continuous, but quantisized !
(one quantum of energy is h ν )
34

35. EXPLAINS WHY ELECTRONS CAN ONLY
EXIST ON CERTAIN ORBITS
35

36. CONSEQUENCES: UNCERTAINTY !
When we treat electrons as waves, then we
cannot determine the position of the electron
exactly. The position (as particle) depends on
its speed – we describe this relation by the
Heisenberg Uncertainty Relation:
∆x m ∆v >= h/2π ( h )
(“Energy multiplied by time is constant”
Murphy’s Law)
36

37. ENERGY OF “WAVE-ELECTRONS”
 The model based on electrons circling
around a nucleus is not satisfying, even
it can explain the hydrogen atom.
 A new model based on
standing electron waves
was developed:
 Model the behaviour of a
particle in a restricted space
(“particle in a box”)
 Quantization comes from
the fact that a wave has
to “fit” into the boundaries
37

38.  Only wavelengths are allowed which “fit”
into the box length L:
 Use in DeBroglie:
(h = Planck constant)
 Therefore the kinetic energy is:
 n is the main quantum number
indicating the energy level 38

39. EXAMPLE
Calculate the first 2 energy levels for an
electron in a box with L = 300 pm (ca.
circumference of H-atom).
me = 9.1 * 10-31 kg h = 6.6 * 10-34 m2 kg/s
39

40. APPLICATION
The simple box model can help us to
estimate the color of linear chromophores
We can assume that 2 electrons
can move along this molecule
chain (“resonance”)
If C-C and N-C is 1.40 A, which
light will be absorbed by this
molecule ? 40

41. ANSWER
The molecule “length” is about 7 * 1.4 A
We have 8 electrons, the transition should
occur between level 5 and 4:
=> 352 nm
http://www.umich.edu/~chem461/Ex3.pdf
41

42. CALCULATIONS
In the box model, an electron goes from n=2
level to the ground state and emits red light
of λ = 694 nm . What is the length of the box ?
(h = 6.63 E-34 Js, me = 9.11 E-31 kg, c= 3 E8 m/s
1 J = 1 kg·m2/s2.)
λ = 694 nm
42

43. ANSWER
http://www.physics.umd.edu/courses/Phys270/Jenkins/Hwksolns13_Publishers.pdf
(compare: r(H) = 0.053nm => L is about the
double of the circumference )
43

44. SUMMARY
Summary
44